4415
Matematika feladatok
-
gregtom6 #3375 Azóta már rég megoldottam, csak még nem szántam arra időt, hogy ide leírjam a megoldást. De később le fogom. -
gregtom6 #3374 Hy all!
Itt egy feladat:
hanyadik permutációja az 12345-nek az 52341?
Ennek a megoldása 4!*4+3!*1+1*2!+1*1!+1=106.
A kérdésem, hogy miért van ez így kiszámolva? Tehát, h hogy kell megoldani egy ilyen feladatot. -
Pio #3373 Totál egyformának hat a két nagy háromszög mégis a ferde vonal a kis zöldeskék háromszögnél 0,4228, a pirosnál pedig 0,3936, ilyen minimális meredekségkülönbséget szabad szemmel nem igazán észlelünk, mégis ha az e miatti területkülönbség egy helyre összpontosul akkor már egyértelműen látható. -
Pio #3372 Felül a ferde vonalnál a meredekségek nem egyeznek. Amikor ott van a plusz üres rész, akkor nem látszik, mert nagyon nagy helyen oszlik el, amikor egy helyre összpontosul, akkor jól érzékelhető.
Itt van amúgy egy klasszikus ezen a trükkön alapuló "illúzió":
-
steweee #3371 gyóóóó, na erre vki vmit ?
http://video.boon.hu/onok-kuldtek/lehetetlen-puzzle_290_103300?autoPlay=true#ve_video_player_a
? -
 #3370
#3370
köszi szépen a segítséget! 

-
7th uwu #3369 Ja az lemaradt, hogy: a=gyök(1*a) -
7th uwu #3368 A mértani közép geometriai bizonyítása a megoldás.
Fel kell rajzolni a bizonyításkor használatos háromszögeket.
úgy hogy az /átfogó = a/ és a /kérdéses oldal merőleges vetülete = egység szakasz/
Ezt úgy lehet megszerkeszteni, hogy az "a" szakasz köré kört rajzolsz úgy hogy az "a" szakasz legyen az átmérő. Ráméred az egységet az "a" szakasz egyik végére, és merőlegest állítasz akol vége az egységszakasznak. Ahol metszi a kört összekötöd a szakaszok kezdőpontjával. Ez a szakasz a másik kettő mértani közepe, tehát a megoldás.
Ha "a" kisebb egynél ugyanezt kell csinálni, csak ki kell cserélni "a" és az egységszakasz szerepét.
Rajzolni sokkal könnyebb ám mint leírni... -
 #3367
#3367
Sziasztok, a hasonlósági transzformációkat tanuljuk és kaptam a házi feladatban egy olyan példát ami megakasztott:
"Adott egy egységnyi és egy a hosszúságú szakasz. Szerkesszen négyzetgyök alatt a hosszúságú szakaszt!"


-
gregtom6 #3366 Olvasgatom is, és a legtöbb feladatot meg is tudom oldani, csak van olyan, amikor máshogy gondolkodok, mint kellene.
A geometriai valószínűség számítás pl sokkal könnyebb a legtöbb esetben, mint a klasszikus. -
Pio #3365 Ezekhez az egyszerű, elemi valószínűségszámítási feladatokhoz az kell, hogy nagyon sok ilyet értelmezz, gondolj végig, láss, aztán már Neked is simán menni fog. Szerintem a gimis matek egyik legérdekesebb témája, mert nem mechanikusan kell képletekbe helyettesítgetni, mint szinte minden más témában (kivéve talán számelmélet és geometria, ha kell tanulatlan bizonyításokat csinálnotok), hanem szerephez jut a gondolkodás, a józan paraszti ész, ezen felül nem is teljesen haszontalan anyag (szerintem).
A lentebbi kömal-os link például nagyon hasznos olvasmány lehet a számodra. -
gregtom6 #3364 Na így már érthető.
Ettől függetlenül zavar az, h magamtól nem jöttem rá sem erre, se az előzőekre, amiket megkérdeztem. -
Pio #3363 Tossz=Rossz. :) -
Pio #3362 Tossz irányból gondolkodsz.
Teljesen lényegtelen, hogy melyik dominót tetted le az asztalra, azzal nem kell semmit számolni.
1-et kivettél a 45ből.
Maradt 44, amiből kiveszel egyet, ezt 44féleképp teheted meg.
Miért 9+9?
Mondok egy példát, hátha így érthetőbb lesz:
kitetted az asztalra mondjuk a 2|3-as dominót.
Mit fogsz tudni vele párba rakni?
2essel:
2|0
2|1
2|2
...
2|8
Ez 9 lehetőség
és
3|0
3|1
3|2
...
3|8
Ez újabb 9 lehetőség
Az összesen 9+9, DE a 2|3-at beszámoltuk 3|2-ként is, duplán számoltuk, ezért igazából 9+9-1 és ráadásul a 2|3-as dominó már kint is van az asztalon, tehát azt nem húzhatod, tehát 9+9-1-1=16.
És teljesen mindegy, hogy az asztalon 2|3, 5|1 vagy bármi más van, ez mindig ugyan így működik, ezért általánosítható az az eset, hogy az asztalon kint van egy nem dupla dominó és mellé akarsz húzni egyet.
Hogy miért 45 lapos?
Ehhez csak végig kell gondolni:
9féle jelölés lehet.
Dupla dominóból van összesen 9 darab.
Ez után mi marad? Példul 1-esnél:
1|0
1|2
1|3
...
1|8
Ez összesen 8 darab.
Ezt az összes számma eljátszhatom: 9×8=72.
Viszont így mondjuk az 1|4-est 4|1-esként is beszámolnám, tehát mindent 2szer számolok, szóval osztani kell 2-vel: 72/2=36.
Volt 9 dupla is, 36+9=45 -
Koppixer #3361 EZEN az oldalon nézd meg a 34. feladatot! Talán segít. -
gregtom6 #3360 Mondjuk fogalmam nincs, h hogy néz ki a 45 db-os dominókészlet. -
gregtom6 #3359 És miért 9+9?
Én kapásból arra gondolok, hogy
1. dominónál: 9*8 féle, egyik felén 0-8-ig, másik felén 1-el kevesebb, mivel nem duplikált.
2. dominónál: 1*8 féle, mivel 1féle szám lesz a másik dominón, amivel össze tud kapcsolódni, és 8 féle a másik oldalán, mivel nem duplikált.
és nem egyértelmű, hogy miért nem (45 2) az összes eset. -
Pio #3358 _Valószínűséget_ számolsz és nem esetszámot, tehát az eredmény egy 0, 1 közötti szám lesz.
Az 1 az az összes eset _valószínűsége_.
Kiszámolod a számodra nem kedvező esetek _valószínűségét_.
Ezt le kell vonnod az 1-ből, hogy megkapd a maradék eset (a számodra kedvező esetek) valószínűségét.
Dominó:
44 nyilván az összes maradék dominó száma, hisz azokból húzol 1 darabot, ami (44 1)=44 ez alapján 45 darabból áll a dominókészlet (8 pöttyös dominó), hisz egyet már kitettél és maradt 44.
A 16 pedig a lehetséges, kihúzható párok száma. 1 adott pötty összesen 9 különböző dominódarabon szerepel, ami 9+9=18 lehetőségnek tűnik, de nem annyi, mert ha a kihúzott dominón A és B pötty van, akkor azt beszámolnád A és B párjainál is, ami miatt valójában csak 17, ráadásul ezt a dominót már nem is húzhatod, hisz az asztalon van, ezért 16. -
gregtom6 #3357 Mert h szerintem az összes esetből kellene kivonni, és azt nem tudom, h hogy lehetne 1.
Más:
Dominójátszma kezdetén 1 dominót választunk, mely nem dupla, vagyis kétféle pont van a két felén. Ezután a többi dominóból egy második dominót választunk véletlenszerűen. Mi a valszege, h a 2. dominót az előzőhöz hozzá lehet tenni?
Na itt a megoldás 16/44 lenne, de nem jövök rá, h egyáltalán az összes eset hogy jön ki.
-
gregtom6 #3356 Új kérdés:
Egyszerre dobunk 6 szabályos dobókockával. Mi a valószínűsége annak, h legalább 2 dobókockán azonos pontszám lesz felül?
Ennek a megoldása 1-6!/6 a hatodikon.
Ez odáig világos, hogy a 6 a hatodikon az összes eset, és a szövegben leírt eset komplementere a 6!. De miért 1-ből vonjuk ki? -
gregtom6 #3355 Hát mondjuk ez igaz, triviális dolgot kérdeztem:) -
Pio #3354 Első feladat:
összesen hányféleképp húzhatsz: ismétlés nélküli variáció, ahogy írtad 9×10=90.
Jó esetek száma: 5 darab (18, 36, 54, 72, 90)
Valószínűség: 5/90=1:18
A második esetben nem számít, hogy milyen sorrendben rakod le a számokat, hisz ha a 2/4 egyszerűsíthető, akkor a 4/2 is.
Csak akkor lenne gond, ha köztük lenne a 0, de nincs.
Tehát összes eset:(8 2)=7×4=28
Jó esetek: a párosakból húzol kettőt, tehát (5 2)=2×5=10
Valószínűség: 10/28 -
gregtom6 #3353 Hy mindenki!
Van két valszegszám.-i feladat:
10 lapra felírunk 10 számjegyet. Határozzuk meg a valszegjét annak, h 2 lapot találomra kiválasztva és egymás mellé téve a kapott szám osztható 18-al?
Ennek az eredményében az összes eset 10*9 lesz.
Ez még oké, hisz gondolom itt azért van variáció, mert számít, h hogy rakom egymás mellé a lapokat(javítsatok ki, ha valahol tévednék).
8 azonos lapra egyenként felírjuk a köv. számokat:
2,4,6,7,10,11,12,13
Közülük 2 lapot találomra kiválasztok. Mi a valszegje annak, h a kiválasztott lapokon lévő számokat a tört számlálójának, illetve nevezőjének véve a tört egyszerűsíthető lesz?
Ennél a feladatnál meg nem értem az okát, hogy az összes esetet miért kombinációval oldották meg. Szerintem pedig itt se lenne mindegy, hogy hogy helyezem el a 2 számot....
Ha kiválasztás sorrendjében gondolkodok, akkor sem értem, hogy miért nem ugyanúgy variáció mind2 feladat összes esete...
Segítsetek pls. -
 #3352
#3352
köszönöm szépen! -
Pio #3351 Első:
(a+b)^3=a^3+3a^2b+3ab^2+b^3 alapján:
x^3+9x^2+27x+27-(x^3+6x^2+12^x+8)=19
Zárójelet eltüntetem:
x^3+9x^2+27x+27-x^3-6x^2-12^x-8=19
Összevonok bal oldalon:
3x^2+15x+19=19
Kivonok 19-et:
3x^2+15x=0
Bal oldalon kiemelek 3x-et:
3x(x+5)=0
Szorzat akkor nulla, ha valamelyik tényező 0.
A 3 nem lehet 0.
Az x akkor 0, ha x=0
az (x+5) akkor 0, ha x=-5
Két megoldás tehát:
x=0
x=-5
A másik is gondolom hasonló, ha nem megy szólj és végigírom. -
 #3350
#3350
(x+3)^3-(x+2)^3=19
(x-3)^3+2x(5x+1)=x^3-(2x-1)^2-26
nos az lenne a problémám, hogy mind a kettő feladatnál ha kiszámolom csak a 0 jön ki mint eredmény, és nem kapom meg a másik gyököt, valami ötlet? hogy mit rontok el? -
Kos7 #3349 Huh öregem hatalmas köszönet..kezdem érteni :D hnap irok ezekből szal te vagy a megmentő :D -
Pio #3348 Na, így van igazából értelme a felírásnak. :)
Eléggé hasonló a megoldás menete az előzőhöz.
Indulunk ezzel az azonossággal:
cos(a)×cos(b)=1/2×(cos(a-b)+cos(a+b))
a-nak az x/2-t veszem, hogy ne kelljen negatívokkal számolni.
ez alapján:
1/2×integral(cos(x/6)+cos(5x/6)dx
Ami szintén széttagolható, a zárójel felbontható::
1/2×(integral(cos(x/6))dx) + 1/2×(integral(cos(5x/6))dx)
cos-ban levő szorzó szintén reciprokként kivihető, megint nem részletezem:
a=x/6
b=5x/6
1/2×6×(integral(cos(a))da) + 1/2×6/5×(integral(cos(b))db))
Eltüntetjük az integrált, cos integrálja sinus, megjelenik a konstans tag, kiszámolom a szorzásokat:
3×sin(a) + 3/5×sin(a) + C
visszahelyettesítek:
3×sin(x/6) + 3/5×sin(5x/6) + C -
Kos7 #3347 -
Kos7 #3346 igy van az egész -
 #3345
#3345

-
Kos7 #3344 bocs.. így
-
Pio #3343 rajzold le paintben... :D -
Pio #3342 Tehát felül cos négyzet x alul pedig 6? Vagy csak rosszul tördelődött? :)
Gyanús, hogy az osztások csak az x-re vonatkoznak, mert semmi értelme nem lenne annak, hogy felül szétírják a cos négyzetet alul pedig a 6-ot. :) -
Kos7 #3341 cos x * cos x
- -
2 3 -
Pio #3340 Itt a /2 az az x alatt van vagy az egész cosx alatt?
Tehát cos(x)/2 vagy cos(x/2)?
És persze ugyan ez a kérdésem a /3ról is. :) -
Kos7 #3339 Hű köszi a segítséget..viszont ehhez kapcsolodóan van még gondom :D van egy olyan is hogy integrál cosx/2*cosx/3 dx = ... -
Pio #3338 Van egy ilyen azonosság, hogy:
sin(a)×cos(b)=1/2×(sin(a-b)+sin(a+b))
Ez alapján átírható:
integral((1/2×(sin(8x)-sin(2x)))dx)
Konstans tag kiemelhető:
1/2×integral((sin(8x)-sin(2x))dx)
Integrálon belüli kivonás szétbontható:
1/2×(integral((sin(8x))dx)-integral((sin(2x))dx))
sin-ben levő szorzó törtként kívülre hozható ez alapján:
integral((sin(2x)dx)=1/2×integral((sin(a)da)
a=8x
b=2x
1/2×(1/8×integral((sin(a))da)-1/2×integral((sin(2b))db))
A sinusnak pedig már tudjuk az integrálját, illetve a zárójelet is felbontjuk és megjelenik a konstans tag:
1/16×(-cos(a))-1/4×((-cos(b)) + C
Visszahelyettesítés, előjelek rendezése, pozitív tag előrehozása:
cos(2x)/4 - cos(8x)/16 + C -
Kos7 #3337 Légyszives segítsetek...:S integrálni kéne ezt .. *integráljel*sin3xcos5x dx=....egyszerűen nem tudom mi alapján van..hiányoztam óráról és nem tudom... -
 #3336
#3336
akkor elirtam vagy tanarom hulye :D


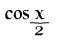 így
így