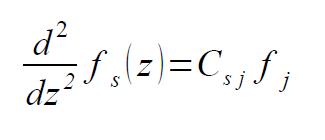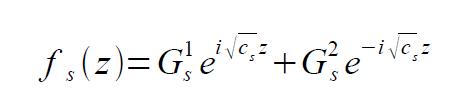4415
Matematika feladatok
-
acosz85 #3255 Sziasztok!
Az élet adott egy feladatot amit ki akartam számolni de hülyeséget kaptam így ide fordulok!
Egy derékszögű háromszög egyik szöge 2,5° a mellette lévő oldal 4600 mennyi a szembelévő oldal?
Én ezt úgy próbáltam kiszámolni, hogy tg2,5 x 4600-al de annak az eredménye 3435 ami nem lehetséges!
Ezt a tg alfa = szög szemközti/szög melletti befogó képletből számoltam ki.
-
lally #3254 Sejtettem, hogy Harmadikas vagy, és a pótvizsgádra készülsz a napokban!
-ha kimondottan számítással kérik megoldani a hasonló feladatot,
ilyen profi_SKICC akkor is kell! -mert ez nélkül; Nem is megy !.
(1 percen belül kész, és a példádra így már kapsz eleve KETTESt !
A kiszámolása, még a profiktól is legalább 5-6 percet igényel.)
Az alábbi képletek Kellenek:
-1; A kétponton átmenő egyenes egyenlete:
y -y1= m (x -x1) ;;; ahol az
m= (y2-y1)/(x2-x1) ;;; m= az egyenes iránytangense, azaz a Meredeksége.
Válasszuk az most "A"-pontot 1.indexre, "B" pedig legyen a 2.jelű.
(X és Y , a kötelező betűk !)
Tehát:
x1=8 ; y1=5
x2=2; y2=7
Ezeket most Te helyettesítsd be, és oldd meg, azaz rendezd ki
y= ...
(Várom az eredményt!) -aztán:folyt, köv.
-
 #3253
#3253
Csak az a baj hogy ebbe pótvizsgán belekötnek :D de már megértettem sikerült kiszámolni, de köszönöm szépen a tippet :) -
lally #3252 De: Neked, az adott középpont koordinátáját kell megadnod. -igaz ?
A szerkesztés pedig; Éppen olyan pontos megoldást is adhat, mint a számolás!
-csak az Optimális_"Lépték-megválasztása" okozhat benne kisebb gubancot.
(Ehhez kell majd a nagyobb gyakorlat.)
Fogj tehát egy "A4" (azaz: 210 * 297mm)-es lapot először, és hajtsd félbe.
10mm (= 1,0 cm) legyen most 1 hosszegységed. Így vedd fel most ezt a 3 pontod!
Körzővel megszerkesztve, már eléggé pontos középpontot is fogsz kapni.
-
 #3251
#3251
magyarul a háromszög köré írható kör középpontját keressük.
innen meg Google vagy Wiki
Ímhol e -
 #3250
#3250
köszi szépen majd ha felkelek megpróbálom :) -
 #3249
#3249
AB és BC szakaszra felírod az oldalfelezőt/szakaszfelezőt.
AB-re:
Először a két ponton átmenő képlettel felírod az AB szakasz képletét(vagyis az A és B ponton átmenő egyenes egyenletét). Ebből kinézed a normálvektort.
Utána az AB szakasz felezőpontját[ (5;6) ha jól sejtem, és a normálvektort irányvektorként használva felírod a szakaszfelező egyenes egyenletét.
Ugyan ezt megcsinálod egy BC-re(de akár AC-re is), majd a két egyenes egyenletéből megnézed hol metszik egymást(egyenletrendszer).
Így leírva sokkal bonyolultabbnak tűnik, mint amilyen valójában;) -
 #3248
#3248
és azt hogy? AB BC CA szakaszt is megfelezem vagy hogy? akkor se 2 kordináta lesz hanem 6... :S -
 #3247
#3247
Szakaszfelező merőleges lesz a megoldás szerintem. -
 #3246
#3246
Kordináta geometriával kapcsolatban lenne 1 kérdésem :)
így szól a feladat:
Adjon meg egy olyan pontot ami egyenlő távolságra van az A(8;5), B(2;7), C(10;9) pontoktól.
Gondolkoztam hogy a súlyvonalakra vonatkozó tétellel kell-e ezt megoldani, de az nincs egyenlő távolságra a pontoktól tehát nem vágom :D -
polarka #3245 :) wolframot is csekkolod?
Én nem nagyon nézegettem Numberst, de most felkeltetted az érdeklődésem, ha lesz időm, majd nézem/olvasgatom. -
 #3244
#3244
:) már többször is olvasgattam Google books-on és erősen gondolkodom, h megrendelem... Néztem már. Mivel nagy (Numb3rs) fan vagyok (még ha mellé is van fordítva és a 2., 3. évad egy fos és amúgy is rózsaszín ködben úszik benne mindenki, az emberi kapcsolatok és a szereplők jellemei meg olyan gyermetegen vannak ábrázolva, stb, stb... Magyarul egy hányadék...), tehát ezektől eltekintve elég sok olyan dologra mutat rá, aminek ha utána bogarászok, akkor rengeteg viszonylag friss dolgot találok, amit nálunk nem is oktatnak.
A könyv azért izgat, mert az egyik szerző a matematikai tanácsadó a Numb3rs mellé (ha jól emlékszem) tehát van mögötte tartalom is. -
polarka #3243 1ébként érdekel a "The number behind 'Numbers'" angol könyv? cirka 200oldal és - az első fejezet alapján - inkább átlagembereknek íródott. -
polarka #3242 Most vettem a fáradságot, h olvasgassak róla és jólesett, egész 1szerű képlet, furcsa, h ilyen későn kezdték alkalmazni/találták ki.
abból, amit olvastam:
- több hasonló módszeren alapuló egyenlet van
- készítettek olyan progikat, amik a nyomozóknak elkészítik az adott szituációra a térképet
- gyakorlatilag, ha helyesen készült statisztikák és bűnözői profil alapján készül, akkor bármilyen sorozatos bűntett lehetséges forrása megtalálható
vagyis vmi nyomozónál érdemes kérdezni
Egyébként nyomozás során gondolom az adott úthálózatot, forgalmat is figyelembe veszik. Mivel ugye ez a Manhattan-távolság mérés a rácsvonalas településekre ideális. Sőt még bonyolítja a helyzetet, ha az elkövető tömegközlekedéssel is utazhat. Tehát ha finomítunk, akkor alkalmazni kéne minden tetthelyhez egy finomító súlyozó térképet.
ne az elkövető lakhelye jöjjön ki:
1. - kijelölsz 1 környéket, amihez semmi nem köt
- a környéken kívül koncentrikusan helyezed el a tetthelyeket
2. - a valós puffer zónádban is helyezel el
3. - ha egyenes mentén helyezzük el, akkor ha jól vizualizálom, akkor a két oldalán kapunk lehetséges területet, ezt is csak tologatni kell
általánosan: mivel a formula/módszer a statisztikákon alapul, úgy cselekedni, ahogy a meggondolatlan, többségben levő elkövető nem tenne
- illetve, aki mindig utazik, így állandó lakhelye nincsen arra sem fog működni
az üzletek elhelyezése sztem jó alternatív felhasználás
- esetek helyére pl. tömegközlekedés megállóhelyei jöhetnének, puffer zóna nélkül, utasszámátlaggal súlyozva
- illetve még lehetne hasonló profilú üzleteket negatív valószínűséggel felvenni, vásárlói véleményezés alapján ezt a konkurenciát súlyozni, puffer zóna nélkül -
 #3241
#3241
Még nem bogarásztam utána, de nem tudnék kapásból olyan embert mondani, aki sorozatgyilkosok lakhelyét/tartózkodási helyét efféle valószínűség számítási módszerekkel keresgélné. Persze nem is biztos, h olyan sok efféle eset van.
A másik persze rögtön adott: hogyan kell az áldozatokat elhelyezni, hogy ne az én lakhelyem legyen a maximális valószínűség zónájában?
És persze az is eszembe jutott, h mi másra is lehet ezt még használni? Pl. Hová helyezzünk üzleteket, hogy maximális legyen azoknak a forgalma (a legtöbben menjenek oda - ott legyen a látogatási maximum). -
polarka #3240 Értem. De elvileg, ha értenek hozzá, akkor valszeg az angol megnevezést is ismerik. Pláne, ha még körül is írod. Meg ha már ilyen hozzáértő embereket ismersz, akkor meg is kérdezheted őket.
Nah mind1, gondolom ez nem ilyen 1szerű
-
lotsopa #3239 De, kérdezni lehet, csak nem azt a választ fogod kapni amit szeretnél. -
 #3238
#3238
Az, hogy jó lenne tudni, ha erről akarok beszélni magyar nyelven, akkor egy dologról beszéljek azokkal, akik talán értenének hozzá... Pontosan ez a probléma: addig nem lehet kérdezni, míg nem tudod, hogy mit akarsz kérdezni! -
polarka #3237 sztem nem valszínű, h találnál bármit is, ha tudnád hogyan használják legalábbis a neten
az angollal mi a baj? -
 #3236
#3236
Volt egy kérdésem ITT, valaki tud erről vmit??? -
lotsopa #3235 Eltűnt a formázásom. :( A sok space-em. :) -
lotsopa #3234 Hali. Csaba+Dani>Bea+Emma+Anna
X eleme N. 4x+x+40>2x+x-20+x
Bea: 2x 40 könyv 5x+40>4x-20 /-4x
Csaba: 4x 80 könyv x+40>-20 /-40
Dani: x+40 60 könyv x>-60
Emma: x-20 0 könyv ( x>19 )
Anna: x 20 könyv
-
BaltásRém #3233 Sziasztok !
ááá de jó, hogy megtaláltam ezt a fórumot, pont ilyet kerestem.
Szöveges feladat, 6.osztályos feladvány ! :)
Ám megválaszoltam a feladványt, mégis kíváncsi lennék arra, hogy tud-e valaki mégkielégítőbb választ rá !
Íme a feladat:
"Beának kétszer annyi, Csabának négyszer annyi, Daninak 40-el több, ,Emmának 20-szal kevesebb könyve van, mint Annának.A két fiúnak együttvéve több könyve van, mint a három lánynak.
Hány könyvük lehet az egyes gyerekeknek ?"
-
pet0330 #3232 Sziasztok!
Valamikor elkezdtem képleteket kitalálni az első n darab k-adik hatványszám összegére, és ha jól emlékszem k=2 és k=4 vagy 8 (nem emlékszem) az jött ki hogy az utóbbi kifejezés pont a négyzete az előbbinek. Ez igaz tovább is valahogy? -
 #3231
#3231
ha van vki itt aki ász diff. egyenletrendszerekből az segíthetne:
van egy diff. egyenletrendszer ami így néz ki:
ahol C ismert mátrix. Ennek az egyenletrendszernek a megoldása állítólag
ahol c[alsóindex(s)] a C mátrix sajátértékei. G-k pedig konstansok. A kérdésem az h ez így jól van e, és ha igen, akkor mi szerint rendeljük hozzá a sajátértékekhez az indexeket. Tehát az f[alsóindex(1)] függvényhez melyik sajátérték fog tartozni?
(remélem érthető a dolog =D) -
polarka #3230 "Azt már sokat kijelentették hogy a tudomány nyelve a matematika"
Pontosan, és még fizikai ismeretek nélkül is teljes mértékben megáll a saját lábán. 1ébként én is szeretem a fizikát. -
polarka #3229 xD ott a pont -
 #3228
#3228
Ha korrektül kellene megfogalmazni, akkor azt lehetne mondani pl, hogy "a természettudományok anyaggal és energiával foglalkoznak", és akkor már egészen közel vagyunk a valósághoz, csak azt nem tudom, hogy ezzel akkor most mennyivel lettünk előrébb? Merthogy ez már úgy 200-250 éve így van... -
uwu #3227 OMG
Komolyan mondod, hogy meg se fordult a fejedben, hogy ez egy kritikus irónia volt?
Csak mert a hablaty amit összehordtál, kb ugyanennyire megalapozott. -
lotsopa #3226 Nem mindent betűkkel és számokkal írunk le, de eddig ez nem nagy tévedés. Maga a megállapítás hogy a kommunikáció az alapja mindennek elég közel áll a valósághoz. Az információ közlése, cseréje a világ alapja. A kommunikáció szakos végzettségűek nem sokat tudnak a 'való világról'. :) Ők nem állnak egy tudós felett sem szerintem.
De én nem is akarom sorrendbe állítani ezeket a tudományokat. Kétségtelen hogy mindegyik fontos és szükséges, vitatkozni rajta hogy melyik a felsőbbrendű szerintem értelmetlen, kapcsolatban állnak egymással, egymásra épül némelyik.
Azt már sokat kijelentették hogy a tudomány nyelve a matematika, ezzel lehet leírni s valamennyire megérteni is, de mégis csak a fizika kelti 'életre' a matek nyelven megfogalmazottakat. Ez a kettő nem szedhető szét, de nem egy és ugyan az! Éljenek a tudományok. :-) -
uwu #3225 Hülyeség, minden tudomány jelekkel foglalkozik, mert mindent betűkkel és számokkal írunk le, így aztán mindennek az alapja a kommunikáció. Tehát a kommunikációszakos végzettségűek minden tudós felett állnak. -
lotsopa #3224 Neten valahol olvastam egy olyan érvet hogy természettudományok: fizika, kémia, biológia, földrajztudomány, matematika, geológia, meteorológia, csillagászat, orvostudomány, mezőgazdaság-tudomány, genetika ezek mind "atomokkal" foglalkoznak, és az atomokkal kapcsolatban a fizika az úr. Persze ez az érv humorosan értendő, mégis van benne valami... -
polarka #3223 Márpedig a matek a legalapabb. A matekosok foglalkoznak olyan kérdésekkel is aminek a valósághoz nem kell/nincs is semmilyen köze. Végig gondolják azon eseteket is amiket, a fizikusok alapból kihúznak, mert tudják, h az nem történik meg.
Sőt a mostani néhány évtizedig mindig előrébb járt a matek, mint a fizika, csak most várnak vmi új fejleményre a matek terén a fizikusok. (Legalábbis Michio Kaku ezt állította, meg talán Stephen Hawking is) -
lotsopa #3222 Amúgy az érettségi is jó bizonyos esetekben. :)
Egyébként ha már valamilyen dolog 'összefogja'- ahol mind a négy tárból szerzett tudás jól jön- az talán a nanotechnológia. -
lotsopa #3221 Szerintem a fizika az alapja a többinek, márha te a matekot raktad oda.
Úgy írtad hogy a matek fogja össze, a fizika írja le a 'világunkat' tudtommal, még ha nem is hibátlanul. :)
A fizika szerintem a legcsodálatosabb tantárgy, és ami nagyon sajnálok hogy vajmi kevés tudással rendelkezem róla, de igyekszem a tudást magamba szippantani. :) -
polarka #3220 konkrétabban (ill. wtf)?
- mind természettudomány
- fizika, kémia, biosz a tapasztalatokból és a matekból épül fel(≡ matek fogja össze), ami pedig axiómákból és azokból levezetett tételekből -
 #3219
#3219
érettségi? -
lotsopa #3218 Mi fogja össze a matematikát, fizikát, kémiát, biológiát? -
polarka #3217 324 a jó megoldás.
A 4*3*4*3*4-ben olyan lehetőséget is számolsz, ahol a 3. ajtó azonos színű a 2-kal.
Ha nem hiszed, rajzold fel gráfszerűen, ahogyan általánosban is magyarázni szokták. -
lotsopa #3216 Sajnos igen, mert ha az első és a harmadik egy színű akkor a második a maradék három szín közül kerülhet ki, viszont ha az első és a harmadik eltérő színű akkor már csak két szín közül választhatunk.
Ha n darab szín közül választhatunk akkor az első esetben a lehetőségek száma n-1, a másodiknál n-2 lesz. Lényegében csak le kell vonni a szomszédos részeket, attól függően hogy azonos színű a két nem szomszédos szoba.