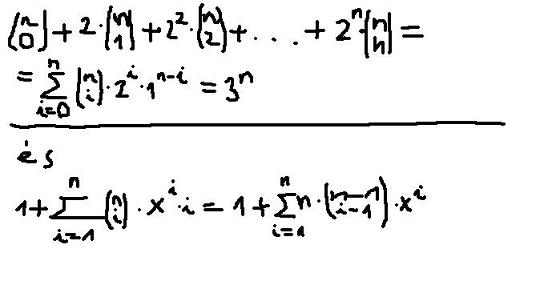4415
Matematika feladatok
-
#3415
Nagyon köszönjük:)))
#3409 : kiderült, hogy megvan neki:)))) -
lally #3414 Gratulálok a FizKém ZH-hoz !!!- má_csak azér' is, mer':
kedvenc "számtan tanárom"; prof.H.M. szavait idézve
(akkor, amikor a krétás kezével, még a bajuszát is tekergette):
"...tudjuk, hogy csalnak (! ), és; Mégsem sikerül ŐKET, tetten is érni !" -
Pio #3413 Jaaaa tényleg. :D
Szabó Misi 4ever! :D -
 #3412
#3412
biomérnök, de már beszéltük szmötyi kapcsán :D -
Pio #3411 Fizkém? Vegyészkedsz valamerre? :) -
 #3410
#3410
/off:
10 pont lett a 15ből a fizkém .......
(: -
lally #3409 Javasolnám; Szólj a barátnődnek, hogy egy könyvtárból majd kölcsönözze is ki:
"Bárczy Barnabás:Differenciálszámítás"-át !!!
-s, még az sem zárható ki, hogy: abban a ZH-ban, meg is kérdezik majd, az
"e"-fogalmát! -
 #3408
#3408
jah (:
amúgy ezeket már egy jobb PDA progi is tudja, pl. SpaceTime Mathematica
jól jön ZH-kon :D -
Koppixer #3407 Egész jó ez a WolframAlpha! Hasznát fogom venni.
Ráadásul jópofa:
oldal alján: "Computation timed out. Experimental feature: Try again with more time" :) -
 #3406
#3406
???? még nem megy a linkelés? 
http://www.wolframalpha.com/input/?i=e^%28-x^2%2F2%29 -
 #3405
#3405
[URL=http://www.wolframalpha.com/input/?i=e^%28-x^2%2F2%29]link[/URL]t lehagyta -
 #3404
#3404
[URL=http://www.wolframalpha.com/input/?i=e^%28-x^2%2F2%29]e^(-x^2)[/URL] -
#3403
Sziasztok,
Az e a (mínusz x négyzet per kettediken) függvényt tudnátok elemezni?
(paritás, folytonosság, határértékek, monotonitás és szélsőértékek, konvexitás-konkávitás, inflexiós pont) részmegoldásoknak is örülnék..
a barátnőmnek kell:)
tehát a függvény:
-
gregtom6 #3402 Új kérdés:
Honnan tudnám kitalálni behelyettesítgetés nélkül, hogy a szumma i=0-tól n-1-ig : n-i az egyenlő szumma j=1-től n-ig: j -vel?
Valamint, ha nem úgy indexelem a szummát, ahogy a füzetben van, akkor rendszerint elakadok, mert pl ebből: szumma i=1-től n-ig : n-i+1 hogy jöhet ki a fenti szummák valamelyike?
Márpedig ha máshogy kezdem el indexelni a szummát, akkor ez jön ki.
Pedig elvileg ez az indexelés is ugyanazt a sorozatot adja meg. -
gregtom6 #3401 Megvilágosodtam:D
Kösz. Hát így oké, hogy látom a két oldalt, és tudom, h egyikből hogy jön a másik, de magamtól nem írtam volna soha így át a bal oldalt a jobb oldal értékének. -
Pio #3400 Eddigiek alapján ez simán kitalálható, szerintem próbálkozz vele, így tudod tesztelni, hogy tényleg érted-e a témát.
Ha végképp nem megy:
2^(n+1)-et felfogod (1+1)^(n+1)ként, amire felírod a binomiális tételt.
Mivel 1-nek minden hatványa 1, ezért a szorzatoknál a hatványok nem számítanak semmit, gyakorlatilag ezt kapod:
(n+1 alatt 0) + (n+1 alatt 1) + .... (n+1 alatt n+1)
A bal oldal pedig:
............... (n+1 alatt 1) + .... (n+1 alatt n+1)
Tehát ugyan az, csak a jobb oldalon marad egy (n+1 alatt 0), de az pont 1 és azt le is vonjuk, tehát egyenlőek. -
gregtom6 #3399 Oké, kösz, és szumma i=0-tól n-ig (n+1 alatt i+1) -ből hogy lesz 2 az n+1-edik hatványon -1?? -
Pio #3398 Kicsit a másodikat helyesbítem, mert xˆi-t nem emelünk ki, nem lehet, de beláttuk, hogy minden a feladatnak megfelelő n-re, i-re:
(n alatt i) × i
EGYENLŐ
(n-1 alatt i-1) × n
Akkor nyilván minden a feladatnak megfelelő n-re, i-re, x-re:
(n alatt i) × i × xˆi
EGYENLŐ
(n-1 alatt i-1) × n × xˆi
És készen vagyunk. -
Pio #3397 Boccs, teljesen elfelejtettem, hogy betetted a képet, remélem még nem késő.
Első:
Mind a 3 képlet a (2+1)^n felírása a binomiális tétel alapján.
Az első a felsorolós alak, a második a summa-s alak, a harmadik pedig szimplán összeadja a 2+1-et.
-------------
Második:
Az egyenlet mindkét oldalán van 1+, tehát elhagyható.
A summáknak ugyan annyi tagja van és minden tag szorozva van x^i-vel, tehát az kiemelhető, oszthatunk vele (x nem= 0 kikötés mellett) elhagyható.
Gyorsan nézzük, ha x=0, akkor mi a helyzet. A summa összes tagja 0 lesz, tehát 1=1, ami jó.
Tehát annyi maradt a kérdés, hogy a summában maradtakkal mi a helyzet:
(n alatt i) × i
EGYENLŐ-E
(n-1 alatt i-1)×n
Ez viszont elég egyszerűen belátható faktoriális alakból.
Első:
Számláló: n! × i
Nevező: i!×(n-i)!
i-vel egyszerűsítek:
Számláló: n!
Nevező: (i-1)!×(n-i)!
Második:
Számláló: (n-1)! × n
Nevező: (i-1)!×(n-1-(i-i))!
Számlálót egyszerűbb alakra hozom, nevező második tagját kiszámolom:
Számláló: n!
Nevező: (i-1)!×(n-i)!
Tehát egyenlőek. -
forrai #3396 Szia nonicks
A fizikában válaszoltam egy kérdésedre. -
Pio #3395 Ilyenre szerintem nem fogsz találni képletet, hisz oszthatósági szabályok alapján kizárás után is marad 4 számjegy, amikre vizsgálni kell, szóval akár 100 közeli prímek is feltűnhetnek a felbontásban, addig pedig ember legyen a talpán, aki formularizálja az összes oszthatósági szabályt.
Annyira viszont nem nehéz végiggondolni.
Azonnal kizárhatóak:
- a párosok, hisz azok a végére írva 2-vel oszthatóvá teszik a számot
- az 5, hisz az a végére írva 5-tel oszthatóvá teszi a számot
Maradt: 1, 3, 7, 9, de ez egyből ki is esik, ha végigfutsz rajta a 7-tel oszthatósággal, mert 137-2×9=119, 11-2×9=-7, ami osztható 7-tel.
A maradékból csökkentő sorrendben a lehetséges 3-asok prímségének kitalálása az egyetlen kihívás igazából, erre némi tipp:
3-mal való oszthatóságot triviális vizsgálni, 2, 5 más kiestek, 7-tel való oszthatóság maradt 1jegyű, de az szintén pillanatok alatt ellenőrizhető a megfelelő oszthatósági szabállyal, ezért tegyük ezt első körben, ha valamire nem nyert, akkor azt hagyjuk a végére, mert az melósabb. Ha esetleg tudod a 11, 13, 17, 19, 23 oszthatósági szabályait, akkor nem is kell végére hagyással bajlódni, egyből kiszámolhatsz mindent.
973 - 97-6=91, 9-2=7, osztható 7-tel
971 - nem osztható 7-tel, potenciális megoldás, nézzük meg 7-tel más sorrendben a jegyeit...
917 - 91-14=77 osztható 7-tel, nem nyert
931 - 93-2=91, 9-2=7, osztható 7-tel
731 - nem osztható 7-tel, potenciális megoldás, nézzük meg 7-tel más sorrendben a jegyeit...
713 - ez se
371 - 37-2=35, ez már igen
Tehát 3jegyű megoldás sincs, innen pedig végképp könnyű a dolgunk és úgy néz ki, hogy meg is találtad a helyes eredményt.
Talán arra, hogy a 3jegyűek közül mindegyik osztható 7-tel valamelyik permutációban lehetett volna valami általános igazolást találni, de felesleges volt, fejben, esetszétválasztással megoldható volt a feladat nagyjából 3 perc alatt.
Számelméletből, főleg középiskolában nem minden formulásítható, sokszor kell gondolkodni, ügyeskedni, az ismert fogalmakat, szabályokat okosan alkalmazni, hogy gyorsan, hatékonyan meglegyen a megoldás.
Ja és bár valamiért nem szokás tanítani, érdemes ismerni a prímek oszthatósági szabályait 23-ig, nagyon könnyűek és sok időt lehet velük spórolni. -
 #3394
#3394
Melyik az a legnagyobb, csupa különböző számjegyet tartalmazó pozitív egész szám, amelynek a számjegyeit
tetszőleges sorrendben véve mindig prímszámot kapunk?
ezt hogyan lehetne képlettel felírni?
(amúgy 97 a megoldás?) -
 #3393
#3393
igen, és ezért akartam megnézni, hogy jó-e, mert elvileg azt is ki kénne neki írnia -
 #3392
#3392
az én számításaim szerint a megoldások +4 és -4 lennének, de akkor a nevező zérus, így ezek nem megoldások. -
 #3391
#3391
mert nincs megoldása az egyenletnek? -
 #3390
#3390
wolframalpha-ára beírtam hogy (x+4)/(x-4)+(x-4)/(x+4)=64/((x-4)(x+4)) gondoltam leellenőrzőm, hogy x1=0 x2=48 lesz-e és nem ad ki eredményt? ez mitől lehet? 

-
gregtom6 #3389 Na itt a felső rész volt az, amit korábban leírtam.
Az alsó rész pedig egy új dolog, mintha valami szabályt alkalmazva jönne létre a jobb oldal.
Kérdezem én, hol vannak ezek a szabályok leírva? -
gregtom6 #3388 -
Pio #3387 "...2 az iediken*1..."
Meglepne... -
 #3386
#3386
lehet h binomiálisra gondol? 
-
Pio #3385 Szerintem ezt is rosszul írtad le, mi értelme van szorozni 1-gyel bármit is? Nem hinném, hogy egy feladat képletében 1-gyel szorozgatnának...
Inkább rajzold le paintben amúgy, ha zavar az, hogy textként kell leírni és emiatt rosszul írod le. -
gregtom6 #3384 Viszont van egy másik dolog, amit nem értek.
(n 0)+2*(n 1)+2négyzeten*(n 2)+...+2 az n-ediken*(n n)=szumma i=0-tól n-ig (n i)*2 az iediken*1 az n-i-ediken=3 az n-ediken.
Ezt a szumma átalakítást nem értem, mert eddig ilyen átalakításnál nem vettük úgy, hogy hatványoztuk a binom. tételben a 2 binomot(azt hiszem, ez a neve).
Így felvetődik a kérdés, hogy hova tűnt az (n i) a 3 az n-ediken mellől?
Vagy itt gyakorlatilag tényleg csak a binomiális tétel lett alkalmazva? -
gregtom6 #3383 De közben rájöttem, szerintem el volt írva, és akkor
Szumma i=0-tól n-ig (n i)négyzeten=szumma i=0-tól n-ig (n n-i)*(n i) akart ez lenni, és ennél a megközelítésben ugye (n n-i)=(n i)-vel, a Pascal-háromszög miatt, tehát valójában tényleg (n i)*(n i) volt a fenti egyenlet jobb oldalán.
És így akkor már érthető. -
Pio #3382 Valamit elírtál az első summa-ban nem is szerepel i. -
gregtom6 #3381 Hy all!
Szumma i=0-tól n-ig (n 1)négyzeten=szumma i=0-tól n-ig (n n-1)*(n i) ???
Ha igen, miért? És hol találhatnék ilyen szummás, binomiális együtthatós azonosságokat?
a (valami valami) az binomiális együttható lenne(kombináció). -
 #3380
#3380
Köszi szépen. -
Pio #3379 Nekem ezen simán bejön a 18. oldal...
-
 #3378
#3378
Úgy tűnik az oldalszámok nem egyeznek. Nekem az az oldal kéne, ami itt a 18. oldal:
http://books.google.hu/books?id=ARUdRGEosF0C&printsec=frontcover&dq=bevezet%C3%A9s+az+algebr%C3%A1ba&source=bl&ots=eW6qjfNjGZ&sig=1uv5s6cnhARMOof6T_VI4fx6wZ0&hl=hu&ei=DbbCTKWfBYiVswagwYi5CA&sa=X&oi=book_result&ct=result&resnum=6&ved=0CC8Q6AEwBQ#v=onepage&q&f=false -
Pio #3377 -
 #3376
#3376
Valaki be tudná nekem szkennelni a "Bevezetés az algebrába" című tankönyv 18. oldalát? Azért csakis azon oldal kell, mert a neten olvasom a könyvet, és pont az hiányzik.
Köszi.