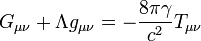1406
Tényleg nem létezik?
-
Albertus #765 "Nem, maga a hatás nem lép fel a kisautónál."
Éppen ellenkezően! A Coriolis erő, mint ahogyan nevében benne van:ERŐ,
csak ott jelenik meg amikor erőhatás ébred a forgó és az egyenesvonalú mozgások KONTAKT találkozásakor.
A csak relatív mozgáskor NEM LÉP FEL A Coriolis erő.
"Inerciarendszerből szemlélve a dolgot"
Gravitációs mezőben erőhatás alatt felejtsük el az inerciális mozgást.
Még az inga esetében is egyenletesen gyorsuló a mozgás, ezzel a vízszintes irányú sebességvektor szintén egyenletesen változó nagyságú.
Azaz az elfordulás szemléltetésére jó az inga, de a számításokhoz már azért nem jó, mert egyszerre háromféle gyorsulás hatásának az eredményét mutatja.
Egy távoli puskagolyóhoz lehet inercia rendszert rögzíteni, és ha ezen golyó "alatt" tömegtelen korong forog, akkor a korong pontjainak mozgását szemlélhetjük inercia rendszerből, azaz a golyó rendszeréből.
de miután ezen esetben nincs erőhatás, azaz a Coriolis erő sem jelenik meg,
ezért értelmetlen olyan példán tárgyalni a Coriolis erőt ahol nem jelenhet meg.
"Viszont többször nem szeretném leírni ugyanezt..."
Ennek nagyon örülök! Annyi butaságot, amit eddig leírtál, én sem szívesen olvasnék el újra.
Amíg nem érted meg a Coriolis erő működését, addig azt sem értheted meg, hogy az a Coriolis erő ami a körvezető felett haladó elektronra hat, hogyan jön létre.
Ezzel ugyanúgy mint Lorentz és Einstein, te sem fogod megérteni, hogy a Maxwell-Hertz elvek és a látszólagos töltéseltolódás helyett az elektron spinje okozza az elektronra ható Coriolis erőhatást.
-
 #764
#764
http://hu.wikipedia.org/wiki/H%C3%BArelm%C3%A9let -
 #763
#763
Na itt jön be az, hogy a fény (illetve pontosabban az elektromágneses sugárzás) kettős természetű, és attól függ, hogyan viselkedik, hogy melyik tulajdonságát nézed.
A fényelnyeléskor és fényvisszaverődéskor a fény hullámként viselkedik, nem részecskeként. -
 #762
#762
Lehet vhol olvasni ezekről az elméletekről a NET-en magyarul vagy németül? -
Albertus #761 "LOL fizikus vagy?
És nem megy a matek?
Egy mezei mérnök jobban vágja a matekot mint te?"
Nos, nem vagyok fizikus. Azt írtam, hogy "A fizikus kollégák!"
Bár igaz, sokféle képzettségem van, de köztük fizikus nem vagyok.
És miért ne menne a matek?
Talán abból gondolod, hogy érthetően magyarázok? Feleslegesen nem dobálózom függvényekkel?
Meggyőződésem, hogy ha így sem tudod követni a soraim értelmét, akkor diff.egyenletekkel még kevésbé tudnád.
-
 #760
#760
"A kisautós modell is jó, a puskagolyós is, csak mindkettőt helyesen kell értelmezni."
Nem, maga a hatás nem lép fel a kisautónál.
Az inga valóban jó példa, és ott sincs kapcsolat(erőhatás nem lép fel) az inga, és az alatta elforduló Föld közt. Tehát az inga is szép példa arra, hogy a kiskocsis modelled miért nem jó.
"Ugyanis, ha a forgó felszín nincs kapcsolatban az egyenes vonalú mozgást végző testtel, akkor tisztán erőhatás mentes, relatív elmozdulás van, és NINCS azaz nem ébred Coriolis erő."
Inerciarendszerből szemlélve a dolgot. Igen, a Coriolis-erő a relatív elmozdulást magyarázó fiktív erő, ami inerciarendszerből nézve nem létezik. Hajrá, közeledsz hozzá, hogy megértsd!
Ha azonban a megfigyelő is a puskával együtt forog, akkor ahhoz, hogy a golyó pályáját leírjuk _fel_kell_vennünk_egy_fiktív_erőt_, hogy Newton első törvénye ne sérüljön. Mert a megfigyelt mozgás nem egyenes vonalú. Tehát erőnek kell lennie. És mindez csak azért _látszik_ így, mert a megfigyelő gyorsuló vonatkoztatási rendszerben van.
"Amikor viszont kapcsolatban áll a két mozgást végző akkor ébred a kisautónál leírt érintő irányú Coriolis erő."
Nem az nem Coriolis erő, hanem simán súrlódás útján átadott, sima, hétköznapi erőhatás, ami a kisautót körmozgásra kényszeríti. Mivel adsz neki egy v=konstans sugárirányú kezdősebességet, ezért nem körpályát ír le (inerciarendszerből szemlélve), hanem arkhimédeszi spirált.
"Valamint akkor tartható meg az egyenes vonalú mozgás, ha a Coriolis erővel egyenlő nagyságú, de (a forgással) ellentétes irányú (érintő irányú) ellenerővel hatunk a testre."
Amit Coriolis erőnek nevezel, az a súrlódás. El is koptatná a kisautód kerekeit, ha megakadályozod, hogy a koronggal együtt forogjon.
"Azaz tévesen állítottad, hogy a Coriolis erő nem létező."
Még mindig hibás a kiindulásod, így a következtetéseid is.
"Mert csak akkor nem létező, amikor csak relatív elmozdulás van, erőhatás nélkül, mert ekkor valóban nincs Coriolis erő."
Erről beszélek, hogy a Coriolis erő megjelenése vagy nem megjelenése a megfigyelő helyzetétől függ, hogy inerciarendszerből szemléli a dolgot, vagy a rendszerrel együtt forog. A Coriolis-hatás bizony kizárólag a forgó felszín és a nem a felszínnel együtt forgó test relatív elmozdulása.
"Vagyis olyan esettel próbáltad igazolni a Coriolis erő nemlétezését amikor egyébként sem jelenik meg."
1. esetben megjelenik, pedig ott sincs kapcsolat a Föld és a golyó közt, mégis úgy látjuk, hogy kanyarodik.
Viszont többször nem szeretném leírni ugyanezt... -
Albertus #759 "De az anyagban is kell hogy legyenek fotonok"
Sőt mi több! Az anyag az állóhullámszerű pályán haladó fotonok tömegéből épül fel a legújabb elméletek szerint.
Ezért tapasztaljuk azt, hogy ha az anyagot gyorsulásnak tesszük ki akkor fotonok szakadnak le róla és "világítani kezd"..
Jó példa erre az elektron, amikor gyorsulás hat rá, akár egy mikrofonban létrejövő feszültség változás hatására, akár egy izzószálban, vagy a LED-ekben, minden gyorsulásra e.m. hullámok, azaz fotonok kisugárzásával reagál.
-
Albertus #758 Egyébként a "foton sem működik így"!
Csak Einstein elmélete alapján születtek ilyen feltételezések. Amihez hozzá kell tenni, hogy Einstein sem állított ilyen következményt.
Ugyanis az Einstein által átvett Lorentz függvényeknek v=c helyen szakadása van.
Nem véletlenül vezettem le a sebességvektorok derékszögű háromszögéből a v vektorra merőleges irányú d sebességvektort, és a ßéta
ß=c/d arányát ebből képeztem (Gézoo kolléga ötletét átvéve,)
Ugyanis ekkor t'=t/ß=t*d/c ahol a ßéta értéke, lévén hogy v=c
azaz d=gyök(c²-c²)=0 1/ß=d/c=0/c=0 így:
t'=t*0/c=0
Ez az az összefüggés aminek alapján "továbbgondolva" Lorentz ill. Einstein okoskodását, a foton ideje t'=0 értékű.
Ha csak az Einstein által használt ß=1/gyök(1-(v/c)²) összefüggést használnánk, akkor miután a v=c esetében v/c=1 és (1-1²)=0 .. ill. gyök(0)=0 értékű, így a ß =1/0 értelmezhetetlen lenne.
A függvénynek ez az alakja azt a látszatot kelti, hogy a foton ideje bármilyen lehet, nem tudhatjuk, mert az a függvény amit a kiszámításához használunk v=c esetére nem használható.
Ezzel szemben a másik alakkal látható, hogy nincs a függvénynek szakadási helye v=c esetében, hanem azt az eredményt adja, hogy látszólag áll a foton ideje.
Ezen a ponton nem szabad elfeledkeznünk arról, hogy az egész relativitás a látszatokról szól!
Azaz arról, hogy látunk valamit és a látványból kiszámoljuk, hogy a látott-megmért értékek a valóságban milyen értékeket jelentenek.
Vagyis amikor a látvány azt mutatná, hogy t'=0 akkor
a foton ideje a valóságban t#0
Magyarul a foton "rendszerében" sem lassul le az idő és ott sem áll meg.
Csupán az lenne a látszata, miután a foton "rendszeréből" az ottani eseményekről tudósító fény csak c sebességgel távolodhat az eseménytől, azaz hozzánk c-v=0 sebességgel közeledve, sohasem érkezhet meg.
-
 #757
#757
De az anyagban is kell hogy legyenek fotonok. Hogy is tanultuk a fényelnyelést, fényvisszaverést? Ugye a foton nem fékez le és végez elkerülő manővert egy "anyag"-gal találkozva?:D -
Albertus #756 A kisautós modell is jó, a puskagolyós is, csak mindkettőt helyesen kell értelmezni.
Jó példa még erre: http://hu.wikipedia.org/wiki/Foucault-inga
Ugyanis, ha a forgó felszín nincs kapcsolatban az egyenes vonalú mozgást végző testtel, akkor tisztán erőhatás mentes, relatív elmozdulás van, és NINCS azaz nem ébred Coriolis erő.
Amikor viszont kapcsolatban áll a két mozgást végző akkor ébred a kisautónál leírt érintő irányú Coriolis erő.
Valamint akkor tartható meg az egyenes vonalú mozgás, ha a Coriolis erővel egyenlő nagyságú, de (a forgással) ellentétes irányú (érintő irányú) ellenerővel hatunk a testre.
Azaz tévesen állítottad, hogy a Coriolis erő nem létező.
Mert csak akkor nem létező, amikor csak relatív elmozdulás van, erőhatás nélkül, mert ekkor valóban nincs Coriolis erő.
Vagyis olyan esettel próbáltad igazolni a Coriolis erő nemlétezését amikor egyébként sem jelenik meg.
-
 #755
#755
Egész egyszerűen a foton így működik, az anyag meg úgy. Nem feszeget semmi semminek a határait. A foton fénysebességgel halad, az anyag erre nem képes. (A fénysebességhez közeledve a tömeg a végtelenbe tart, így a gyorsításhoz szükséges erő is a végtelenbe tart. A fénysebességet épp nem lehet elérni, mert ahhoz egy végtelen nagy tömeget kellene egy végtelen nagy erővel meglökni, viszont nem létezik olyan, hogy végtelen nagy erő.)
A klasszikus értelemben vett anyag protonokból, neutronokból és elektronokból áll, a foton meg foton. Tehát nem anyag.
Viszont mind elemi részecskék, a p+, n0 és e- anyagi elemi részecskék, a foton meg a fény elemi részecskéje. De a foton határozottan nem "semmi", csak nem anyag.
A foton kettéhasításáról én nem hallottam, így nincs hozzáfűznivalóm... Az anyag elemi részecskéit már sikerült szétbontani, nem elképzelhetetlen, hogy a fotont is szét lehet. -
 #754
#754
Szándékosan hoztam fel új modellt, mert a tiéd szart sem ér, már megbocsáss. Rossz modellből nyilvánvalóan rossz következtetésre jutsz. A kiskocsi semmilyen módon nem szemlélteti a Coriolis-hatást, a modell erre nem használható.
Az én modellemre figyelj, és az én magyarázatomra, ne kisautózz össze-vissza.
Eszközök:
Föld, puska, puskagolyó.
Vonatkoztatási rendszerek:
1. esetben a puskából nézzük, ekkor a golyó kanyarodni látszik, van Coriolis-erő
2. esetben az űrből nézzük, látjuk a Földet forogni, látjuk, hogy a puska is elfordul a Földdel együtt, és látjuk, hogy a golyó egyenes vonalú egyenletes mozgást végez, és nincs Coriolis-erő.
Esemény:
Puskából kilőjük a puskagolyót.
Magyarázat:
1. esetben a rendszerünk nem inerciarendszer, mert a rendszer gyorsul (centripetális gyorsulással, a körmozgás következtében, de ez most mindegy) A nem-inercia rendszerek jellemzője, hogy a mozgó rendszer gyorsulását az inerciarendszerben mozgó tárgyakra fiktív erőként kell alkalmazni. És a hangsúly a fiktív szón.
2. esetben a rendszerünk inerciarendszer, nem gyorsul, így nincs szükség a fiktív erőkre, minden mozgás függetlenül megfigyelhető, nincsenek a rendszer gyorsulásából származó hatások.
Dióhéjban: A kisautós modelled sajnos teljesen téves, a kerekek súrlódásának hatása és a kapcsolat a forgó rendszerrel teljesen kiküszöböli a Coriolis-hatást.
1. esetben a korongról nézve a kisautó e.v.e.m.-t végez, 2. esetben a mozgás arkhimédeszi spirál utat ír le.
"Lendítsd meg sugár irányban azt a kisautódat, amelyiket tologatni szoktad! Ha nem hatna rá a Coriolis erő akkor egyenesen halad a megindítás irányába..
Különben elfordul a forgás irányába."
Amit itt írtál, az bizony a kerekek súrlódásának a hatása.
Azt az egyet nem értem, hogy ha a kinematikával ilyen problémáid vannak, akkor mi a francot akarsz a relativitáselmélettel? -
 #753
#753
Kb. annyit jelent, hogy "az anyag" nem, de a foton képes "téridőutazni" ill. azon korlátok határait döngetni, amiket az anyag nem?
Kicsit leegyszerűsített megfogalmazással?:D
A foton nem anyag? Már csak azért kérdezem, hogy volt egy cikk, amiben azt ecsetelték, hogy megfeleztek egy foton...stb. Hogy tudták megfelezni a "semmit"? -
uwu #752 LOL fizikus vagy?
És nem megy a matek?
Egy mezei mérnök jobban vágja a matekot mint te?
Hol a hiba tanárúr?
Egyébként nem a tényekkel van a gond, hanem azzal, ahogy azt a saját szád íze szerint kommentálod, terelsz, és megpróbálod lealacsonyítani a kollégád munkáját, miközben ő egy elismert világhírű fizikus, te meg egy senki vagy.
Egyébként nem hiszem ám el, hogy fizikus vagy, csak viccből válaszoltam így. Nekem volt fizikus ismerősöm, és veszettül vágta a matekot, pedig csak hallgató volt még. -
Albertus #751 A fizikus kollégáink nem vakbuzgó Einstein hívők. Ilyen hisztit nem is rendeznek mint ti.
Főleg nem a történelmi tények felemlítése kapcsán.
"Elméleti fizikus volt ,a dolgát csinálta." - Dehogy volt elméleti fizikus.
Segédhivatalnok volt. Szabadalmi ügyintéző. Szép kék könyökvédőkkel.
Különben sem ő, hanem Lorentz és Lebegyev vezette le a "képleteket".
Einstein csak lemásolta tőlük..
-
Albertus #750 "Valójában nem kanyarodik, mivel nem hat rá erő, hanem a Föld fordul el alatta."
Szóval még azt sem értetted meg, hogy nem repül és nem puskagolyó..
Oké.. kisautót ismered?
Lendítsd meg sugár irányban azt a kisautódat, amelyiket tologatni szoktad! Ha nem hatna rá a Coriolis erő akkor egyenesen halad a megindítás irányába..
Különben elfordul a forgás irányába.
Na kipróbáltad?
"hogy ezek után hülyeségnek tűnik számodra a relativitáselmélet, "
Számomra nem tűnik hülyeségnek sem a specrel, sem az áltrel. Csupán mindkettő a látszatokról szól.
Az a hülyeség, amikor valaki azt hiszi a relativitásról, hogy a valóság modellje.
Nem. A relativitás csupán a látszatokat leíró modell.
Ami pedig Gézoo tanárurat illeti kétlem, hogy felfoghatnád a köztetek lévő hatalmas szintkülönbséget. Ezért nevét a szádra hiába ne vedd!
-
uwu #749 Van valami mondanivalód esetleg? Hol a hiba a képletben?
Csak fröcsögni fogsz amíg világ a világ? -
uwu #748 A vakbuzgó Einstein hívők alatt a fizikusokat kell érteni? 
Szerinted hogy kellett volna születnie a képletnek? Megvilágosodás hatására? Elméleti fizikus volt ,a dolgát csinálta. Tudod ők így dolgoznak már egy idaja, számolgatnak és képleteket írnak fel.
-
Albertus #747 Ezek szerint nem tudod, hogy ezt a függvényt hogyan kreálta Einstein..
Az a huszon..-sokadik változata.
Az elsőket a környezetében élők javították mert akkora hülyeséget adott.. Ebben a változatban már "csak" az együtthatók értékei változtak.
Egyébként még így is pontatlan. Csak a vakbuzgó Einstein hívők szent grálja.
-
uwu #746 Nagy szívességet tennél az emberiségnek, ha kijavítanád a következő képletet:
(wikiből vettem, jelöléseket ott megtalálod)
Nem vagyok jó másodfokú nemlineáris parciális differenciál egyenletek megoldásában, de ha villantanál egy részletes levezetést, rámutatva a hibára azt tudnám követni.
Amíg ezt nem teszed meg, nincs miről beszélni, ugyanis a gyakorlatban ezt használják, és működik. Sajnos gyűlöleted tárgya foglalta rendszerbe az akkori eredményeket, megteremtve a relativitás alapjait. Mindenki elismeri a munkáját kivéve az antiszemitákat, konteo-hívőket, és téged, meg pár nyomorultat. -
 #745
#745
Epic fail.
A kilőtt golyó egyenes vonalú egyenletes mozgást végez a valóságban is, csak egy mozgó megfigyelő számára kanyarodni _látszik_. Valójában nem kanyarodik, mivel nem hat rá erő, hanem a Föld fordul el alatta.
A fiktív, _nem_létező_ coriolis-erőt azért kell bevezetni, hogy a mozgó puska vonatkoztatási rendszerében ne sérüljön a erőegyensúly, mert ugye _látszólag_ van eltérés az e.v.e.m.-tól. Ha egy mindkettőtől független vonatkoztatási rendszerből nézed, akkor a golyó e.v.e.m.-t végez, a puska meg elfordul, és _nincs_ coriolis-erő. Q.e.D.
Csoda, hogy ezek után hülyeségnek tűnik számodra a relativitáselmélet, mikor azt hiszed, hogy érted, közben meg nem? Ha már coriolis-témában elkövetted ezt a hibát, nem lehetséges, hogy a relativitáselmélettel is ez a helyzet? Én a helyedben kicsit most csöndben maradnék, és átgondolnám, hogy mit nem értek... Egyébként ahogy én látom, ez a vonatkoztatási rendszerrel buzerálás nem megy neked, (áttérés egyikből a másikba, hogy a gyorsuló rendszereknek milyen következményei vannak, mi a valós, mi a látszólagos, stb.) közben a relativitáselméletnek meg pont ez a lényege.
Ja, és húzd ki a fejed Gézoo haverod seggéből, szerintem ő közben a markába röhög, hogy mekkora hülyét csinált belőled. -
Albertus #744 Nekem sem a paradigma sem Einstein fóbiám sincs.. Történelmi tényeket írtam le. Ti pedig a tényeket vitatjátok.
A relativitás alapja.
Lorentz megfigyelte, hogy a körvezető felett egyenes vonalon haladó elektronra kitérítő erő hat.
Pontosan úgy mintha az elektron áthaladna egy vele párhuzamosan mozgó töltéspár között és ezért F= k*Q²/R² erő hat rá. Azaz egy egyenes vonalban, sugár irányban mozgó vezetőben ez az F erő hat és elektromos feszültséget hoz létre a vezető végei között.
Különböző sebességekhez, különböző feszültség tartozott Lorentz mérései szerint.
Miután az elektron spinjét, töltésének előjelét, és a töltésének nagyságát 1905-ig senki sem ismerte, ezért Lorentz egy fénysebességgel terjedő sugárzásnak, amely Maxwell egyenleteiből következett, és a v sebességgel mozgó töltéshordozónak a kölcsönhatásaként feltételezte ez a polarizációs jelenséget.
És felismerte, hogy a polarizációs hatás a mozgások irányainak megfelelően, követi a Doppler hatásnál tapasztalt amplitúdó változást.
Amit úgy emlegettél, hogy a "derékszügű háromszög matematikája", az nem más, mint a lényeg, a mozgási sebességek arányainak meghatározásakor.
Ugyanis ha a sugárzás iránya a háromszög átfogója, akkor a vezető mozgásvektora (v) az egyik befogó, és az erőhatás azaz a potenciál kialakulásának az irányába mutató sebességvektor (d) közötti függvény alakja c²=v²+d² azaz a potenciál nagyságát meghatározó sebességvektor d=gyök(c²-v²) és ezen sebességvektornak és a fénysebességnek az aránya ß=c/d azaz ß=c/gyök(c²-v²)=
ß=1/gyök(1-(v/c)²)
Lorentz úgy képzelte, hogy az erőhatást a Q töltések okozzák, Einstein ezzel nem értett egyet és megpróbált elszakadni a Maxwell féle éteres elgondolás folytatásaként született Lorentz-i megoldástól.
És megírta a "ON THE ELECTRODYNAMICS OF MOVING BODIES
By A. Einstein June 30, 1905"
című dolgozatát, amelynek első mondataiban már tisztázta, hogy Maxwell féle hibás megközelítést szeretné egy jobbal felváltani:
"It is known that Maxwell's electrodynamics--as usually understood at the present time--when applied to moving bodies, leads to asymmetries which do not appear to be inherent in the phenomena. Take, for example, the reciprocal electrodynamic action of a magnet and a conductor. The observable phenomenon here depends only on the relative motion of the conductor and the magnet, whereas the customary view draws a sharp distinction between the two cases in which either the one or the other of these bodies is in motion. For if the magnet is in motion and the conductor at rest, there arises in the neighbourhood of the magnet an electric field with a certain definite energy, producing a current at the places where parts of the conductor are situated. But if the magnet is stationary and the conductor in motion, no electric field arises in the neighbourhood of the magnet. In the conductor, however, we find an electromotive force, to which in itself there is no corresponding energy, but which gives rise--assuming equality of relative motion in the two cases discussed--to electric currents of the same path and intensity as those produced by the electric forces in the former case."
( A folytatást megtaláljátok itt: http://www.fourmilab.ch/etexts/einstein/specrel/www/ )
Einstein nem végzett méréseket, ezért pusztán lemásolta Lorentz függvényeit. Csupán újabb köntösbe bújtatta.
És dolgozatában az új köntösnek megfelelően magyarázta Lorentz eredményeit, függvényeinek alkalmazását.
Sajnos Einstein sem tudott elszakadni az álló éter képzetétől, ezért folyton "stationary system"-et azaz álló rendszert emlegetett.
A kinetikát, a fény relatív sebességét, co-ordináta transzformációkat, tárgyaló első három fejezetben megpróbálta Lorentz munkájától eltérő, pusztán matematikai módszerrel levezetni a ßétát.
Ez nem sikerült neki. Mert kénytelen volt tovább emlegetni az álló és a mozgó rendszerek különbségeit, ezzel gondolatkísérletekre alapozta ezt a matematikai levezetést.
De végül eljutott ő is a ß=1/gyök(1-(v²/c²)) alakhoz.
Majd abból kiindulva, hogy a fény egy pontból R sugáron minden irányban ugyanazon c sebességgel terjed, levezette a relatív egyidejűséget.
Miután Einstein úgy feltételezte, hogy ez a terjedés minden rendszerben azonos, de minden rendszerben másként látható, azaz nem ugyanazon idő és távolság érvényes ezekben a rendszerekben.
Vagyis a viszonyított sebességgel arányban az időnek is viszonyítottnak kell lennie ahhoz, hogy minden rendszerben azonos maradhasson a fény terjedési sebessége.
Természetesen a viszonyított idővel a fény által megtett útszakasz csak akkor képezhet minden rendszerben azonosan állandó c fénysebességet, ha ez az útszakasz hossz is függ a relatív sebességtől.
Ezek után alkalmazta saját elveit a "Maxwell-Hertz Equations for Empty Space." Maxwell függvényekre, a Doppler és a "Ligh aberration" esetekre.
Majd a Lebegyev féle E=m*c² energia egyenérték függvényére, ezzel csupán közös függvénybe hozta össze Lorentz transzformációját, a kinetikai energiát és Lebegyev energia egyenértékét.
Majd éveken át javítgatott ezen a dolgozatán. És 1916-ban megjelentette a Generális teóriáját, azaz az általános relativitásról szóló elképzelését.
Röviden ennyi. Ha valami nem lenne világos, akkor rérdezz és megbeszéljük..
-
Albertus #743 Te jó példa vagy. Te sem érted még a Coriolis erő létrejöttét sem.
" A coriolis-erő NEM jön létre,"
Azt leszámítva, hogy fizikailag létező hatása van a Coriolis erőnek, nézzük, hogy hogyan képződik!
Vegyünk egy forgó korongot és az egyik sugara mentén, egyenes vonalban haladó golyót!
Vizsgáljuk a golyóra ható erőt a korong középpontja felől indulva.
A golyó a tehetetlenségi pályáján egyenes vonalban "szeretne" haladni, de ehhez a korongon ahol éppen van, ahhoz a sugárhoz tartozó kerületről egy nagyobb kerületre kell haladnia, ahol az állandó forgási sebesség (ahogy mondjuk: az állandó körfrekvencia, ) miatt nagyobb kerületi sebesség érvényes.
Tehát a golyó csak úgy haladhat ha közben a mozgására merőleges irányban egyre növekvő sebességgel is halad.
Az időegységre eső sebesség változást gyorsulásnak nevezzük.
Azaz amikor az egyre növekvő sugárhoz, egyre nagyobb kerületen, az egyre nagyobb kerületi sebesség mozdítaná el a golyót a pályájáról,
v1=n*R1*2*Pi/1 kerületi sebességről v2=n*R2*2*Pi/1 kerületi sebességre kell gyorsulnia a(k)= (v2-v1)/1 gyorsulással.
És mint tudjuk a(k) gyorsulás F=a(k)*m erővel hat az m tömegére.
Azaz ha az F erővel érintő irányban hatunk a forgási iránnyal szemben a golyóra akkor megtartja egyenes vonalú mozgását, ha pedig nem hatunk, akkor a kerületi sebesség megváltozásából következő a(k) gyorsulással
fog kitérni a forgás irányába az egyenes vonalú pályájáról.
Ilyen egyszerű..
Persze, hogyan érthetnéd a relativitást, ha még a Coriolis erőről is azt hitted, hogy nem létező..
-
 #742
#742
Paradigmaváltás majd akkor lesz, ha Egely nulltér-generátorát használjuk. 
amúgy meg ja, Einstein egy mai tudományos problémához hozzá sem tudna szagolni.. xDD -
uwu #741 Ez az Einstein fóbiád azért elég szánalmas.
Ennyire fáj, hogy az ő nevéhez fűződik egy paradigmaváltás?
Esetleg az a bajod, hogy nem érted mit alkotott?
Vagy talán az fáj, hogy zsidó volt? -
uwu #740 Igen láttuk.
Pitagorasz tétellel felvértezve estél neki cáfolni a relativitáselméletet. Ehhez kicsit komolyabb matek kellene.
Csak azt sikerült bebizonyítani, hogy nem érted miről szól. Az anomáliák a sajátos értelmezésedből adódtak, valójában az elmélet mást állít mint ami neked lejött belőle. -
 #739
#739
Ugyan már mit vártok tőle? Fel sem tudta fogni, miről szól ez az egész téma, ha értené, nem beszélne ilyen hülyeségeket.
"akik a Coriolis erő létrejöttét sem érti."
Ezek után még akartok tőle valamit? A coriolis-erő NEM jön létre, az egy FIKTÍV erő a vonatkoztatási rendszerek egymáshoz képest elmozdulása miatt... És ez ugye csak a legutóbbi faszsága, majd' minden megnyilvánulásában van egy-két ilyen ordító baromság, én már régen meguntam, hogy folyton helyesbítgessem. Nincs annál rosszabb, mint mikor az ostobaság szorgalommal találkozik... -
lasoabt #738 Na,erre én is kíváncsi lennék.Szerintem még sokan mások. -
kamov #737 Konkrétumokat kértem, nem mellédumát. -
Albertus #736 Már itt is, és több más fórumon is megtettem... lapozz vissza. -
kamov #735 Ha annyira ismered a mögöttes matematikai apparátust akkor toljad szépen a specrel levezetését.. -
Albertus #734 Nem az elvégzett iskolai osztályairól írtam. Hanem arról, hogy milyen ismereteket tanult és milyeneket biztosan nem tudhatott.
A fiam pedig 11 évesen nem csak egy egyenletet tud levezetni, hanem programot ír majd játszunk a progijával. (Most kedett 3D-s animáció programozással foglalkozni.. Na ez még nem megy neki. )
Ami kb ezerszer komolyabb feladat, mint Einstein levezetései.
Ja igen.. Vannak olyan középiskolások is akik még a körmozgásnál tartanak..
Sőt! Még olyan mérnökök is, akik a Coriolis erő létrejöttét sem érti.
-
kamov #733 Meg kellett volna nézni Einstein életrajzát.
1900 kapta meg a diplomáját és 1905-ben szerzett doktori fokozatot.
Csak szólok a mai középiskolás másodikban az egyenletes körmozgásnál tart.
Annyi hogy ő már akkor végig tudott egy egyenletet számolni hiba nélkül...
-
Albertus #732 Albert Einstein azt a teóriáját, amelynek alapján a relatív időt emlegetjük 1905-ben közölte le az a fizikai szaklap aminek Planck volt a főszerkesztője.
Nyilvánvalóan 1905-ben aki nem látott a jövőbe, az nem ismerhette mindazt az alapvető ismeretet amit 1905 után "feldeztek fel".
Azaz történelmi tény, hogy Einstein tudása a specrel megírásakor a mai középiskolás másodikosok tudásszintjét sem érhette el 25 évesen.
Feltételezem, hogy ha ma írna egy másodikból kibukott emberke 25 évesen egy teóriát a relativitásról.. azaz Einsteinnel teljesen azonos tudású emberről van szó, akkor nem vennénk komolyan.
Ne keverjük!
Jelzem, hogy ott volt napi vendég ahol a professzor, a Nobel díjas is csak az 1905 előtti tudomány szintjén volt csak professzor. Nem a mai tudomány szintjén!
-
 #731
#731
Asszem ennek nemigen van köze a témához. És ha Newtonról meg kiderül, hogy buzi volt, akkor a gravitáció már nem működik?
Az meg pláne vicces, hogy azt állítod, hogy "éveken át napi vendég volt a Planck-házban", de ennek ellenére "semmit sem tudott abból amit 1905 után fedeztek fel".
Na, akkor most válassz a két állításod közül egyet, mert a kettő egy csöppet üti egymást. Nyilvánvaló, hogy ha valaki egy Nobel-díjas fizikusnál és egyetemi professzornál napi vendég, akkor az semmit nem hall a tudományos eredményekről. Persze, a Napnál is világosabb... -
Albertus #730 Ezt egy olyan 25 éves emberke teóriája alapján mondják, aki nem tudott felírni egyetlen kémiai képletet sem, aki nem tudta, hogy az áram az áramkörökben merre folyik, aki nem tudta, hogy a mágneses teret a haladó elektron spinje okozza, aki semmit sem tudott abból amit 1905 után fedeztek fel. Nem ismerte Heisenberg, Schrödinger, Feynman, stb. munkáit..
Mamár a középiskola 3. osztályát már nem végezhetné el az 1905-ös tudásával.
Csoda, hogy fogalma sem volt az időről? Totózott.. És szuper jó kapcsolatai voltak. Egy ideig Planck lányával volt "jóban", így majdnem apósa lett a Nobel díjas Planck.. éveken át napi vendég volt a Planck-házban.
Természetesen, így ismerkedett meg az akkori tudományos elit krémjével. Apja sokszoros milliomos, gyártulajdonos volt..
Az ilyenre mondják, hogy életében csak megszületnie volt nehezebb, a többit tálcán kapta.
-
 #729
#729
Az a baj, hogy ez egy nagyon lebutított analógia, és nem nagyon van értelme ezen a szemléleten sokat vergődni. Tehát ezek négydimenziós differenciálegyenlet-rendszerek speciális eseteinek az értelmezései. Meg azt sem szabad elfelejteni, hogy a téridő nem különválasztható térre és időre, hanem egyetlen összefüggő dolog, egyben kell kezelni. A térben haladás egyben időben is haladás, és fordítva.
Nagyjából úgy van, ahogy mondod. Megnézzük a fotont a Napban, újszülött fotonka, 0 másodperc életkorral, eltelik 8 perc, ideér a Földre, megnézzük megint, és ugyanaz az újszülött fotonka, 0 másodperc életkorral. Az ő számára nem telt el idő, egyszerre van mindenhol az útvonalán, miközben a világ elöregszik körülötte.
De ez megint csak elméleti analóg fejtegetés, egy foton korát nem tudjuk vizsgálni, anyag meg soha nem gyorsul fénysebességre.
Mondom, ikerparadoxon, mondjuk wikipedia-n. Ott van egy ábra, abból egész jól látni, miről van szó. Pl azt is, hogy nem csak az odaút és a visszaút okoz időtorzulást, hanem az is, hogy megfordultunk, és vissza akartunk jönni. -
 #728
#728
Miért is kellene gyorsulnia a galaxis forgásának? Igen, nő a központi fekete lyuk tömege, de ennek nincs köze a forgás sebességéhez. Sőt, a galaxis mozgásához gyakorlatilag semmi köze, a galaxis úgyis a saját tömegközéppontja körül forog, annak meg mindegy, hogy pontosan milyen a tömegeloszlás. Lényegtelen, hogy az a tömeg egy pontban gyűlt-e össze(központi fekete lyuk), vagy térfogaton oszlik meg (sűrű csillagvárosok a fekete lyuk körül).
Meg Hawkins szerint a fekete lyukak a pólusaikon sugároznak kifelé. Ha ez így van, akkor nem biztos, hogy pozitív a tömegmérleg, nem biztos, hogy több anyagot nyel el, mint amennyit a kisugárzás miatt veszít. -
 #727
#727
Ha egy foton elindul a napból fénysebességgel gyakorlatilag megáll számára a "saját szempontjából" az idő és ugyanabban a pillanatban érkezik meg a Földre? Vagy hogy értelmezendő? -
 #726
#726
Volt még egy dolog: Aszongya, hogy a fekete lyuk gyakorlatilag tömeggel rendelkező tárgy, amely magához vonzza a kissebb tömegű tárgyakat, meg hogy a galaxisok közepén is fekete lyuk ak vannak, ezzel magyarázzák a spirálgalaxisok mozgását. Akko minél több kissebb tömegű tárgyat vonz magához a fekete lyuk, annál jobban változik a saját tömege is és annál intenzívebben vonzza, tehát "gyorsul" a folyamat? Egyre gyorsabb mozgásra készteti a galaxist? Vagy nem? Nem tudom megfigyeltek-e a spirálgalaxisok mozgásában gyorsulást, pályákban változást. Elméletileg nem kellene gyorsulő folyamatnak lenni, ha a középpont tömege növekszik?