1111
Elgondolkodtató matematikai, logikai feladatok, feladványok
-
#671
mi is büszkék vagyunk rád! ![]()
-
davidragon #670 egyébként a megoldás már tényleg volt korábban, de ez egy nagyon jó kis feladat. Sokat agyaltam rajta annó, és milyen büszke voltam mikor sikerült megoldanom! 
...még mindig az vagyok
-
davidragon #669 ...tehát azt sem tudod hogy a kettő közül melyik a selejt... 
-
#668
ööö azt nem tudom megmondani hogy könnyebb vagy nehezebb mert kizárásos alapon marad 2 golyó úgy hogy billen a mérleg tehát ebből még nem tudom hogy könnyebb vagy nehezebb-e -
#667
de ha 1-1 golyó marad és a mérleg billen, és el tudod dönteni, hogy melyik a selejt, akkor azt is tudod, könnyebb-e, vagy nehezebb.
persze valós a probléma, csak szerintem nem az, amit leírtál. -
#666
igen de baszhatom ha a 3. mérésre tudom kideríteni hogy melyik a selejt mert a végén 1-1 golyó marad és nyilván billen valahova a mérleg jobbra vagy balra. -
#665
ha tudod melyik a selejt, akkor tudod eddig melyik oldalon volt. fent vagy lent.
vagy nem? -
#664
Hmm elkezdtem leírni a megoldást de rájöttem hogy csak azt tudom kideríteni hogy melyik a selejt azt nem hogy könnyebb-e vagy nehezebb-e a többinél mert nem marad a 3 mérésből több lehetőségem :S -
#663
ugyanitt volt:
Van 12 darab egyforma kinézetű golyónk, melyeknek 1 kivételével a tömegük is megegyezik. Megállapítható-e egy kétkarú mérleg segítségével 3 mérésből, hogy melyik golyó a „különc”, és hogy könnyebb vagy nehezebb-e a többinél? Ha igen, hogyan?
de asszem ezt már itt is megoldottuk... -
Dougie #662 én sem tudom mi a helyes megoldás, ezzel a feladattal csak véletlen találkoztam egy oldalon, de érdekelne hogy ki mire jut
voltak ott más feladatok is, pl.
# Hogyan tudunk 2 darab egyenként 1-1 óra alatt elégő gyertya segítségével lemérni 45 percet?
# Hogyan mérhetünk ki egy 7 perces és egy 11 perces homokóra segítségével 15 percet? És ha csak 15 perc áll rendelkezésünkre?
(állítólag a BME Nyílt napján voltak ezek régebben) -
davidragon #661 Majd én számolgatok egy kicsit.
1. Ha kettesével lépkedünk, a törés után pedig egyet lépünk vissza: max 18 dobás
2. Ha hármasával lépkedünk, a törés után pedig egyesével lépünk felfelé az utolsó biztonságos emeletről: max 14 dobás
3. Négyesével: max 12 dobás
4. Ötösével: max 11 dobás
5. Hatosával: max 11 dobás
6. Hetesével: max 11 dobás
7. Nyolcasával: max 11 dobás
8. Kilencesével: max 12 dobás
Tehát 5,6,7,8-asával lépkedve maximum 11 dobásra van szükségünk.
n=lépkedések nagysága
dobás = 36 mod n + n - 1
Ha hibás a számolás szóljatok. -
#660
jelöljünk:
az utolsó ismert biztonságos emelet: b.
ha csak egy tojás lenne, akkor mi lenne?
b: biztonságos.
b+1: kipróbálható, legfeljebb törik és akkor b az eredmény.
b+2: ha kipróbáljuk és törik, akkor nem tudjuk, hogy b+1 jó lett volna-e.
tehát egy tojással egyet léphetünk.
két tojással?
több lehetőség van.
1: kockáztatunk és felmegyünk valameddig,(pl) feléig. dobunk, ha nem törik, irány felfelé a 3/4-ig stb, amíg nem törik. ztán az első törésnél az utolsó biztonságosról fellépdelünk egyesével.
2: ha nem a feléig, hanem valahanyad részéig megyünk elsőre, aztán ha törik, egyesével araszolunk.
3: biztosra megyünk és kettőt lépünk fel, egyiket dobjuk, ha törik, akkor b+1-ről a másikat, így b, b+1, b+2 mérve van, tehát tudjuk.
értékeljük.
1: legrosszabb eset, ha feléről (18) törik és egyesével kell felmásznunk a 17-ikre, így 18-at dobtunk.
2: ?
3: a legrosszabb esttben a tető alá (b=36, vagy 37) megyünk, kettesével, vagyis 18+1=19-et dobunk.
a megoldás valószínűleg a 2-es rajtszámnál van, de sajna nincs több időm...
-
Dougie #659 A strucctojás rendelkezik egy olyan tulajdonsággal, hogy egy bizonyos magasságról leejtve összetörik, alacsonyabbról viszont akárhányszor leejthető, sértetlen marad. A strucctojások egyformák. A feladat: két tojás segítségével határozzuk meg egy 36 emeletes házban a strucctojás összetörésének határmagasságát (melyik az az emelet, ahonnan még le lehet dobni úgy, hogy egészben maradjon, de magasabbról már nem). A tojásokat össze is törhetjük, de a második összetörése után már választ kell adnunk. Adjunk olyan módszert, amely a lehető legkevesebb lépésben garantáltan választ tud adni (vagyis minimalizálandó a kísérletek száma a legrosszabbb esetre). -
#658
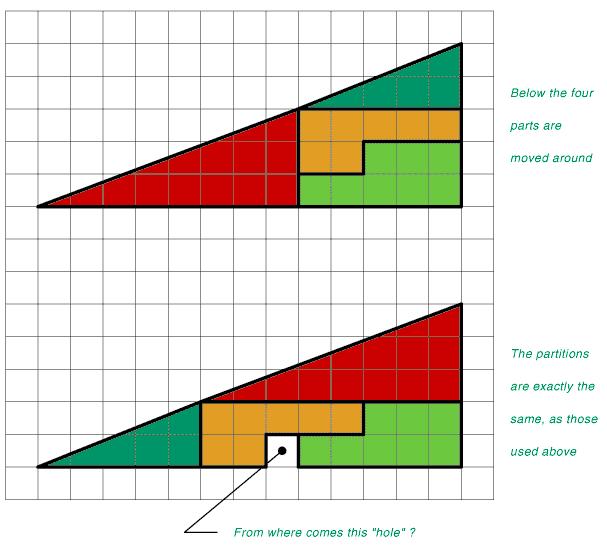
Igaz, hogy volt, de jó, hogy újra betetted, mert a megoldás igazi miértjéről nem esett bővebben szó...
Megfigyeltem, hogy ugyanezt a feladatot el lehet készíteni többféle méretben is. De csak akkor működik, ha a háromszögek oldalai kettővel egymásutáni fibonaccik. Tehát a lenti esetben is erről van szó, mert mindkét háromszög fibonacci oldalakkal bír: 5:2 és 8:3. Ha sorba teszed, akkor: 2, 3, 5, 8 fibonacci-sor részletet kapod.
Érdekes nem?! -
#657
Helyes.
SPOILER! Kattints ide a szöveg elolvasásához!Tehát a fenti képen összekötve a felső sarkot és a bal alsó sarkot egy akkora területű háromszög van, mint a lenti négyzet. A rácsozás azonnal adja a megoldást, mert elsőre szemet szúr, hogy nem azonos a meredekség... -
Dougie #656 már volt #443 környékén -
davidragon #655 SPOILER! Kattints ide a szöveg elolvasásához!Amire én gondolok, hogy ez valójában nem is háromszög, mert a piros és zöld háromszög szöge nem egyenlő, és ez okoz alul többletet. -
davidragon #654 Ezt ismeritek?
Ha valaki tudja mi a megoldás, én kíváncsi lennék.
![]()
-
pet0330 #653 -t:)
-
pet0330 #652 Freizetit te hanyadikos vagy? -
#651
nem. -
Thanatos #650 ne velünk odlasd meg az általános iskolás házidat pls :) -
freizeit #649 S.O.S.
Adott egy 30fokos szög, szárai között pedig egy P pont.
Szerkessz egy 5cm-es szakaszt, mely áthalad a P ponton és végpontjai 1-1 szögszáron fekszenek.
Már egy hete ezzel kínlódom, nem tudom megoldani, segítsetek! -
#648
Aranyos játék...
SPOILER! Kattints ide a szöveg elolvasásához!
1. 2k-1k
(átmegy 2 kannibál; kiszál 1, 1 visszamegy)
2. 2k-1k
(átmegy 2 kannibál; kiszál 1, 1 visszamegy)
3. 2p-1p+1k
(átmegy 2 pap; kiszál 1, 1 kannibál visszamegy)
4. 2p-2p+1k
(átmegy 2 pap; kiszál 2, 1 kannibál visszamegy)
5. 2k-1k
(átmegy 2 kannibál; kiszál 1, 1 visszamegy)
6. 2k-2k
(átmegy 2 kannibál; kiszál 2)
-
n3whous3 #647 Ezt az űberláma megfogalmazást :D A sötétség a fény HIÁNYA. És egy anyag nem fényhordozó, jóisten miket beszéltek már... egyszerűen visszaveri a fényt az anyagmutatója szerint és csecs... :D -
davidragon #646 hehe, nem rossz! de a kannibáloknak is át kell érniük, akkor van vége a játéknak. -
blackgamer #645 küldjed át a három misszionáriust a túlpartra, de vigyázz, mert a kannibálok megeszik őket ha többen vannak
link -
#644
Látjátok,értek én a szép
szóból is! -
#643
ezt akartam leírni csak nekem velősebben sikerült :D -
Thanatos #642 igaz, nem hülye vagy, csak simán nem ide vágóak a krédéseid, ez a topik logikai, matematikai godnolkodtató feladatoknak van, és nem pedig kémiai fizikai ismeretek tárgyalására, beirhatna neked bárki atomfizikábol kérdést pl, attol az még nem elgondolkodtató hanem vagy tanutlad/olvastál róla vagy nem, az itteni kérdéseket viszont 8 általánossal is ugyan olyan könnyü vagy nehéz leeht megoldani mint 6 diplomával mivel nem a szigoru lexikális tudás a lényegük hanem pont hogy józan paraszti ész kell csak hozzájuk és/vagy nem a szokásos általános godnolkodásmod (tudod, think out of the box...)
szóval nem rossz krédések csak nem ide valóak, ennyi -
#641
Igen,nagyvonalakban.
Na nem kérdezek többet,nem szeretem
ha lehülyéznek (#633)! -
#640
Ezt nem tudom, de van egy tippem:
SPOILER! Kattints ide a szöveg elolvasásához!A sötétből lesz a világos, mivel a fényt csak úgy tudjuk látni, ha az az anyag, amit előtte nem láttunk a fény hiánya miatt, most "fényhordozóvá válik". -
#639
Igen, ez a helyes megoldás. -
#638
SPOILER! Kattints ide a szöveg elolvasásához!Az egyik láncon az összes szemet megbontjuk és azzal összekapcsoljuk a maradék három láncot... -
#637
NADE KÉRLEK! -
Axl Rose #636 [spoiler] Esetleg Alexandra részéről egy pipa az ékszerésznek ? 
[spoiler]
-
#635
Remélem a Painttel improvizált rajzomom látszik nagyjából a lényeg.... 
-
#634
Alexandrának volt négy darab aranylánca, és mindegyik darab 3 láncszemből állt. Össze akarja a darabokat állíttatni egyetlen kör alakú lánccá, de fél, hogy nem lesz elég a pénze.
Az ékszerész szemügyre veszi a láncdarabokat.
- Egy tallért számítok egy láncszem megbontásáért, és egy tallért azért, hogy újból összeforrasztom. Hogy összeíllítsam a darabokat, mindegyiken egy-egy szemet kell megbontanom és összeforrasztanom. Így kapcsolom egyik láncdarabot a másikhoz. Ez összesen 4 láncszem megbontását jelenti, 8 tallérba kerül.
Azonban Alexandrának csak 7 tallérja volt.
- Nincs elég pénzem - mondta szomorúan. - Pedig abban reménykedtem, hogy ma este már felvhetem ezt a nyakláncot. De hát ez nem érdekes...
Alexandra összeszedte a darabokat, és kifelé indult az üzletből.
Az ékszerész utánaszólt:
- Várjon! Kigondoltam valami mást
Hogyan lehet a láncot olcsóbban összerakni?
![]()
-
#633
elbújik a fény mögé! van még egyébb hülye kérdésed? -
#632
Így ahogy mondod.
És ha éjszaka bemész a szobába,felkapcsolod a lampiont,
hova lesz a sötét?
