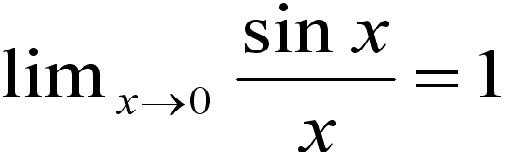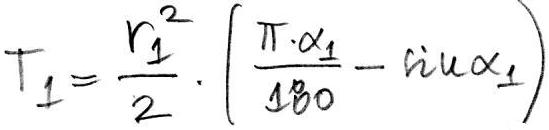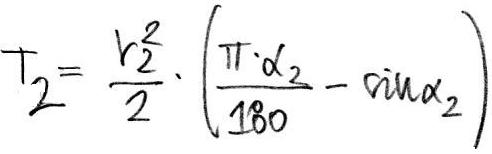4415
Matematika feladatok
-
 #772
#772
ő a szinuszra/koszinuszra értette, nekem legalábbis úgy tűnt... én vegyipariba jártam, ott középsuliban bevezettek az analízis rejtelmeibe matekból is...
-=ZR=- -
knadam #771 Fősuli Kecskemét GAMF kar! Én középsuliba nem tanultam ilyen magasröptű dolgokat! -
 #770
#770
középsuliban :) nem annyira borzasztó és milyen hasznos! :P loál
-=ZR=- -
Bammy #769 Ezt a sinus cosinust középsuliban tanítják? Vagy csak egyetemen? Meg amikről itt beszéltek...így külső szemmel elég durvának néznek ki, mondjuk mindne a matekbasn, de aztán meglehet érteni. Mondjuk én mérnökire szeretnék menni, igaz csak 4-es vok matekból, mert a kis apró figyelmetlenségekből mindig összegyűlik 2-3 pont minusz ami miatt nincs meg az ötös :( :) -
knadam #768 Igen ma lett volna és tényleg -2 lett! Kijavították a nagy zh-t és összesen annyi pontom lett ami a hármasra elég! De ha 2 feladatot bemutatnék akkor 4 is lehetnék! Thibi esetleg msn címet nem tudnál adni? Adott fel megint vagy 5 feladatot! 3 függvényábrazolás, meg vagy 2 szakadási hely, azt hiszem! -
Thibi #767 Ez a holap reggel ma délelőtt volt?
mivel sin(x)/x határértéke x=0-nál 1, az x/sin(x) határértéke is 1,
ezért (x-pi)/sin(x-pi) határértéke x=pi esetén 1, (x-pi)/-sin(x-pi) hátárértéke pedig -1, és az 1-cos(x) értéke x=pi-nél 2, így a teljes függvény határértéke -1*2=-2 -
knadam #766 762re gondolok természetesen! :D -
knadam #765 A 722-t be tudnád azért fejezni nekem? A másik tiszta! Köszönöm! Holnap reggel 9:35től mutatom meg a tanáromnak! Szóval ha addig írsz az nagyon jó! -
Thibi #764 a negyedik sorban a *)= rész törlendő -
Thibi #763 A másik meg -5 lehet:
x*(ln(x-5)-ln(x))=x*ln((x-5)/x)=ln(((x-5)/x)^x)=ln(((1-5/x)^x)
ha minden igaz,akkor az (1+a/x)^x hatértéke: e^a ,ezért -5 lesz a határérték -
Thibi #762 Az első talán -2:
mivel azt hiszem sin(x)=-sin(x-pi)
és mivel a függvénytáblázat szerint tan(x/2)=(1-cos(x))/sin(x),ezért
(x-pi)*tan(x/2)=(x-pi)*)=(1-cos(x))/sin(x)=(x-pi)*(1-cos(x))/-sin(x-pi)=
=(x-pi)/-sin(x-pi)*(1-cos(x))
innen már csak tudod -
knadam #761 Csütörtökre kellenének a feladatok! Ha nem tudtok segíteni akkor megpróbálom egyedül! Ezt nem hagyhatjátok... -
knadam #760 A 754-es hszben lévő 2 feladatnak kellene! Köszi! -
#759
Kell ennek a levezetése? -
knadam #758 -
knadam #757 Analízis 1-nél most nem veszünk még deriválást! Beírom a képletet amit kellene használni hozzájuk, de az órán vett pédák nem voltak ilyen húzósak! Mindkét feladat 5-5 pontot ér ha órán le tudom vezetni és mivel harmadjára veszem fel a tárgyat égető szükségem lesz minden egyes pontra a végelszámolásnál! Most jut eszembe, hogy van otthon valamelyik polc mélyén egy t10-es...
-
ugot2know #756 tg-t írd át ctg-be és L'Hospital-szabállyal dolgozz tovább!
Másodiknál is vszinű törtté kell alakitani az x-ből lesz a nevező (1/x)... -
 #755
#755
nem emlékszem pontosan, de mintha deriválni kéne a nullászor végtelen alakút és akkor kijön, hogy nullább-e mint végtelen, vagy fordítva. -
knadam #754
Most hátha jó! -
knadam #753
Please help me!
-
knadam #752 Analízisből lenne 2 feladat amiben a segítségeteket kérném! Függvény határértékét kell kiszámolni! Este ha hazaértem beszúrom a feladatokat! Előre is köszi! -
 #751
SPOILER! Kattints ide a szöveg elolvasásához!
#751
SPOILER! Kattints ide a szöveg elolvasásához!
Ezért a szép numerikus megoldásért cserébe arra kérek mindenkit, túrja meg otthon a fiókokat és ha kezébe akad egy működő 16 bites PCMCIA LAN kártya, azt adja el nekem baráti áron! Köszönöm! PI-es laptopba lesz! Ha valaki régi Ericsson telefonnal akad össze, szintúgy jelezze azonnal! Justin, amúgy is lógsz nekem effélével, ha jól emlékszem! ;)
Ha vki numerikus matekról akar csevegni, vagy hogy milyen számológépet érdemes manapság venni, akkor azt is belefér egy ilyen topicba, asszem - elvégre a matematika az alkalmazásaiban mutatja meg a valódi erejét! ;)
-=ZR=- -
 #750
#750
A másik kettővel pedig - valszeg most fog menni:
Tehát az elejétől:
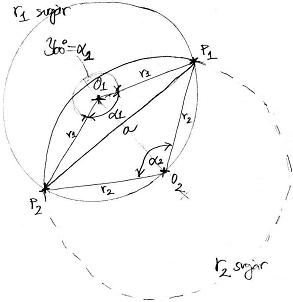
A kecske, aki jobb lenne ha birka lenne, az r2 sugarú körön tud mozogni, aminek a középpontja O2 és ez a pont rajta fekszik az r1 sugarú O1 középpontú rét kerületén:
Ha jobban megvizslatjuk az első ábrát, az 'a' hosszúságú szakasz éppen 2 körszeletet metsz ki a két kör közös részéből - azt két körszeletre osztja, pontosabban:
Azt kell még itt észrevenni, hogy a két középpontnál jelölt alfa1 és alfa2 szögek között fennáll az alábbi kapcsolat:
merthogy kerületi és középponti szögekről van szó.
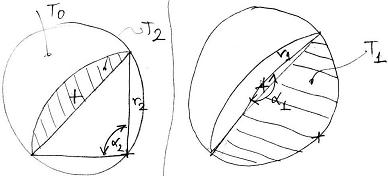
Namost egy körszelet területe számolható úgy, hogy:
és a másik pedig:
A fenti két egyenletet összeadva szépen kapunk egy területet, amit leosztva a rét területével (r1^2*PI) a kapott egyenletet 1/2-del egyenlővé téve meg kell oldani r2/r1-re.
Ami nem is olyan trivi.
Meg nehéz is.
Még ha áttérünk radiánra és a PI*alfa/180 tagok helyére mindenütt beírhatjuk azt, hogy alfa, mert ez csak erre volt jó (a Bronstejn szereti a fokokat, valszeg).
Én azt a módszert választottam, hogy előszedtem az egyik - a felvételinél használt és igencsak kedvelt - zsebszámológépemet és kihasználva, hogy van rajta SOLVER, megírtam neki a területarányt számoló algoritmust egy kis programba és asszontam, hogy na, ezt oldjuk meg a két sugár arányára.
[...stb...]
-=ZR=- -
 #749
#749
Tehát az elejétől:
A kecske, aki jobb lenne ha birka lenne, az r2 sugarú körön tud mozogni, aminek a középpontja O2 és ez a pont rajta fekszik az r1 sugarú O1 középpontú rét kerületén:
Ha jobban megvizslatjuk az első ábrát, az 'a' hosszúságú szakasz éppen 2 körszeletet metsz ki a két kör közös részéből - azt két körszeletre osztja, pontosabban:
Azt kell még itt észrevenni, hogy a két középpontnál jelölt alfa1 és alfa2 szögek között fennáll az alábbi kapcsolat:
merthogy kerületi és középponti szögekről van szó.
Namost egy körszelet területe számolható úgy, hogy:
és a másik pedig:
A fenti két egyenletet összeadva szépen kapunk egy területet, amit leosztva a rét területével (r1^2*PI) a kapott egyenletet 1/2-del egyenlővé téve meg kell oldani r2/r1-re.
Ami nem is olyan trivi.
Meg nehéz is.
Még ha áttérünk radiánra és a PI*alfa/180 tagok helyére mindenütt beírhatjuk azt, hogy alfa, mert ez csak erre volt jó (a Bronstejn szereti a fokokat, valszeg).
Én azt a módszert választottam, hogy előszedtem az egyik - a felvételinél használt és igencsak kedvelt - zsebszámológépemet és kihasználva, hogy van rajta SOLVER, megírtam neki a területarányt számoló algoritmust egy kis programba és asszontam, hogy na, ezt oldjuk meg a két sugár arányára.
[...stb...]
-=ZR=- -
 #748
#748
persze a képeket nem rakja bele..., na mégegyszer...! -
 #747
#747
Tehát az elejétől:
A kecske, aki jobb lenne ha birka lenne, az r2 sugarú körön tud mozogni, aminek a középpontja O2 és ez a pont rajta fekszik az r1 sugarú O1 középpontú rét kerületén:
Ha jobban megvizslatjuk az első ábrát, az 'a' hosszúságú szakasz éppen 2 körszeletet metsz ki a két kör közös részéből - azt két körszeletre osztja, pontosabban:
Azt kell még itt észrevenni, hogy a két középpontnál jelölt alfa1 és alfa2 szögek között fennáll az alábbi kapcsolat:
merthogy kerületi és középponti szögekről van szó.
Namost egy körszelet területe számolható úgy, hogy:
és a másik pedig:
A fenti két egyenletet összeadva szépen kapunk egy területet, amit leosztva a rét területével (r1^2*PI) a kapott egyenletet 1/2-del egyenlővé téve meg kell oldani r2/r1-re.
Ami nem is olyan trivi.
Meg nehéz is.
Még ha áttérünk radiánra és a PI*alfa/180 tagok helyére mindenütt beírhatjuk azt, hogy alfa, mert ez csak erre volt jó (a Bronstejn szereti a fokokat, valszeg).
Én azt a módszert választottam, hogy előszedtem az egyik - a felvételinél használt és igencsak kedvelt - zsebszámológépemet és kihasználva, hogy van rajta SOLVER, megírtam neki a területarányt számoló algoritmust egy kis programba és asszontam, hogy na, ezt oldjuk meg a két sugár arányára.
A számológép így fest:
A rövidke program pedig:
LBL K
RCL K ; k itt r2/r1-et jelöli
2 ;
/ ;
ASIN ;
2 ;
* ; alfa1 számítása: alfa1=2*arcsin(k/2)
STO A
2
/
+/-
PI
+ ; alfa2
STO B
RCL A
ENTER
SIN
-
2
/ ; T1 számítása
RCL B
ENTER
SIN
-
2
/
RCL K
X^2
* ; T2 számítása
+ ; T1+T2 számítása
PI
/ ; (T1+T2)/T_rét számítása (T_rét=PI, egységsugarú!)
2
1/X
- ; itt pedig levonjuk az 1/2-et, hogy F(r2/r1)=0 alakú legyen az egyenlet!
RTN
54.0 BYTE
CK=EC52
A használata pedig:
FN= K
1 STO K
2
SOLVE K
eredményképpen pedig a már említett r2/r1=K=1.2212 értéket kapjuk.
Fontos, hogy a számoló RAD módban legyen!
-=ZR=- -
 #746
#746
;) mérnökként én is gondolkodtam, hogy van-e értelme, de aztán rábólintottam magamban, mondván: nem gyakorlati a feladat (hacsak valaki meg nem csinálja...)
-=ZR=- -
 #745
#745
részleteket! -
#744
Elég pontos ez? :D:D:D -
 #743
#743
A fene...
A kecske póráz hossz/rét sugara = 1.22121589912
EZ A JÓ!!!
-=ZR=- -
 #742
#742
A rét sugara/kecske póráz hossz = 1.22121589912 a részletek hamarosan!
-=ZR=- -
 #741
#741
Sziasztok!
Van egy trükkös feladatom, amivel nem jutottam semmire. Ha valakinek van ötlete, írjon! Elég lenne annyi is, ha adnátok vmi ötletet, hogy merre induljak el.
A feladat:
A szumma(1/n) sor divergens. Most hagyjuk el ebből a sorból azokat a tagokat, amik nevezőjének tízes számrendszerbeli alakjában a 9-es szám szerepel. Állítás: Ez a sor konvergens. Mennyi a sorösszeg? -
 #740
#740
elte.hu
felvi.hu
telefon, stb. -
della #739 Én még gimnáiumba járok csak, de nem sokára értettségizem, az ELTE - Matematika alapszakára készülök, és ahogy néztem a 3 év után(Bsc) 4 szakitány(Msc) közül lehet választani. A matektanáron kívül a másik 3ról - elméleti matematikus, alkalmazott matematikus,elemző matematikus - szeretnék kérdezni, hogy mivel foglalkozik ez a 3 ág, és hol és miként tud elhelyezkedni az, aki e 3 szak valamelyikén szerzett diplomát. Remélem tud valaki bővebb információt adni ezekkel kapcsolatban.
Előre is nagyon köszönöm. -
della #738 A szögfüggvények (sin, cos) 10.-es tananyagok, szóval a kombinatorika után ez jön elvileg:) -
#737
Engem is érdekelne a feladat (grafikus) megoldása. Aztán szép rajz legyen! :D -
Bammy #736 Ezeket a sin meg cos meg tan meg ctg cuccokat mikor tanulja az ember középsuliban? -
TomBond #735 Naná hogy érdekel! -
 #734
#734
hoogyne!, pont olyan vagyok! ;) akkor már tudom, mi volt az a félmosoly, amikor összefutottunk ;) akkor még nem olvastam a fórumot!
-=ZR=-
ui.: ha még éget valakit a felet legelő kecske problémája, akkor a nagyközönség elé tárom, csak csinálok hozzá szép rajzot -
#733
Pályaválasztási tanácsadónak készülsz? :)