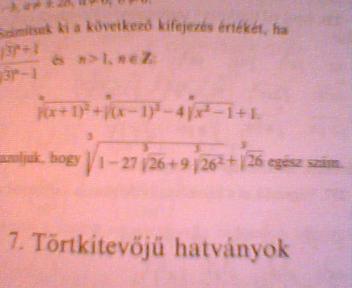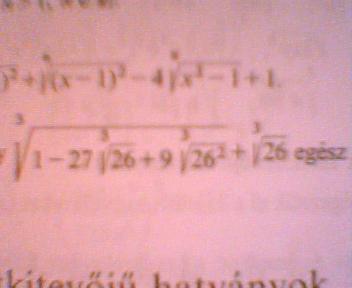4415
Matematika feladatok
-
#732
sztem nyugodtan menj alkalmazott matematikusnak a BME-re vagy ha jobban fog tetszeni, az ELTE-re. aztán válaszd be a "pánzügyi matematika" szakirányt, menj el egy vezető pénzintézethez elemzőnek, ha a nyári időszakokat kihasználod, nameg az évközbeni kevésbé hajtós szakaszokat, tudsz annyi pénz összeszedni, hogy röhögve fizeted minden költségedet év közben és megismer az adott bank is téged, te meg gyakorlatot szerzel. Nyelvvizsgára nagyon rágyúrni, mert bele lehet bukni, ha nincs meg. ezután egyenes a pálya, ha jól muzsikáltál. rongyosra keresheted magad, ha tényleg jó vagy és ha banki szférában fogsz elhelyezkedni, mindíg hitelképes leszel ;) , de meglehet, nem lesz rá szükséged, ha a GDP kormányváltástól független alakulását meg tudod becsülni előre ;)
-=ZR=- -
#731
én má több mint tíz éve érettségiztem, szóval fogalmam sincs, de asszem erre van a felvi.hu -
Bammy #730 És ha pl műszakira szeretnék menni akkor muszáj emelt szintű matek érettséit tennem, vagy elég simát és van még egy felvételi?
vagy tegyök fel a KÖZGAZ-nál? Mert a közgazdaságtan még érdekel is. -
#729
Vannak olyan 6 osztályos gimnázium ahol kevésbé figyelnek oda a meglévő (5. év végi, 6. félévi) jegyekre, tehát ahol csak az számít hogy írod meg a felvételit? -
#728
bármelyik műszaki kar erősen épít a matekra.
elvileg. sajnos elvileg. úgy értem van ahol elhanyagolják, pedig szerintem nem kéne. -
Bammy #727 Srácok lenne egy kérdésem! Ti látom nagy matekosok vagytok. Az a helyzet hogy 10.-es vagyok egy gimnáziumban, elég jó vagyok, mindenből 4-es kivéve idegen nyelvek 5-ös. De egyáltalán semmi elképzelésem hogy merrefele menjek majd, és különösen nicns ami érdekelne, egyedül a matek. És az jól is megy. Szal most úgy vagyokhogy hajtom a matekot mert ezt szeretném használni, néázelődtem már de milyen egytemek vannak amire nyert utad van szinte ha nagy matek agy vagy? Tudom ez hülye skéréds, kérdzehetném úgyis hogy melyek azok az egyetemek amelyekhez a matek kell leginkább. ja és ha ilyenre akarok menni akkor muszáj matekból emelt szintű érettségit tennem? -
#726
megoldottam már. 40 fí-je 100. és így könnyen ki lehetett számolni :) -
#725
Ez valami olyan binomiális tételes-kifejtőssé visszavezethető ;) csak 3 tag összegének a hatványát kell megvizsgálgatni, mik maradnak a végén... Lehet, hogy a
(10*b + c)^n = valamivalami + (10*b)^2*c^(n-2) + (10*b)^1*c^(n-1) + c^n
tapasztalatait felhasználva már az utolsó tagokból meg fogod tudni mondani, milyen jegyek jöhetnek szóba az utolsó kettő helyiérték helyén. Itt elegendő az utolsó két tagot nézegetni (10*b)^1*c^(n-1) + c^n, amiből rögvest ki lehet találni, hogy az utolsó előtti tag csak a tizesekbe szól bele, a legutolsó c^n pedig a tizeseket és az egyeseket befolyásolja. Hasonló eredményt fogsz kapni 3 tag esetén is.
Mindent bele! ;)
-=ZR=- -
Thibi #724 Az utolsó két számjegy által alkotott szám hatványait kell vizsgálni, egy idő után elkezd ismétlődni,illetve elég az eredmény számok utolsó két jegyét szorozgatni az eredeti kétjegyű számmal (maximum 50 után biztos ismétlődni fog) -
#723
nagy számok (százas nagyságrendű) nagy kitevőjű hatványainak (százas nagyságrendű) uccsó két számjegyét hogy kell kiszámolni??? -
7evenb #722 így talán jobban látszik:
|bn| <= (|a1|+...+|an|)/n = (|a1|+...+|an0|+|a{n0+1}|+...|an|)/n <= (n0*K+(n-n0)*d)/n <= n0*K/n+d
-
7evenb #721 an konvergens, tehát korlátos. legyen ez a korlát K, sőt teszőleg d>0 számra létezik olyan n0 index, hogy |an|<d minden n>n0-ra. Ekkor
|bn| <= (|a1|+...+|an|)/n = (|a1|+...+|an0|+|a{n0+1}|+...|an|)/n <=
<=(n0*K+(n-n0)*d)/n <= n0*K/n+d
-
#720
az (a1+a2+a3+...+an)/n kifejezés tulajdonképpen a számtani közép, vagyis ...
és akkor itt lett volna még néhány ötletem, de sorra megcáfoltam.
viszont.
legyen a(i)=1/gyök(i) [i=1..inf]
ez nullához tart, ugye?
és szumma a(i) végtelenhez.
akkor b(i) limeszénél végtelen per végtelen, de a felső négyzetes (?)
tehát a limesz nem nullához tart.
ha az a(i) -nél a négyzetgyök "kevés" akkor legyen köbgyök, vagy mégtöbbedik.
tudom, hogy nem egzakt amit írok, de nekem az az érzésem, hogy egy olyan összefüggést akarunk bizonyítani ami nem mindig igaz. ha pedig így van, (vagyis csak néha illetve általában igaz) akkor nem bizinyítható.
remélem sikerült ötletet adnom azoknak, akik egy konkrét példával cáfolják meg az állítást, vagy esetleg az én logikai bukfencem ad ötletet nekik a bizonyításhoz...
-
#719
azért örülük, hogy így hét év távlatában még be is ugrott elsőre!, annak viszont nem, hogy csak ennyit tudtam segíteni :((( Akkor lehet tovább agyalni!
-=ZR=- -
#718
Öö az a helyzet, hogy az, hogy egy 0-hoz tartó sorozatból sort képzek (vagyis a sor általános tagjaiból képzett sorozat a nullához tart), csak szükséges, de nem elégséges feltétele annak, hogy maga a sor konvergens legyen és a sorösszeg véges szám legyen. Szóval az, hogy an->0-hoz, még nem jelenti azt, hogy a1+a2+...+an egy valós számmal egyenlő.
Amit írtál, az pedig a Leibniz-kritérium, ami azt mondja ki, hogy alternáló soroknál, ha az általános tagok abszolútértékeiből képzett sorozat monoton fogyóan tart a nullához, akkor a sor konvergens. De nem tudjuk, hogy an alternáló. -
#717
azt kellene bebizonyítani, ha van egy sorozatod, aminek a határértéke 0 és ebből sort képzel, akkor annak véges szám a határértéke. Mert ez van bn számlálójában. Ha ez sikerül, akkor ez egy sima sorozat, ami "szám/n" alakú, aminek a határértéke már vizslatható, hogy 0.
Van vmilyen kritérium 3db, erre: legyen an alternáló, tartson 0-hoz, meg nemtommi. valami L-betűs??? csáveszhez köthető ez... Ilyen maradéktagos-mókás témakörnél került elő... ;)
-=ZR=- -
#716
Sziasztok, kérnék egy kis helpet:
Van két sorozat, a következőket tudjuk róluk:
lim (an) = 0
bn = (a1+a2+a3+...+an)/n
Be kell bizonyítani, hogy bn is nullához tart. Van vkinek ötlete? próbáltam átalakítani, hogy egy korlátos és egy nullához tartó sorozat szorzata legyen, de nem jött be. -
#715
A primszámokról (köztük a Fermat féléről is!) bővebben itt. -
manwe #714 meg tudná nekem mondani valaki h mi az a fermat féle törzsszám? meg h mit jelent az h álprím, azt olvastam h bólyai fedezte fel h a 341 álprím, a fermat féle törzsszámhoz meg úgy jutottam h gauss életéről olvastam és ott ha jól emléxek írták h rájött h csak azok a szabályos négyszögek megszerkeszthetők amelyek oldalai fermat féle törzsszámok pl. 3,17,65537 -
#713
Igen igy mar stimmel :) -
Thibi #712 akkor 4 a megoldás,ha ez volt a feladat:
3^(3^x)=27^27 -
#711
tehat 3 a 12en az = 27 a 27en nah ez hulyeseg szara megoldas... -
Realtibi #710 ez a sárgában /matematika feladat gy./
4. fej
1084/b kérdése
és hátul 4 et ir megoldásnak
-
#709
nem 81et ir hatul? -
Realtibi #708 ez egy expéorenciális egyenlet
3 a 3x. en = 27 a 27 diken
na most ebböl az van hogy
27 az x ediken = 27 a 27 .en
szal x= 27
én igy számolnám de a könyvem más eredményt ir hátul
valami 5 let?? -
Realtibi #707 kösz -
#706
(gyokx-gyok2)a negyzeten (gyokx-gyok3)a negyzeten =0
innestol mar csak vizsgalgatni kell -
Realtibi #705 (x- gyökx-2 - 2) ( x- gyökx-3 - 3)= 0
ennek mi a megoldása
légyszi segitsetek
elöre is kösz -
#704
megint segített a topik... 
-
#703
Má rájöttem :D -
#702
Kéne egy kis segítség :)
Írjuk fel prímtényezők szorzataként az alábbi számokat:
6 a négyzeten szorozva 10 a harmadikon szorozva 15-el...
-
#701
Spk hallgatónak szerencsére életében nem kell alkalmaznia azt a sok elméletet amit beletömnek kicsi fejébe. -
#700
Én nem is arra értem, hogy egy száraz matematikai fogalmat bohócjelmezben kell előadni, hanem megmutatni, hogyan kapcsolódik ez a "való világhoz". Azt gondolom, a matematika az alkalmazásaiban mutatja meg az igazi "erejét", de ezt elfelejtik az oktatás során.
Sok hallgató megtanulja az analízist, de hogy ezt tudná is használni valamire a való életben, az igazán ritka. (Hogy az első lépésről, a jó modellalkotásról ne is beszéljünk...!)
A másik sajnálatos véglet, hogy szabályokat tanulnak a hallgatók, de nem tudják a hozzátartozó elméletet, így akkor is akarják alkalmazni a tanultakat, amikor nem lehet. Ezt a tanulást is lehet a száraz anyag bebifláztatásán túl segíteni némi élvezetesebbé tevő gyakorlati alkalmazással.
-=ZR=- -
#699
Rég láttam ilyen hülye commentet. Ha van egy matematikai definíció, akkor azt nem lehet máshogy, érdekesen elmondani. Amúgy meg sokaknak, ez is érdekes lehet. -
Realtibi #698 opsz
nem figyeltem hogy valaki már megoldotta:D
-
Realtibi #697 azért leirom:D
na a léyneg az hogy a 3. gyök alatti kifejezés egy köb
szal igy fog kinézni=
3.gyök alatt (3-3.gyök26)a köbön /itt vége van a 3. gyökön alattnak/ + 3.gyök 26=
3-3.gyök26+3.gyök26=3
parancsolj
bocs hogy igy betüsen irtam de még nem jöttem rá hogy lehet itt gyökölni:D -
Realtibi #696 de mákod van
pont ezt csináltuk ma:D -
Thibi #695 A köbgyök alatti kifejezés (3- harmadik gyök 26) a harmadikon-nak felel meg. Ez alapján az egész kifejezés értéke 3,ami egész szám. -
#694
ha látnám... -
#693
Valaki segítsen ha tud, holnapra kéne számolással együtt.
![]()
![]()
