4415
Matematika feladatok
-
TomBond #652 Ennek már általános iskolában sem kéne hogy gondot okozzon. -
 #651
#651
Te most komolyan mondod, hogy "18-25 között"-i korcsoportban ez a feladat még kihívást jelent számodra? Vagy csak elírtad a születési dátumodat? -
 #650
#650
okmár segitettek msn-en!
A megoldás a hozzáértöknek:
"a" oldal kiszámitásának a képlete: cnégyzet böl bnégyzet=anégyzet -
 #649
#649
-
 #648
#648
Hy
Kérem segitsen valaki!
Matek dogám lessz,és egy valamit nem tudok!
Itt ez a 3szög!
Ha a "c" oldala van megadva,és "b",akkor az "a" oldalát hogyan lehet kiszámitani Pitagorász tétel alkalmazásával?
Ha az "a" és a "b" van megadva akkor azt tudom,hogy a "c" oldalát hogyan kell kiszámolni!
Azt is tudom azt hogy kell,ha a "b" oldala hiányzik!
Ezeket az eredményeket szerkesztéssel le is ellenőriztem,és jo lett a végeredmény!
De ha az "a" oldalát akarom kiszámitani,akkor so se jön össze!
Igazábol az "a" oldal kiszámitásának képletére lennék kiváncsi,ha a "b" és a "c" oldal meg van adva! -
steweee #647 azért mert ilyen topic nincs külön hogy flashget, és gondoltam talán itt tudja rá vki a választ minthogy ez matematika. (excelt tanultam) mindjárt kipróbálom, és köszi a választ -
 #646
#646
.[0-9][0-9][0-9]
De nem értem, hogy ezt miért a matek feladatok topikba kellett. -
steweee #645 azt hogyan tudnám meg beleírni a flashget letöltés / beállítások sorába hogy az ***.01 től az ***.100 ig vagy végtelenig kijelölje az ilyen fájldarabokat letöltés gyanánt. a többi típust be tudom állítani pl : .nfo;.sfv;.r01;.ZIP;.EXE;.BIN;.GZ;.Z;.TAR;.ARJ;.LZH;.A[0-9]?;.RAR;.R[0-9]?
játékokhoz kellene, de amúgy érdekel is, mert a kötőjelest nem fogadja el szókozzel és anélkül sem. egyáltalán lehet ?
az érdekes az, hogy a harmadik beírásom a .r01-el az összes ilyen fájldarabkát kijelöli, azzal nem is kell semmit csinálni. viszont a betű nélküli számnál csak azt a számozott részt pipálja ki amennyi az értéke. azért nem fogok vagy százat beírni a sorba -
 #644
#644
Köszi. Akkor megveszem. -
Thibi #643 Régen olvastam,most belelapoztam: egyáltalán nem tömény matematika, olvasmányos matematika történeti áttekintés a sejtésről,illetve a vele összefüggő tételekről. -
 #642
#642
Srácok olvasta itt valaki Simon Singhtől az A nagy Fermat-sejtés című könyvet? Mennyire tömény matematika és mennyire regény? Akik olvasták, el tudnák mondani a véleményüket? -
 #641
#641
Én se értettem sose  ,de a legeccerübb megoldás ha olyan mellé ülsz aki érti...
,de a legeccerübb megoldás ha olyan mellé ülsz aki érti... ...
...
De ms-nak van egy tök jó sugója én is abból értettem meg(egyszer)...DE csak egyszer is volt rá szükségem. -
Dajin #640 ha valaki eltudná magyarázni az excelben azt a logikao függvényt hogy FKERES és hogy mire jó megköszönném.
addig tudom hogy egy tábla bal szélső oszlopában megkeres egy értéket és a metszéspontot adja eredményül.
nade mecsinálom hogy függvény beszurása és kijön hogy
keresési érték:
tábla:
oszlop-szám:
tartományban keres:
tehát csináltam bal oldalra növekvő sorrendben egy az A oszlopban egy számsorozatot, de tovább nemértem, mert amit feljebb beirtam hogy érték meg tábla, na ide nem teljesen vágom hogy mitkéne irni.. -
Realtibi #639 na ilyet még nemtanultunk
akkor majd jövöre biztos fogunk
meg majd lesz még faktom is -
 #638
#638
Igen, igen, kissé hamar gondoltam, hogy könnyedén megoldható, nem néztem a közös nevezőre hozást...! Azért örülök, hogy sikerült! Valóban a szorzatuk miatt kell az első azonosság! Gratula a megoldáshoz! :)
-=ZR=- -
 #637
#637
Mégis megoldható, de alkalmazni kell az
sin(2 * alpha) = 2 * sin(alpha) * cos(alpha)
valamint a
sin^2(alpha) + cos^2(alpha) = 1 azonosságokat
1.
sin(alpha) + cos(alpha) = p * sin(2*alpha) (p = 35/12)
2.
1 + sin(2*alpha) = p^2 * sin^2(2*alpha)
y = sin(2*alpha)-ra egy másodfokú egyenlet:
3.
p^2 * y^2 - y - 1 = 0
y1 = 0,96
y2 = -0,4898
Ezekből 2*alpha az asin fv-el visszakereshető, amiből a cos(alpha) kiszámolható,
aminek a reciproka az x.
Megj.: alpha értékeit vissza kell helyettesíteni az 1. egyenletbe, mert a négyzetre emelés miatt csak a megoldások fele lesz jó. -
 #636
#636
Szép észrevétel, de hogyan kerülöd el, hogy végül egy negyedfokú egyenletet ne kapjál? Ha beírod sin(alpha) = sqrt(1 - cos^2(alpha)), akkor ugyanott vagy, és cos(alpha)-ra kapsz egy remek 4-edfokú egyenletet. -
 #635
#635
Csak mellékesen jegyzem meg, nehogy valaki elkezdjen játszani itt ténylegesen a szögfüggvényekkel, mert látható, hogy x=1/cos(alfa), tehát csak cos(alfa)-ra kell megoldani, az hogy mennyi az alfa, senkit sem érdekel! A sin(alfa) helyére is be kell írni, hogy gyök(1-cos(alfa)^2). Bár, kinek mi tetszik...
-=ZR=- -
 #634
#634
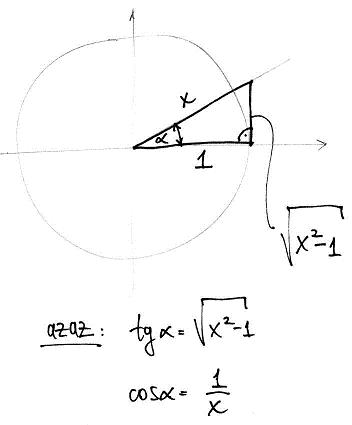
Hi All!
Az ilyeneknél illik gyanakodni azonnal szögfüggvényekre! Rajzolni kell ügyesen derékszögű háromszögeket és abból kifejezni a számlálót nevezőt sin, cos, tan és ctg függvényekkel!
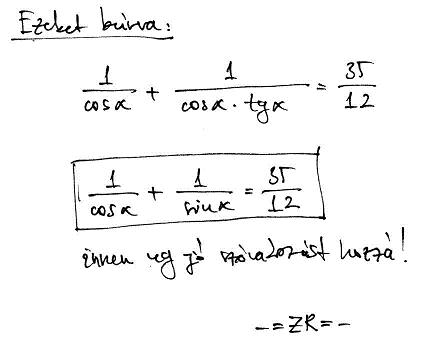
És azután beírva ezeket a számláló és nevező helyére, lehet játszani a trigonometrikus összefüggésekkel!
Ahogy írtam is: innentől jó szórakozást hozzá! :)
-=ZR=-
Ui.: szólni kéne a matekfaktos tanárnak, hogy ilyen példákat gyakoroltasson orrba-szájba, mert más szemléletet ad! Pl.: régi korok BASIC programozói tudják, hogy a számítógépeken volt sin, cos, tan és atan (arkusz-tangens) függvény, de nem volt asin és acos. Hát pont ezért. -
 #633
#633
Jaja ez volt. Matek specen vok ugyhogy ott előfordul az ilyesmi. -
 #632
#632
Remek, kiszedte a fórum a szóközöket.
A lényeg, hogy ez egy 4-edfokú egyenletre vezetne, középiskolában ez nem túl jellemző feladat. -
 #631
#631
Biztos, hogy ez volt?
X 35
X + ------------ = --
sqrt(X^2 - 1) 12
-
 #630
#630
annnyit segítek, h gyök(xnégyzet-1)=gyök(x+1)(x-1) -
 #629
#629
Üdv minednki! nekem is lenne egy feladatom matek dogába írtuk és nem vok benne biztos h jó lesz! A feladat: X+X/gyök(Xnégyzet-1)= 35/12
-
 #628
#628
Számtani sorozatnál az első 110 elem:
5, 5+1*3, 5+2*3, 5+3*3, ..., 5+108*3, 5+109*3
5+2*3 = 11 osztható 11-gyel, ezután már csak azok oszthatók, amelyekhez 11-gyel osztható számmal többek ennél. Mivel a 3 és a 11 legkisebb közös többszöröse a 33, így a 11-gyel osztható elemek:
5+2*3+0*33, 5+2*3+1*33, 5+2*3+2*33, 5+2*3+3*33, 5+2*3+4*33, ..., 5+2*3+(n-1)*33,
ahol n jelöli a 11-gyel osztható elemek számát
Mivel az első 110 elemig kell vizsgálódni:
5+2*3+(n-1)*33 <= 5+109*3 < 5+2*3+n*33
2*3+(11*n-11)*3 <= 109*3 < 2*3+11*n*3
2+11*n-11 <= 109 < 2+11*n
11*n-9 <= 109 < 11*n+2
11*n <= 118 < 11*n+11
n <= 118/11 < n+1
n = 10, mivel n egész szám, és erre teljesül a fenti két egyenlőtlenség.
Tehát ez az a 10 elem:
11, 44, 77, 110, 143, 176, 209, 242, 275, 308 -
 #627
#627
:)
Ez volt az A feladat, a B ugyanez csak számtani sorozattal! -
Realtibi #626 de azért kösz mindent
tök zsirra sikeredett a doga
4/4 feladat
remélem nem hibáztam el egy kér dolgot benne
és akkor lesz egy 5 ösöm -
Realtibi #625 közben rájöttem hogy a cos mért 2 pi -
 #624
#624
"2
2x+x=2pi+k2pi
na és itt mért can két pi???
periodus miatt vagy mért???"
Semmi gond nincs ezzel:
3x=2pi+k2pi
3x=(k+1)*2pi, új paraméter bevezetése: l = k+1
3x=l*2pi
x=l*2pi/3
"sin3x=sin meg cos3x=cos x"
sin(3*x)=sin(x)
1.
3*x = x + 2*k*Pi
2*x = 2*k*Pi
x = k*Pi
2.
3*x + x = Pi + 2*k*Pi
4*x = Pi + 2*k*Pi
x = Pi/4 + k*Pi/2
cos(3*x)=cos(x)
1.
3*x = x + 2*k*Pi
2*x = 2*k*Pi
x = k*Pi
2.
3*x + x = 2*Pi + 2*k*Pi
4*x = 2*Pi + 2*k*Pi
4*x = 2*(k+1)*Pi, új paraméter bevezetése: l = k+1
4*x = 2*l*Pi
x = l*Pi/2 -
 #623
#623
Mivel az 5, a 3 és a 11 is prímek, és a mértani sorozat első 110 eleme:
5, 5*3, 5*3^2, 5*3^3, ..., 5*3^108, 5*3^109 prímtényezős felbontásban, ezért semelyik elem nem osztható 11-gyel. Tehát a válasz: 0 a valószínűsége. -
 #622
#622
Van egy mértani sorozat, első eleme 5. Hányadosa 3. Mekkora annak a valószínűsége, hogy az első 110 elemből egyet kiválasztva az osztható lesz 11-el?
Emelt szintű matek érettségin volt! :) -
Realtibi #621 meg van egy fügvényes kérdésem is
2sin(x+pi/6)-1
ezt a fügvényt kéne elemezni ugy hogy nincs lerajzolva
tehát a zh min max értékeket csak számolással határozzuk meg
nálam az a pi/6 zavart be nagyon
ezt is elöre is kösz -
Realtibi #620 Meglett a föci meg is mondta már a tanár 5 ös lett
megint lenne kérdésem
sin2x=sinx
1,
2x=x+k2pi
x=k2pi
2,
2x+x=pi+k2pi
3x=pi+k2pi
x= pi/3+k2pi/3
a másik
cos2x=cosx
1
2x=x+k2pi
x=k2pi
2
2x+x=2pi+k2pi
na és itt mért can két pi???
periodus miatt vagy mért???
és ezeket lécci irja le valaki sin3x=sin meg cos3x=cos x ra
elöre is köszi -
Realtibi #619 de legalább megértettem
kösz
az elöbb nem volt tiszta mostmár az -
Realtibi #618 hát egyszer biztos fogod tanulni
aztán akkor ha nemérted jöhetsz ide:D -
Realtibi #617 jolvan azért nem kell megverni:D
-
Goth #616 és most komolyan, ez jó is valamire? :D Ebből szart nem értek, és őszintén szólva nem is szeretnék :D -
 #615
#615
Mi ez? Olvasd el, hogy mit írtál!
"(x-Pi/2)-(x-pi/2)"
Ez 0 lenne, és sin(x) + sin(0) miért lenne egyenlő 2*sin(Pi)-vel?!
De különben is:
cos(x-Pi/2) = cos(-x+Pi/2) = sin(x)
(felhasználva a cosinus fv párosságát, és az általad említett sin(L) = cos(90-L) azonosságot)
És így már ugyanaz jön ki, mint nekem a #612-ben: 2 * sin(x) -
Realtibi #614 hopp ez ma jutott eszembe
az azonosság igy szol hogy
sinL=cos (90-L)
tehát
sinx+cos(x-Pi/2)=sinx+sin [(x-Pi/2)-(x-pi/2)]=2sinpi
én erre gondolok de ha nem akkor
javitsatok ki ha tévednék
-
Realtibi #613 kösz
végülis én is ezekre az azonosságokra gondoltam
de nem volt kedvem megoldani meg ábrázolni
inkább föcit tanultam mert hétfön vizsga