4415
Matematika feladatok
-
xDJCx #892
Ezt is lehet addig egyszerűsíteni, amíg számológéppel nem számolható:
Tényezőnként átírva faktoriálisos alakra, majd egyszerűsítve :
90!/(3!*87!) * 10! /(2! * 8!) / (100! /(5! * 95!))=
88*89*90 /(1*2*3) * 9*10 / (1*2) / ((96*97*98*99*100)*(1*2*3*4*5)) =
= 88*89*90 /(1*2*3) * 9*10 / (1*2) * 1*2*3*4*5))/(96*97*98*99*100)=
= 88*89*90 * 45 * 4*5 / (96*97*98*99*100) =
88*89*90*45 / (95*97*98*99*5) = ez már számolható egyszerű számológéppel = 0,070219...
-
Gascan #891 Casio fx911W :) másod évfolyamos közgázos vagyok, nem hinném, hogy mi foglalkoztunk volna a Stiling formulával csak pl. volt egy olyan feladat a vizsgán, hogy (90 alatt 3)(10 alatt 2)/(100 alatt 5) és erre a tesztben megvolt határozva 4 érték, azokra sajnos már nem emlékszem :) -
#890
merthogy biztosan van rajta nPr és nCr feliratú billentyű, ami asszem kombinációt és variűciót számol, mégpedig ismétlés nélkülit. -
#889
és milyen típusú az a számológép??? -
#888
és mi a francnak 100!-t számolni??? Ha kombinációkat kell (n alatt a k), akkor is úgy kell elvégezni, h a nevezőben és a számlálóban levő szorzatokat le kell egyszerűsíteni:
(90 alatt 5) = 90!/(5!*85!) = 90*89*88*87*86/5!
így már számolható. De lehet használni - ha ténzleg kell ekkora permutációkat számolni - használni a Stirling formulát, mégpedig a ln(n!) közelítő számításának módját. Az nem baj, ha közelítő, ilyen nagyságrendnél lényegtelen a pontos érték - ha van 222 recepted és hánzféle sorrendben főzhetsz belőle, az már nem számít, hogy a 1.121*10^426 -ban mi van az ötödik jegy helyén... ;)
Egyébként ennek a logaritmusa 981.015, a Stiling formula pedig
ln(n!)~~(n+1/2)*ln(n)-n+ln(gyök(2*PI))=981.934 -et ad, ami n!~~2.808*10^426 és ez egész tűrhető. Persze, azon el kell gondolkodnod, h a e^981.934 -et hogy számolod, de ez nem okozhat gondot ;) !!! -
Gascan #887 heló, kedden lesz valószinűségszámitás vizsgám és be kell vallanom picit hátrányban vagyok mert nem mindegyik előadáson vettem aktivan részt.... megtudná nekem valaki mondani, hogyan lehet kiszámolni gyorsan 100! (faktorialist), kisebb faktoriálisokkal még tudok számolni de ekkora összeget még a speckós zsebszámológépemnek is meghaladja a képességeit????? van erre valami olajozotabb módszer?
-
#886
Jahh és itt a nagy kérdés:
Mi volt előbb a tyúk vagty a tojás...
-
della #885 Hát ez éppen olyan, minthogy az Ősrobbanás előtt nem volt semmi, vagyis inkább az abszolút semmi volt, de akkor miből lett az Ősrobbanás? 
-
#884
én vegyészként mindíg azon röhögtem, h elektrolízisnél szépen lerajzolták a vasatomokat, mellé meg az oldatot mint folytonos közeget.
engem is izgattak olyan kérdések, h mi van, ha kiszivattyúzom a közeget egy térből és marad a vákuum. de mi van akkor, ha a vákuumot is feltekerem, mint egy szőnyeget? mi marad akkor? -
#883
Nos minél többet tudsz, annál több dolgot nem :) Szóval szerintem érdemes belemenni ilyen "apróságokba" de nem minden esetben :) Én csak annak nézek utánna, ami érdekel. -
Bammy #882 Ez nem ide fog tartozni de lehet máshova nem néznek be azok az arcok akiktől véleményt várok:).
Nha ott kezdeném, hogy egy filmben, illetve sorozatban (prison break-a szökés) említették a következőt: van benne egy nagyon okos srác, és az ő pszihológusa mondta valakinek hogy az a srác olyan, hogy minden dolgot részletesebben akar meglátni, a legapróbb részleteibe belemenni, és ez a tulajdonság ha sok ésszel párosul akkor egy zsenit hoz létre, ha viszont kevéssel akkor elmebajokhoz vezethet". Na msot ez lehet marhaság, de engem azért fogott meg, mert olyan ember vok aki sokat gondolkozik ezen. Pl ilyenen hogy nemtom felfogni hogy ott egy vasdarab, és abban vannak ilyen kis szar elektronok meg protonok, neutronok, az elektronok kívül vannak, aztán van amikor leválnak, stb. nemtom elképzelni a kémia dolgokat, a kötések létrehozását, stb. Hogy ez hogy valósul meg..kémiában a telített szénhidrogéneknél az órán kb 5-ször felmordultam magamba hogy bazmeg, most ez mi, ez a sok szar, ez hogy van jelen egy széndarabban...Aztán kb 10 perces filózás után jövök rá, hogy nincs értelme az egésznek, és leszarom:) így van és kész....de azért kíváncsi vok hogy más is így van e, vagy leszarja és nem foglalkozik ilyenekkel:) -
#881
hááát, ha egy kis cégnél van egy pénzügyi vénával megáldott jó (gépész)mérnök, akkor nem kell egy közgázosnak fizetni az egyszerűbb pénzügyi döntésekhez. (Pl.: amortizációs, törlesztéses, raktárkészletes, optimális üzemvitel, -termelésnagyság, stb... feladatok megoldása. Amúgy is, egy mérnök jobban el tudja készíteni a probléma matematikai modelljét és meg is tudja oldani, ráadásul tudja is érthetően tálalni. Azért kell egy könyvelő, aki a cég és a dolgozók pénzügyi dolgait intézi, de közgazdász nem feltétlenül. Ráadásul lehet a mérnöki diploma mellé könyvelői vizsgát tenni...)
Anno, amikor elköltöztem a koliból, az időközben feleségemmé lett ;) barátnőmmel és kénytelenek voltunk hűtőszekrényt és mosógépet hitelre venni, akkor megkeresett minket a bank és tettek egy jó ajánlatot, mivel olyan rendszeresen és pontosan fizettük a részleteket.
Elmentünk, Jolánka - a habosra nyalt ügyeletes bankcica - elmondta, mi az ábra, majd adott 5 percet, amíg kettesben a feleségemmel átgondolhattuk a dolgot. Visszajött és szépen elmagyaráztuk neki, hol sántít a dolog, amin annyira meglepődött, hogy rögtön szólt Öltönyös Jankónak, akinek szintén el lett magyarázva a dolog. Csak pislogtak és elengedtek, hogy nem sikerült újabb hitelre rávenni bennünket - pedig akkor még csak egy fizetésből éltünk és jól jött volna egy kis zsé. -
Bammy #880 Most leírtad hogy mire jó a KÖZGAZ. De hogy miért kell ezt egy gépészmérnöknek tanulni azt még mindig nemtom:). Közgazdászból úgyis van elég nem? Fél ország oda jár ha jól tom. -
#879
...sőt, volt az életemnek olyan szakasza, amikor a Pareto-hatékonyságot is értettem... ;) -
#878
Közgáz: otthon kiszámoltam édesanyámnak, milyen tojást éri meg keltetni a keltetőgépében. ÁKFN, fedezeti pont, üzembezárási pont, állandó-, változó költségek, stb... Mindíg is szerettem...
Jah, eléggé mérnöki beállítottsággal vagyok megáldva. De elég hamar sikerült némi matekot felvonultatva belátni, h nem éri meg felvenni a diákhitelt. Lett is ebből egy diákhitelt számoló Excel tábla, mindenki okulására. -
#877
Mindkettő, de a teniszt csak nézem, bár sokszor erős ingerenciám van ezt is csinálni, de se pénzem se időm erre. -
#876
Eddig nem a röplabda volt a mániád? Már a tenisz is... :) -
#875
Majd holnap, de nem sok köszönet lesz benne, mert alig tanultam valamit. Túl jó meccsek vannak az Austral Openen. :) -
#874
Ha jól tudom már minden karon vannak közgazdasági tárgyak. És most elsüthetném azt a jó kis nagyképű poént hogy azért mert a mérnökök értenek a közgázhoz is, viszont a közgazdászok nem értenek a mérnöki dolgokhoz. (ez persze nem igaz) -
Bammy #873 Őőő én még nem 12.-es vok:). 10.-es vagyok csak van egy elképzelésem hogy gépészmérnökire szeretnék menni. Végülis csak a Miskolci egyetemen gondolkodtam vagy a BME-n. Viszont amit nem értek hogy ha vki gépészmérnöki kara jár akko mé kell közgazdaságtant tanulnia?:S
Amúgy persze minden kedves gépészmérnökhallgatótól várom hogy egy 10.-es gimisnek adjon jó tanácsokat:D. Pl. mi az ami nagyon szükséges hogy erősen vágjam, mi az ami kevésbé, stb stb. -
cleric #872 Köszönöm a segítséget! -
#871
Te meg miért nem vizsgázol? :D -
#870
Pontosan! -
#869
Ennyi a megoldás. -
cleric #868 Na vákicsit! A hatszöget 6 darab egyenlő oldalú háromszög alkotja? -
cleric #867 A gúla alapélét (tehát a hatszög egyik oldalát) és a gúla magasságát tudom. -
#866
És ha a hatszöget két (egyenlő oldalú) trapézra bontanád fel? (az a baj h nem tudom milyen adatok vannak megadva) -
cleric #865 Légyszi segítsetek ki gyorsan!
Szabályos sokszög (esetemben hatszög) alapú gúla alapéle és magassága adott. Felszín, térfogat a kérdés. Ehhez azonban kellene képlet:
- a hatszög területének kiszámításához
- a hatszöget alkotó kis háromszögek magasságának kiszámításához
Innen már menne. Tudom, középiskolás anyag, de egyszerűen nem emlékszem :) Köszi! -
#864
Az ábrázoló geometria az ami egy gimnazista számára elég hardcore. Nekem elsőre nem is sikerült.
Arra viszont készülj fel, hogy sajna a BME-n az első félévben 4x45 KÖZGÁZ órád lesz. Agyrém. Nekünk 2x45 volt, de attól is a falat kapartuk kínunkban. -
#863
Én hatodéves gépesz vagyok a BME-n és közlöm, hogy nem kell izgulnod a Gépészeti alapismeretek tárgy miatt, legalábbis, ha BME-re mész gépésznek. Nekem még Általános géptan név alatt futott 5 éve, de a lényege annyi, hogy alig durvább, mint egy erősebb gimnáziumi fizka, de abből is csak az alap mechanika és hidrosztatika. Hőtan rész nincs is.
Alapvetően arról szól a tárgy, hogy megtanítják azt rendssen amit meg kell(ett) volna gimnáziumban és lesz néhány mérés is, ahol a gyakorlatban táthatjátok ezek hasznosságát.
BME-re mész? Mert tudok adni tippeket. ;) -
Bammy #862 Igen gépészeti alapismeretekből az érettségizett aki gépész suliba járt előtte is! Kár mert én szívesen tanulnám..:( -
ugot2know #861 hopp,csak nem Nyíregyre jársz? -
Thibi #860 Gondolom gépészeti alapismeretekből az érettségizett,aki valami gépipari szakközépiskolába járt és fő szaktárgya volt -
#859
Én még a "régi" érettségi rendszerben a matek és fizika felvételimet számíttattam be érettséginek. Tehát elmentem felvételizni a BME-re és az ott írt felvételi alapján kaptam érettségi jegyet. Idén végzek a BME gépész kar energetika szakán. -
Bammy #858 Igazad van, bár azért valamennyire a jegyek is tükrözik a dolgoka,t és a tananyag végülis mindenhol ugyanaz, csak valahol megvan a lehetőséged magolással jó jegyet szerezni és kijavítani a szart, vhol nincs. Pl a mi tanárunk oylan hogy egyszer egy lány bemagolt mindent azt egyest adott neki azzal az indokkal h ő ezt nem érti csak magolt. Nha de nem ez a lényeg, értem a 2 tárgyat, lényegében ez a gépészeti alapismeretek dolog érdekelt volna....Justin te miből érettségiztél+hova jársz? -
#857
Érettségi részhez nem tudok hozzászólni érdemben.
A matek meg fizikánál meg nem az a lényeg hogy hányas vagy (hiszen egy könnyebb suliban könnyebb jó jegyeket szerezni) hanem hogy érted-e ezt a két tárgyat. Fizikából főleg a mechanika részre kéne figyelni. (nem tudom ezt most milyen részletességgel tanítják). A fakt midnenképp hasznos.
Rajzolni majd megtanítanak, esetleg a térlátás fejlesztésével tudod magad előkészíteni a gépelemek nevezetű szépséges tantárgysorozatra. Ja és matek geometriát se hanyagold :) -
Bammy #856 Csáttok! Láttam itt jópár gépészmérnököt szóval őket szeretném kérdezni. Én is gépészmérnökire akarok menni, 10.-es vagyok most. Hogy a tanulmányi eredményem említsem, átlagosan 4-es vagyok, nyelvekből vagyok jó, fizikából vok 5-ös, és fizika faktra szeretnék majd járni. Matek megy, sokan mondták hogy jó érzékem van hozzá, de csak a 4-es sikerül mindig, nha mindegy:(. Szal a legfőbb kérdésem hogy van egy ismerősöm aki gépészmérnökire jár és azt mondta hogy ő gépészeti alapismeretekből érettségizett:s na most gondolom ez egy előnyös dolog úgyhogy nekem is kéne ilyen! De ez hogy van? A sulikban van általában ilyen képzés? mert én ilyenről még nem hallottam..mondjuk akkor nem fizikából érettségiznék. Jha és még valami...rajzolni nem nagyon tudok, de úgy hallottam hogy az is nagyon kell:SSS Hát 10.-es vok szal lehet későn, de elkezdem fejleszteni a rajztudoásom, remélem lesz valami. -
Bammy #855 Köszi! Nagyon kössz tényleg! bárcsak én is így a kisujjamból ráznám ki ezeket :( -
xDJCx #854
Négyzetre emeljük az egyenlet mindkét oldalát, majd átrendezzük, hogy az egyik oldalon legyen gyök(4+x), majd ezt az egyenletet is négyzetre emeljük, az így kapott egyenlet nullára rendezve egy másdofokú egyenletet kapunk, ennek gyökei pl. a megodlóképlettel x=21 és 32. Behelyettesítve ezeket az eredeti egyenletbe csak a 21 igazi gyök. Tehát x=21.
![]()
[/IMG]
-
xDJCx #853
2.)
Legyen h az órák száma, n az egy óra alatt legépelt oldalak száma.
Ekkor felírható az akábbi két egyenlet:
n*h = 120 első egyenlet és
(n+2)*(h-2) = 120 második egyenlet.
A második egyenletben elvégezve a műveleteket:
n*h+2*h-2*n-4=120
Ide az n*h helyére behelyettesítve a 120-at az első egyenletből, majd mindkét oldalból kivonva 120-at, majd 2-vel osztva a két oldalt kapjuk:
h-n=2, ebből h=2+n,
ezt behelyettesítve az első egyenletbe: azaz n*(2+n)=120 kapjuk a
n*n+2*n-120=0 másdofokú egyenletet, ennek megoldásai: n= 10 és -12, ebből pozitív értéknek van értelme, azaz n=10, és a h=2+n, ebből h=12.
Azaz 12 óra alatt gépelte le.
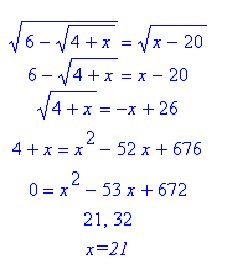[/IMG]