4415
Matematika feladatok
-
xDJCx #972 másodikra az egyenletek:
legyen egységnyi a medence térfogata,legyenek a töltés vagy lefolyás sebességei rendre M, H, L (meleg, hideg, lefolyó), ekkor: M*60*8 = 1-ből: M=1/480 (percben mérve az időt)
H*60*10=1 -> H=1/600, 6*60*L=1 -ből L=1/360
legyen t a 7h30-tól eltelt idő a medence megtöltéséig percekben:
M*t+H*(t-45)-L*(t-90)=1, ahol csak t ismeretlen
stb... -
 #971
#971
Köcce!
A másodikra is van? -
xDJCx #970 elsőre:
a szám xy azaz 10*x+y:
1) x+y =9
2) 10*x+y - 10*y-x=45
2)-ből x-y=5 -> x=5+y
1)-be helyettesítve: 5+2*y=9 -> y=2, x=7
ellenőrzés 72-27=45 ,7+2=9
-
 #969
#969
Légyszi erre egy megoldást ha tudtok mi hamarabb legjobb lenne 2 órán belül :)
2 feladat is van (légyszi az egyenletet írjátok le)
Egy kétjegyű szám jegyeinek a összege 9. Ha a szám értékeiből kivonom a jegyei felcserélésével nyert kétjyegyű számot, akkor 45-öt kapunk. Mi az eredeti kétjegyű szám?
A melegvizes csap egyedül 8 óra alatt tölti meg az üres medencét. A hideg vizes csap egyedül 10 óra alatt tölti meg az üres medencét. A leeresztő csap egyedül 6 óra alatt ereszti le a teli medencét.
Mikorra telik meg az üres medence, Ha 7:30-kot kinyitják a meleg csapot, 8:15-kor a hideget, és 9:00-kor a leeresztő csapot???
LÉGYSZIVES MIHAMARABB, NAGYON SÜRGŐS
THX -
Mirk #968 vagy írd ki hogy alfa:) -
 #967
#967
Arra azért figyelj, hogy az alfa latin betűs átírása "a", mivel ezt a hangot jelenti a görögben, az az L betű maximum a csúnya kézírású matektanároktól jöhet ;) -
 #966
#966
igazad van,gyorsan akartam írni a megoldást,és nem gondolkoztam:) -
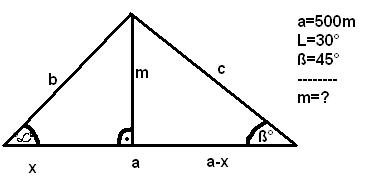
dXter #965 kicsit egyszerűbb megoldásnak tűnik, hogyha meg is nézed az ábrát...
ha lerajzolod magadnak normálisan, akkor látszik is, hogy amit te 'a-x'-szel jelöltél, az =m, mivel egy egyenlőszárú derékszögű 3szögről van szó.
a másik kisebb 3szög pedig egy félbevágott szabályos 3szög, aminek a magassága, azaz az ábrán 'x', gyökháromperkétszerese a szabályos háromszög oldalának. ezért x=gyök3/2*2m=gyök3*m(=3·0,5*m)
így már csak egy ismeretlened van, és egy egyenleted:
500=m+gyök3*m, ahonnan m=183,0127...stb.
//és így könnyebb kiszámolni a b és c oldalt is: b=2m, mert a szabályos 3szögnek ekkora az oldala, c=gyök2*m, mert az meg egy félbevágott négyzet, és 'c' pont az átlója lesz.
-
 #964
#964
955:
1.m / a-x = tg ß
2.m / x = tg L
2 ismeretlenes elsőfokú egyenlet,innen már remélem te is tudod. -
 #963
#963
akkor szinusz tétellel meg lehet tudni a többi oldalt. -
Mirk #962 az alfa akar lenni sztem -
 #961
#961
ja hogy 45fok az nem derékszög 
-
 #960
#960
és mi az "L"?.... -
 #959
#959
xar a rajzod, mert a béta derékszögű... -
Bammy #958 Hello!
Nha mivel itt olyan sok a mérnök lenne egy kérdésem. Vagy gépész vagy villamosmérnöki egyetemre szeretnék menni, nemtudom melyikre mennék többel de szerintem ezt senki nem tudja megmondani :/. Viszont az lenne a kérdésem hogy, ugye matek meg fizikát kell ehhez kőkeményen vágnom :) Ami meg is van de matek meg fizika mely részeit kell pl egy gépésznek vágni, és melyiket egy villamosmérnöknek?
Egy ismerős mondta hogy pl gépészmérnökin mechanikát kell vágni nagyon, meg geometriát..persze ez nem azt jelenti hogy mást nem csak gondolom az nem jó ha pont ezekből vagy gyengébb. -
Mirk #957 valószínűségszámítás könnyű:) -
 #956
#956
Olvass -
 #955
#955
ebben segítenétek? az jólenne ha levezetnétek a képletet:D -
 #954
#954
Hy.A valószínüség számítás nehéz lessz mert most fogjuk venni és félek hogy megbukok. -
 #953
#953
Aham, akkor minket félreinformáltak, hogy ez az R^2 a korrelációs együttható négyzete akar lenni... Na, erre én is ránézek alaposabban, de köszönöm az utánajárást! Persze mielőtt kinyitottam a számat, én is megleshettem volna, hogy ez az "R" nem az az "r". -
xDJCx #952 Az excel által ebben az esetben az r2-re számolt -2,6 ki is jön a súgóban megadott képlet alapján: R2= 1 - SSE/SST, ahol
SSE = szumma(Yi - Ykozi)^2
SST= szumma(yi^2)- szumma(yi)^2/n,
yi az eredeti egyenes i-edik y koordinátája (y=-x+3), ykozi a kozelitett egyenes i-edik értéke (y=0,8x), egyenesnek..., n a figyelembe vett pontok száma itt ketto , a szumázás erre két pontra megy konkrétan:y1=2, y2=1, ykoz1=0,8, ykoz2=1,6
SSE= (2-0,8)^2+(1-1,6)^2 = 1,8
SST= (4+1)-((1+2)^2)/2 = 0,5
R2= 1-1,8/0,5 = -2,6
-
xDJCx #951 Furcsa eredmény egy négyzettől, de nem is a szokásos szemléletű görbeillesztést kérsz az exceltől ( origóra illeszkedjen az egyenes, a két pont pedig nem origóra illeszkedő egyenest ad meg eleve, persze lehet így is értelme a dolognak...) Nem feltétlenül bug, mert az R2 értelmezése a súgó szerint: R2 = 1- SSE/SST, ahol SSE az eredeti és közelítő görbe közti négyzetes eltérést jellemzi, SST az eredeti görbe értékeinek szórásnégyzete vagy ilyesmi, ha jól látom a súgóban. Ha nagy a különbség a két görbe között, ami most teljesül, lehet 1-nél nagyobb a hányados! Általában görbeillesztésnél egy görbéhez alegjobban illeszkedő egyszerűbb görbét szoktuk keresni, és ezt jellemzi az R2, ez pedig más helyzet. -
 #950
#950
nem bag, fícsör! -
 #949
#949
Hőn szeretett MS Excel bugos:
Tessék origón átmenő egyenest illeszteni az alábbi (x,y) formában adott adatsorra: (1,2) és (2,1). A meredekség az OK, de a determinációs együttható R^2=-2.6, ami két okból is elgondolkodtató: egyrészt nem esik 0 és 1 közé, másrészt negatív (ha van köze bármilyen "négyzet"-hez, ez felettébb erősen elcseszettnek tűnik...)
Kommentek, ötletek??? -
della #948 Végigolvastam mégegyszer, és most már minden világos:D
köszi -
 #947
#947
hol nem érted? -
della #946 Nekem is a 2, 5, 8, 11 sorozat jött ki végül, de csak úgy, hogy próbálgattam behelyettesíteni, csak azzal az a baj h nem zárja ki hogy van másik megoldás is. Mi órán úgy csináltuk, hogy mivel páros tagú a sorozat, ezért a2 és a3 között vettünk egy x-et és felírtuk úgy hogy a1= x-3/2d; a2= x-1/2d, a3=x+1/2d; a4=x+3/2d. így kijön egy másodfokúra visszavezethető negyedfokú egyenlet, és megkapjuk a d-t, és utána megoldásnak tényleg a 2, 5, 8, 11 sorozat jön ki 
köszi a segítséget
kz, a megoldásod tetszik, de még dolgozok a megértésén
-
 #945
#945
ó basszus aszittem ez egy másik feladat, nem a megoldás.
minek görcsöltem ennyit... ehh! -
 #944
#944
szorzatuk 880.
mi is a primtényezős felbontása?
880 2
440 2
220 2
110 2
55 5
11 1
az összegük 26, pozitív egészek, tehát minden szám 1 és 26 közé esik, sőtt.
mivel viszonylag kis számokról van szó, égyrészt fel lehetne írni az összeset, másrészt lehet próbálkozni is.
vagy tovább gondolkodni.
én ezt teszem most.
a 11-et 5-el nem lehet szorozni, csak 2-vel, (maximum egyszer, mert különben 26 fölé megyünk) az 22.
tudunk nagyobb számot kreálni 26 alatt?
nem.
akkor tegyük fel, hogy a 22 tagja (méghozzá a legnagyobb tagja) a sorozatnak. a maradék: 2,2,2,5. ezekből kell 3 számot csinálni.
a lehetőségek:
2,2*2,5. azaz 2,4,5,22, ami nem számtani sorozat.
2,2,2*5. nem jó. több nincs. tehát nem sikerült olyan sorozatot csinálni, aminek a 22 a tagja.
akkor mi a következő generálható szám? a 20 (5*2*2).
ekkor marad 2, 2, 11. ekkor a sorozat tagjai: 2, 2, 11, 20. ez nem számtani, tehát a 20 nem tagja a sorozatnak.
a következő? 2*2*2*2=16. marad az 5, ami nem három tag.
mi lehet még? (16 alatt.) a 11. akkor marad 2,2,2,2,5. ebből kell 3 szám (11 alatt).
pl 2, 5, 2*2*2, azaz 2,5,8,11. ez pl jónak tünik, mert számtani. az összeg? 26. akkor ez jó!!!
van más 2,2,2,2,5-ből? igen: 2,4,10, ami nem jó.
más ugyanezekből (még mindig 11 alatt?) nincs.
tovább nem kell mennünk lefelé, mert akkor a 11 kimarad. (mivel primszám, pozitív egészek szorzataként csak egyféleképpen (1*11) írható fel.)
...
hoppácska. az egyről megfeletkeztünk!!!
mármint az 1, mint a sorozat eleme szóbajöhet, mert a primtényezős felbontásban benne van és bár a szorzatot nem módosítja, az összeget igen, tehát a lehetőségét meg kell vizsgálnunk.
akkor nézzük tovább...
az előbb feltettük, hogy az egy nem tagja a sorozatnak.
de ha mégis, akkor tegyük fel, hogy tagja.
ekkor a másik két páratlan primtényező (5 és 11) közül az egyik köteles megszorozva lenni egy páros számmal.
ugyanis három páratlan szám összege páratlan,
két páros meg egy páratlan, az páratlan,
két páratlan meg egy páros, az pedig páros. nekünk ez utóbbi kell, mivel az 1 az páratlan, tehát még pontosan egy páratlan kell mellé, hogy az összeg páros (26) legyen.
tehát az 1 mellett, vagy a 11, vagy az 5 szerepel a sorozatban.
tegyük fel, hogy az 1 és az 5 szerepel. ekkor mivel 11-ből párosat kell csinálni, ezért megszorozzuk 2-vel. ekkor 1,5,8,22 összege nem 26. (2*2=4-el megszorozva túl vagyunk a 26-on)
akkor tegyük fel, hogy az egy és a 11 szerepel.
ekkor az 5-öt legalább egyszer meg kell szorozni 2-vel, tehát vagy a 10, vagy a 20 szerepel a sorozat tagjai között.
a 20 nem szerepelhet, mert 20+11+1 már rég több mint 26.
akkor szerepelhet az 1, a 10. a 11 ésmég?
maradt tehát 2,2,2, miből egy számot kell csinálnunk. eze a 2*2*2=8.
így a sorozat az 1,8,10,11 lenne, ami nem nyerő.
mivel (azt)hiszem, hogy minden lehetőséget végigvettünk, így kijelentem, hogy a sorozat tagjai csakis a 2, 5, 8, 11 lehetnek.
vagy elqrt@m valahol? -
Thibi #943 Egy számtani sorozat a,a+b,a+2b,a+3b alakú. A négy elem összege 4a+6b
4a+6b=26
2a+3b=13
pozitív egész számok körében erre két megoldás van a=5,b=1 és a=2,b=3
már csak azt kell megnézni,hogy melyik esetben lesz a szorzatuk 880 -
della #942 lenne egy feladatom:
Négy pozitív egész szám egy számtani sorozat egymást követő négy eleme. Határozzuk meg a négy számot, ha összegük 26, szorzatuk 880.
Várom az ötleteket, mert én eddig még nem sokra jutottam vele.
köszi :D -
 #941
#941
Ez is jó, isn't it?
(36@10)/(6@10)-(10@3) = (10@3)
azaz
36/6-3 = 3
Itt szám@számrendszer jelölést használok. -
stupido #940 itt egy feladat: 36__6__10 = 10 a számsor helyessé tételéhez használható +,-,*,/ és zárójel egyaránt. Kérem a megoldásokat!
Üdv
Kri
-
 #939
#939
húúú...
most ugrott be, csak télleg nincs időm!!!
nézzük a bal felső e1 egyenest. tutira benne van. keressük meg a b2-höz tartozó egyenessel való metszéspontját (legyen x és y ). aki e pont magassága alatt indul és érkezik (a(i) és b(i) is kissebb) az kiejthető.
most (rekurzívan) elosztjuk két részre a sikátort és külön kölön vizsgáljuk.
mad újra felosztjuk és újra...
több időm télleg nincs, remélem gondolatébresztőnek jó voltam! -
 #938
#938
hát igen, ettől féltem.
de szerintem csupán a végpontokból is megmondható, hogy 3, vagy kettő vesz-e részt az alkotásban.
ja, hoigy hogy???
hátőőőő...
most nincs elég időm.
de mi lenne, ha arányosítanánk.
tehát nem az a(j)-a(i) és a b(i)-b(k) távolságokat hasonlítanánk össze, hanem pl az (a(j)-a(i))/(a(j)-a(k)) és a (b(i)-b(k))/b(k)-b(j) arányokat.
vagy valami hasonlót...
szerintem a metszéspontok meghatározásával az a gond, hogy a triviális megoldásnál pl n=101 egyenes esetén (ami nem is sok) n!, vagyis 1*2*3*4*5*6*...*98*99*100 a metszéspontok száma. -
7evenb #937 Végig böngésztem a tiédet is, de h jól értem te is végig számolod az egyes metszéspontok helyét, és azokon lépkedsz végig a legmagasabbtól kezdve. Az eljárás jó, frappáns, de nem az igazi:), persze jobbat mutatni én sem tudok, de még agyalok rajta a hétvégén. -
7evenb #936
ha jól értelmeztem a 2.-est akkor a fenti ábra egy ellenpélda rá.
látható, hogy
a(j)-a(i)>=b(k)-b(i) és a(i)-a(k)<=b(i)-b(j)
is teljesül, de mégis felette van az e(i).
Az 1.-es szükséges, de nem elégséges.
Tehát félig meddig jó a megoldás, de nem teljesen.
Ezért gondoltam hogy először a 3 egyenesre adunk egy megoldást ami könnyen álltalánosítható. (és akkor nem kell ennyire elbonyolódni:)
Én arra gondoltam, hogy a párhuzamos szelők tételét lehet alkalmazni, vizsont az már ugyanannyi számítás mintha megadnám a pont helyét, pontosabban, az megadja a metszépont helyét, tehát az sem igazábol jó.
Másképp viszont aligha megoldható a dolog...legalábbis eddigi meglátásom szerint.
De a kérdés továbbra is nyitott.
ui.: konvex burok keresés = meghatározzuk az összes pontot, majd ezek közül megadjuk az extrémumok halmazát , vagyis a párhuzamos szelők tételét egyszerűbb alkalmazni. -
 #935
#935
meg ez is ott van:
"Konvex burok fogalma. Sikbeli konvex burok keresese:
egyenkenti hozzavetellel O(n log n) idoben;
,,csomagkotozo" algoritmussal O(kn) idoben;
,,oszd meg es uralkodj" modszerrel O(n log n) idoben."
-
 #934
#934
googl-ben leltem itt:
Terbeli konvex burok keresesere is van O(n log n) ideju algoritmus.
Mese: ,,oszd meg es uralkodj"; ezen belul ,,3D ,,csomagkotozes".
-
 #933
#933
akkor fogalmazzuk meg a problémát!
szóval van n darab egyenes, az a kérdés, hogy az egységsikátorban mely egyenesek vesznek részt a felső burkológörbe kialakításában.
az egyeneseket az egységsikátorba eső szakaszaik sikátorfallal való metszéspontjaival jellemezzük.
konkrétan legyen a bal legfelső metszéspont az a1, alatta a2, a3, stb...
legyen az a1-hez tartozó egyenes az e1, az a2-höz az e2, az a3-hoz az e3, stb.
tekintsük a sikátor falait y irányúnak, így a magasságok (a(i) és b(i) tulajdonképpen y koordináták)
legyen az e1 egyenes másik végpontja a b1, az e2-é a b2, az e3-é b3, stb...
az egyenesek egymással való metszéspontjait kiszámítani nem ér.
ha egy e(i) egyenes része a burkolónak, akkor f(i):=1, ha nem, akkor f(i):=0
úgy kezdeném, hogy minden f(i) értékét -1 re állítanék, hogy tudjam, róla még nem dőlt el, alkot-e, vagy se. for ciklusban értékadás
aztán az e egyenesek halmazából kivenném azokat, akik tutira nem alkotják.
mégpedig az alábbi két algoritmust alkalmazva:
1: távolítsuk el a halmazból azokat, akik az egységsikátoron belül végig egy másik egyenes alatt (pontosabban végig nem felette) haladnak.
ezek konkrétan azok, akikre igaz, hogy b(i)>=b(j) és i<j.
for ciklusban(1-től, i-re, n-ig) for ciklus (i-től, j-re, n-ig), bennük feltételvizsgálat, ha igaz, akkor értékadás f(j):=0
2: távolítsuk el azokat, akik valamelyik másik két egyenes burkológörbéje alatt (pontosabban végig nem felette) futnak a sikátorban.
legyen a vizsgálandó egyenes e(i), a másik kettő e(j) és e(k),
ahol j<k (vagyis a a(j)>a(k), azaz a bal oldalon e(j) magasabban van mint e(k))
és b(k)>b(j) (vagyis a jobb oldalon e(k) van magasabban mint e(j))
(így e(j) és e(k) már metszik egymást)
és j<=i<=k (vagyis a(j)<a(i)<a(k), azaz a bal oldalon e(i) e(j) alatt, de e(k)f elett van)
és b(j)<=b(i)<=b(k) (vagyis a jobb oldalon e(k) és e(j) közé esik e(i).
ekkor tehát a 3 egyene 3 pontban metszi egymást, de még el kell döntenünk, hogy a vizsgált e(i) a másik kettő burkológörbéje alatt fut-e végig.
ez akkor* van, ha
a(j)-a(i)>=b(k)-b(i).
tehát ha a fenti feltételek igazak, akkor a vizsgált egyenes is kiejthető.
három egymásba ágyazott forciklus belül feltételvizsgálat, ha igaz, akkor értékadás f(i)=0
a két algoritmusocskát (szubrutint) alkalmazva előbb utóbb minden egyenesnél f(i)=1, vagy f(i)=0 lesz, és akkor készen vagyunk.
azt hogy a két szubrutint felváltva, vagy az egyiket (konkrétan a másodikat) gyakrabban alkalmazva kell-e eljárni, vagy hogy az elsőt esetleg elég egyszer lefuttatni, azt nem tudom.
de a két algoritmus összevonható eggyé, csak az az érzésem, hogy nagyob ortó költségű lesz.
ha már költség, akkor nyilván jó lenne a egy többszörösen láncolt lista is, melyben csak a még nem kizárt egyeneseket tartjuk a(i) és b(i)szerint is láncolva, de erre már télleg nincs időm!
*ebbe csak azért nem vagyok biztos, mert nem bizonyítottuk azóta se
lehet hogy kéne még oda az "és a(i)-a(k)<=b(i)-b(j)" ... egyre bizonytalanabb vagyok... lehet, hogy a meredekségük (a(i)-b(i)) és az bal metszéspontok alapján burkoltan kiszámítva a metszéspontot jobban járnánk, mert nem kell konkrétan a metszéspont, csak az, hogy fölötte van-e a ... na mindegy.
amit leírtam nem olvastam át, úgyhogy elgépelés, vagy logikai bukfenc sem kizárt!!!