Matematika feladatok
-
 #747
#747
Tehát az elejétől:
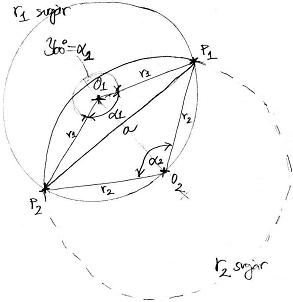
A kecske, aki jobb lenne ha birka lenne, az r2 sugarú körön tud mozogni, aminek a középpontja O2 és ez a pont rajta fekszik az r1 sugarú O1 középpontú rét kerületén:
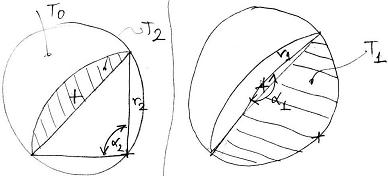
Ha jobban megvizslatjuk az első ábrát, az 'a' hosszúságú szakasz éppen 2 körszeletet metsz ki a két kör közös részéből - azt két körszeletre osztja, pontosabban:
Azt kell még itt észrevenni, hogy a két középpontnál jelölt alfa1 és alfa2 szögek között fennáll az alábbi kapcsolat:
merthogy kerületi és középponti szögekről van szó.
Namost egy körszelet területe számolható úgy, hogy:
és a másik pedig:
A fenti két egyenletet összeadva szépen kapunk egy területet, amit leosztva a rét területével (r1^2*PI) a kapott egyenletet 1/2-del egyenlővé téve meg kell oldani r2/r1-re.
Ami nem is olyan trivi.
Meg nehéz is.
Még ha áttérünk radiánra és a PI*alfa/180 tagok helyére mindenütt beírhatjuk azt, hogy alfa, mert ez csak erre volt jó (a Bronstejn szereti a fokokat, valszeg).
Én azt a módszert választottam, hogy előszedtem az egyik - a felvételinél használt és igencsak kedvelt - zsebszámológépemet és kihasználva, hogy van rajta SOLVER, megírtam neki a területarányt számoló algoritmust egy kis programba és asszontam, hogy na, ezt oldjuk meg a két sugár arányára.
A számológép így fest:
A rövidke program pedig:
LBL K
RCL K ; k itt r2/r1-et jelöli
2 ;
/ ;
ASIN ;
2 ;
* ; alfa1 számítása: alfa1=2*arcsin(k/2)
STO A
2
/
+/-
PI
+ ; alfa2
STO B
RCL A
ENTER
SIN
-
2
/ ; T1 számítása
RCL B
ENTER
SIN
-
2
/
RCL K
X^2
* ; T2 számítása
+ ; T1+T2 számítása
PI
/ ; (T1+T2)/T_rét számítása (T_rét=PI, egységsugarú!)
2
1/X
- ; itt pedig levonjuk az 1/2-et, hogy F(r2/r1)=0 alakú legyen az egyenlet!
RTN
54.0 BYTE
CK=EC52
A használata pedig:
FN= K
1 STO K
2
SOLVE K
eredményképpen pedig a már említett r2/r1=K=1.2212 értéket kapjuk.
Fontos, hogy a számoló RAD módban legyen!
-=ZR=-