4415
Matematika feladatok
-
#1372
akkor ezen (#1316) bizonyíthatsz! -
#1371
Elhiszed, hogy akármilyen számmal kapcsolatos dologból kihozok neked bármilyen teóriát? -
#1370
tehát pontosan mire vagy kíváncsi?
hogy ha a kezedben van két ász akkor mekkora a valószínűsége, hogy nyersz?
vagy lent van már a flop is?
vagy a turn is?
esetleg a river is?
-
pista007 #1369 Ja, úgy úgy... de taxas holdemben nincsenek jokerek ezért 52 lapos a pakli, amivel játszanak. -
#1368
"francia" kártya? mert az 52 lapos + 2 piros és 1 fekete Joker!
------
Amúgy érdemes kicsit megvizslatni a francia kártyát alaposabban:
52 lapos - egy évben 52 hét van
4 színt (pikk, kőr, treff, káró) tartalmaz - 4 évszak
4 x 3 = 12 figurája van (4 szín, mindegyikből bubi, dáma és király) - egy évben 12 hónap
színenként a lapok értéke 91 ( = 1(ász) + 2 + 3 + ... + 8 + 9 + 10 + 11(bubi) + 12(dáma) + 13(király) ) - egy évszakban levő napok száma, azaz...
az összes lap értéke 364 = 4 x 91, ami a napok száma egy évben (figyelembe véve a Jokereket, talán ezek szolgáltak pótnapként)
...és az ebben a jó, h erre én jöttem rá a nagy zsugapartik közben :P -
pista007 #1367 asszem 52 egy pakli, abból lejön a 2 joker, minden játékosnak 2 lap van a kezében, és először 3 lapot terítenek le, amit mindenki a saját kartyáival együtt felhasználhat, majd aehhez a 3hoz jön még 2.
A kártyák számának utánanézek még... -
#1366
hány meglévő kártyából? -
#1365
szóval, egyszerű ráérzéses próbálkozásra már nem is méltatod a feladatot? -
#1364
nekem van, de még váratok magamra kicsit! :))) de tényleg! nagyon egyszerű az ok: én erre írtam programot és nem találom a forráskódot! Elég régen volt, egy csokiszelet méretű CASIO zsebszámítógépre írtam BASIC-ben és semmire nem emlékszem belőle - másrészt ha írnál egy privátot a főnökömnek, hogy nekem most ezen kell dolgoznom ;) , akkor hamarabb meg is lenne. A kéziratom be van valahol dobozolva és nehezen hozzáférhető, tekintve, h az 1990-es évek végén követtem el :((( -
pista007 #1363 engem csak az érdekelne, hogy számítják ki azt, a meglévő kártyákból, h mekkora az esélyük a nyerésre, -
#1362
most is ezen dolgozom.
de ugye nem gondolod, hogy elárulom a nagy titkot?! -
7evenb #1361 meg akarsz gazdagodni:)
a játékelmélet azért kicsit messzebb mutat mint hogy ide elférjen...
-
pista007 #1360 valaki járatos a játékelméletben? pókerrel kapcsolatos esélylatolgatás, és a lapszámlálás érdekelne(texas hold'em) -
#1359
én még csak az elsőre sem jöttem rá :) -
#1358
a #1316-ra továbbra sincs senkinek ötlete? -
Rolcsi23 #1357 Sziasztok az alábbi feladat megoldásának lépéseibe tud valaki segíteni?
a rolcsi23@freemail-re adhatna ötleteket nekem(régen tanultam)[IMG]![]()
[/IMG]
-
Rolcsi23 #1356 Sziasztok az alábbi feladat megoldásának lépéseibe tud valaki segíteni?
a rolcsi23@freemail-re adhatna ötleteket nekem(régen tanultam) -
#1355
szép,
én a ((a*(a+3)+1)^2 heylett
a^4+6a^3+11a^2+6a+1 ezt vittem tovább, szimetrikus együtthatók vannak benne, az emberknek kedve támad leosztani a^2-el,
és kicsit átrendezgetve kijön hogy ez ((a+1/a)+3)^2 -
Thibi #1354 A 3.:
1*2*3*4 esetén 5, 2*3*4*5 esetén 11, 6*7*8*9 esetén 55 a keresett szám,ránézésre az első és utolsó szám szorzata plusz egy-nek felel meg a keresett szám. Csak ellenőrizni kell,hogy az a*(a+1)*(a+2)*(a+3)+1 és az ((a*(a+3))+1)^2 egyenlő-e. Mindkettőre a^4+6a^3+11a^2+6a+1 jön ki -
#1353
1) ne félj elnevezni a 2 átlót 4 ismeretlennel. fölirogatsz pár pitagoraszt, 4egyenlettel 5 ismeretlnnel, ügyeskedve marad 1 ismeretlen ;)
2) hát szierntem, mivel végtelen hosszú eza számsorozat, és 537 pl ösztható 3-al -> öszetett szám, és ha elé rakunk még 3db 5-öst, akkor is osztható lesz, minden 3dik szám, végtelen/3 = végtelen
3) ird föl n*(n+1)*(n+2)*(n+3) alakba, elvégzed, osztom, szorzom, kivonom, négyzetreemelem, gyökötvonok, elszotom gyökPI-vel, kifejezem, befejezem. tehát, ügyeskedve ki fog jönni :)
Nem veszem töled el azt az örömet hogy végigküzd amgad a példákon.
mellesleg, valaki megy holnap középiskolás megméretkezni a második menetben? ;) -
belluci88 #1352 segítsen valaki.lécci:( fontos lenne -
belluci88 #1351 1, egy trapéz párhuzamos oldalai 34 és 17. a trapéz átlói merőlegesek egymásra. a trapéz egyik szára 964gyöke. mekkora a másik szár, a terület és a trapéz magassága?
2, bizonyitsuk be, hogy a 37, 537, 5537, 55537, 555537... sorozatban végtelen sok összetett szám van!
3, bizonyitsuk be, hogy ha négy egymást követő természetes szám szorzatához 1-et adunk, egy természetes szám négyzetét kapjuk!
előre is köszi:D -
colos2 #1350 Igazad van! benéztem a példát! 
Én 3 KŐR(!)-re gondoltam, amik közé 1 kis kört kell beilleszteni! Inkább alszom egyet...aztán megnézem úgy...
-
Thibi #1349 izé
R*2/gyök3=R*2*gyök3/3=(2/3)*gyök3*R (ugye gyök3/3=1/gyök3)
és nem R+r egyenlő ezzel a távolsággal ,csak felülről látszódik R*2/gyök3-nak a két gömb távolsága. Rajz nélkül nehézkes magyarázni: van egy derékszögű háromszög: a nagyobbik befogó R*2/gyök3, a kisebbik befogó az oldalról nézve R-r távolság, az átfogó pedig a tényleges R+r távolság. Ezekből pitagorasz tételével jön ki a r=R/3
(próba: van három kb 6 centi átmérőjű teniszlabdám, csináltam egy 2 centi átmérőjű galacsint, nagyjából beillik a teniszlabdák közé) -
colos2 #1348 Ne haragudj thibi, de a megoldásod nem jó. (szerintem) Onnantol van gond, hogy a "R*2/gyök3 távolságra látszódik a nagykör középpontjától", ugyanis az a távolság (2/3)*gyök3*R, így R+r=(2/3)*gyök3*R, átrendezve; r=R*((2/3)*gyök3-1)
Kifejtve: Az oldal 2R. A 3szög egyenlő oldalú, így a szögei kivétel nélkül 60 fokosak. A szögfelező legyen X. Akkor Cos30=X/2R; Cos30=gyök3/2, így X=2R*(gyök3/2). A szögfelezők jelen esetben azonossak a súlyvonalakkal, amiből kifolyólag 3-adolják egymást! Nekünk a hoszabbik oldala kell, így szorozni kell 2/3 -al.
R+r=(2/3)*2R*(gy3/2)=(4/6)*gy3*R=(2/3)*gy3*R. Ezt az egyenletet átrendezve kaphatod az r=(2/3)*gy3*R-R, leegyszerűsítve r=R*((2/3)*gy3-1), pofonegyszerűsítve pedig az r=0,1547*R közelítő eredményt.
-
yanus #1347 hi all, tud vki Eviews5.0-hoz serialt.. pls fontos lenne.. előre is köszi... msn címem: [email protected] -
pista007 #1346 nincs iskola, nem kell matek leckét oldani->pangás a fórumon... -
Thibi #1345 R/3?
A három nagy gömb középpontjai 2R távolságra vannak egymástól,felülről nézve egy 2R oldalú szabályos háromszöget alkotnak,a kiskör középpontja felülről nézve a a szögfelezők metszéspontjában van,vagyis R*2/gyök3 távolságra látszódik a nagykör középpontjától ,a tényleges távolság R+r,oldalról nézve pedig R-r a köztük levő távolság, ezekből pitagorasz tételével azt hiszem az jön ki,hogy r=R/3 -
#1344
Egy asztalon három egyenlő R sugarú gömböt úgy helyeztünk el, hogy azok páronként érintik egymást. Mekkora annak a kis gömbnek a térfogata, melyet a három gömb közé illeszthetünk az asztalra őgy, hogy mindhárom nagy gömbör érintse? -
#1343
Ez is jó sztem. -
#1342
Szerintem is 1/2 az ötödiken a megoldás -
Thibi #1341 befogókról és átfogóról beszél, vagyis derékszögű háromszög (a c szög a derékszög) -
belluci88 #1340 ABC háromszögben a szög=30° az AB átfogó felezömerölegese az AC befogót K-ban metszi. milyen arányban osztja K az AC befogót? ez nem kevés adat? a c szöget nem tudjuk és igy az oldalt sem.és igy nem tudom az arányt. -
#1339
Sziasztok!
Az történt velem a minap hogy matektanárom nem fogadta el a dogám egyik megoldását de csak itthon vettem észre, hogy (szerintem)rosszul javított.
Itt a feladat:
"Egy szabályos dobókockával egymás után 5x dobva mennyi rá az esély hogy a kapott számok mindegyike páros lesz?"
Így oldottam meg: Egyszer dobva ennek esélye 3/6 azaz 50%
5x dobva ennek esélye (3/6)*(3/6)*(3/6)*(3/6)*(3/6), azaz 0,03125 vagyis 3,1%
Így oldottam meg de sztem vmit benézhetett, legalább is remélem. Ha én szúrtam el vmit kérlek részletesen magyarázzátok el. -
#1338
(1/6)^6
mert:
első dobása az fix, hozá képest a második ember első dobása ugye 6 féle képpen következhet be, amiből csak 1kedvező, amit az első dobott. Első ember második dobása is fix, és ahhoz is hasonlóan tud dobni a második ember.
szinte teljesen biztos vagyok ebben, ha valaki esetleg nem giy gondolja, kérem jelezzen!
de! meggyőztem magamat. képzeljüök el az első ember 6-os sorozatát. namost, összes lehetőség amit a második dobhat 6^6, és ebből neki csak 1 a jó, amit az első dobott. -
Nuki #1337 Csak neked, én valami nagyobb hülyeséget írtam 
-
#1336
nekünk az ötletünk (2/36)^6-on volt, de ne kérdezzétek miért...:D -
Nuki #1335 Sziasztok!
Ez nem egy matekpélda, hanem egy megtörtént eseményt dolgoz fel, szöveges példa szerűen.
Két ember dob hatoldalú kockával. HATSZOR egymás után ugyanannyit dobtak (mindaketten például 3-1-2-6-5-2). Erre mekkora volt matematikailag az esély, hogy bekövetkezzen?
-
#1334
szerinted?
[URL=http://www.sg.hu/listazas_msg.php3?id=1067516807&no=1317]#1317[/URL] -
ProXero #1333 Ez könnyebb, mint gondoltam. Egy négyzetszám nem végződhet 7-re, és ha n>4 , akkor n! 0-ra végződik. Meg kell még nézni az összeget n=1,2,3,4-re, és kész.
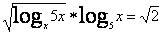[/IMG]