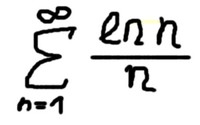4415
Matematika feladatok
-
 #2252
#2252
Hi!
Már lényegtelen, nem lett volna jó a keresett állításom.. -
 #2251
#2251
ne használd az imageshacket, sz@r az. használd a tinypic -t. -
ba32107 #2250 Szúrd be újra a képet máshonnan, nem látszik. -
 #2249
#2249
Hi!
Középiskolában 9.es vagyok, és lenne egy kérdésem( egy feladatmegoldáshoz kellene): Ha ez az állítás igaz, akkor rájöttem a megoldására:
Link
Látszólag egyszerűnek tűnik, de mégsem az..Megpróbáltam elindulni az a·(2k+1)+b·(2k+1) -nek az általánosításából, de nem jött össze, bár én még kitartok amellett hogy az utóbbinak köze lehet az előző példának az általánosításához..Tudnátok nekem ebbe segíteni?
Megjegyzés: a függőleges vonal az oszthatóságot jelöli.
Előre is köszi. -
 #2248
#2248
egy másik lehetőség, hogy írsz egy egszerű programot, amely alapvetően 9 ciklusból és 1 feltételvizshálatból áll és (10^9=) 1 000 000 000 itárációból megmondja az eredményt. az összes lehetségest.
ne aggódj, gyorsan lefut. -
 #2247
#2247
jelöljük a négyzeteket sorra a,b,c,stb-vel balról jobbra, fentről lefelé haladva.
az egyenletek:
(1) a/b+c=8
(2) d+e/f=2 (vajon jó ez az egyenlet?)
(3) g*h-i=1
(4) a*d-g=3
(5) b+e-h=8
(6) c-f+i=9
6 egyenlet, 9 ismeretlen.
de ugye feltételezzük, hogy minden ismeretlen nem negatív, egész és nem nagyobb mint 9.
és amit még tudunk:
a/b=egész, tehát vagy a=0, vagy a=b, vagy b=1, vagy (a=4 és b=2) vagy (a=6 és (b=2 vagy b=3)), vagy (a=8 és (b=2, vagy b=4)), vagy (a=9 és b=3) (1)
e/f=egész, tehát vagy e=0, vagy e=b, vagy f=1, vagy (e=4 és f=2) vagy (e=6 és (f=2 vagy f=3)), vagy (e=8 és (f=2, vagy f=4)), vagy (e=9 és f=3) (2)
g*h=i+1, mivel i<=9, i+1<=10, tehát g*h<=10 (3)
a*d-g=3, mivel g<=9, g+3<=12, tehát a*d<=12 (4)
b+e-h=8, mivel h<=9, h+8<=17, tehát b+e<=17 (5)
c-f+i=9, mivel f<=9, f+9<=18, tehát c+i<=18 (6)
most egyenletrendszerként kellene kezelni az egyenleteket (összeadni kivonni párosával, mindegyiket felhasználva), majd az így kapott egyenleteket újra megvizsgálni.
de ezt már rád bízom, hiszen láthattad a módszert.
ha elég sok feltételt írsz fel, akkor előbb utóbb megkapod a megoldás(oka)t.
-
tivadar89 #2246 Üdv, a következő feladatban kérnék segítséget. A sor konvergenciasugarát és konvergenciaintervallumát kell meghatározni. Az y sor konvergencia tartományát sikerült meghatároznom (remélem jól), de itt elakadtam. Az y=(3x-3)^2-ba kellene behelyettesíteni hogy megkapjam x-re a konv. intervallumot ? Ha igen akkor ezt hogyan lehet megoldani ?
-
 #2245
#2245
szerintem csak számjegy! -
 #2244
#2244
és egy "kocka" az egy számjegy, vagy tetszőleges pozitív szám állhat ott, esetleg egész negatív is lehet, vagy bármilyen valós???? Mert akkor mindjárt más a helyzet... :P -
 #2243
#2243
sajna én nemtudom megcsinálni:D gimiben max. 3 ismeretlenes egyenletrendszereket tanultunk!
szeretném ha valaki megoldaná nekem ezt a feladatot -
 #2242
#2242
elnevezed az ismeretlen számokat betűknek mondjuk a-tól i-ig.
majd felírod a 6 egyenletet 9 ismeretlennel és megoldod. -
 #2241
#2241
valaki segitene ezt megoldani?megköszönném! -
tivadar89 #2240 Köszi, sikerült megoldani integrálkritériummal. Divergens a végtelen sor. -
ba32107 #2239 f(x) = ln(x) / x, x e [1,oo] monoton fogyó, alkalmazható az integrálkritérium, mely szerint:
Integrál 1-től végtelenig f(t) dt ekvikonvergens Szumma n=1 végtelenig f(n). Tehát kiintegrálod az improprius integrált, megvizsgálod a határértéket, és megvan, hogy konvergens-e a végtelen sorod. Ezt most nincs kedvem megcsinálni. -
ba32107 #2238 Szerintem integrálkritériumra van szükséged, de ha lelőnek se jut eszembe, hogy van az a tétel :/ -
tivadar89 #2237 A következő feladatban azt kellene eldönteni, hogy a végtelen sor konvergens-e vagy sem. (indoklással)
Próbálkoztam a gyökkritériummal, de a határérték=1, ezért a módszer nem alkalmazható. A hányadoskritériummal szintén nem sikerült eredményt produkálni. -
adamo07 #2236 :) köszi -
ba32107 #2235 Hát kérdezd meg a matektanárodat -
 #2234
#2234
én ilyen oszthatósági szabályokat mondanék pl. a ha a szám számjegyeinek összege osztható 3-mal akkor a szám is és bebizonyítanám. -
Bor1sz #2233 Nem neked szólt. Komment alatt: Válasz 'sovatalevi' üzenetére (#2229)
Amúgy oszthatóságról most hirtelen a diofantikus egyenletek ugranak be. -
adamo07 #2232 Nem azért kérdeztem mert nincs kedvem dolgozni ezzel, hanem mert nem találtam hozzá olyan anyagot :/ -
ba32107 #2231 Mert nincs kedvünk lusta disznók helyett dolgozni? -
adamo07 #2230 sziasztok! Segítségeteket kérném abban ,h matek emelt szintű érettségin mit említenétek meg az oszthatósággal kapcsolatos problémákhoz ?előre is köszi -
 #2229
#2229
de miertt nem?ha ertitek miert nem?nem buknak mek matekbol. -
ba32107 #2228 Ha nem értesz valamit, és máshol nem találod a megoldást, elmagyarázzuk, de nem napi ötször, és nem oldunk meg teljes feladatokat sem. -
 #2227
#2227
de cssak azt kene amit nem ertek. -
 #2226
#2226
Természetesen nem. A házi feladat azért van, hogy gyakorolj, és ne maradj ostoba. -
 #2225
#2225
8cadikos hazikrol lenne szo -
 #2224
#2224
Hali ha megkezdodik a suli es irok ide matek hazikat akkor aki erti megoldja? -
#2223
meglett az analízis kettes ma 
szóval nem voltak hiábavalók a válaszok, köszi:)) -
 #2222
#2222
Megoldottam, ki is jött, NAGYON KÖSZÖNÖM! 


-
Thibi #2221 aha -
 #2220
#2220
Köszi szépen! 
Akkor ha jól értem a függvény lokális maximumát kell megkeresni,0-100 értelmezési tartományban. Jól értem? Bocs, csak biztosra akarok menni, ezen az egy feladaton két jegy múlik. -
Thibi #2219 profit = árbevétel-költség = 250q-(100q+q*q+100)
ennek kell a maximumát megkeresni 0 és 100 közötti q értéknél
-
 #2218
#2218
q*q az természetesen ,,kúnégyzet", csak nem tudok a felső indexbe írni 
-
 #2217
#2217
Sziasztok!
Pénteken vizsgázom analízisből, és a mintafeladatsoron van egy példa, amit senki nem tud, hogyan kell megoldani (mivel nem vettük órán), és ezért jár a legtöbb pont:
Az alábbiakban adott termelési függvények alapján határozza meg azt a kibocsátási szintet, ahol a profit maximális. Vegye figyelembe azt, hogy a technológia maximum 100 egység kibocsátását teszi lehetővé.
Költség függvény: K(q)=100q+q*q+100
Bevétel függvény: B(q)=250q
Nagyon megköszönném, ha valaki tudna segíteni, hogyan kell megoldani ezt a fajta példát. Egyik csop.társ szerint csak egyenlővé kell őket tenni és kiszámolni a q-t, de mivel több pont jár érte, mint egy teljes függvényelemzésért, vszínű nem ilyen egyszerű a dolog.
-
lally #2216 Bocsi én is , hiszen kétszer vettem a felét! -és még
Qetuol nevének elírásáért is Mea Culpa:
t= 16/3
Köztes területük így kereken = 6,25 - 5,3 = 0,95 területegység. -
#2215
köszi all -
lally #2214 Akkor foglaljuk össze:
{Ba32107; Jól kezdted, csak be kell helyettesítened az x=1 helyen.)
Quteol pedig még fejben is jól számolt.}
y'= - 2x
m = -2*1 = -2 iránytangenssel.
Az egy ponton átmenő egyenes egyenlete így tehát:
y = -2x +5 azaz a tengelymetszete 5 egység,
az x-et pedig: +2,5 döfi.
Az első térnegyedben van tehát egy háromszögünk, mely területe
T = 6,25 területegység.
Ebből kell kivonni a parabola alatti területének FELÉT, hiszen csak az első térnegyedéről lehet most szó!
Integrál 0-tól 2-ig tehát: = 16/3 területegységnek a fele:
t= 8/3 egység.
Köztes területük így kereken = 6,25 - 2,67 = 3,58 területegység.
-
uwu #2213 Egyszerűbb mint integrálgatni.
Lerajzolod, és fejbe kiszámolod.