4415
Matematika feladatok
-
lally #2735 Viccelődtök megint? -ugye!
(-annó, a 60-as években még tán "technikumi_felvételiként" is szerepelt.
Csak azért minősíteném még "gimi-elsősnek" ezt a példát, mert nem ártana a végén majd egy gyöktelenítés is!)
Nem írtam el tegnap a; #2728-at! -'Eli Jah' üzenete volt az még, eredetileg. -
 #2734
#2734
Ja tényleg, n azt hittem, hogy középre van kötve. -
Candi #2733 Ez csak abban az esetben igaz, ha a kecskét nem a kerítéshez akarja kötni, hanem a terület egy olyan pontjára, ahonnan a kecske éppen nem éri el egyik kerítést sem (mondjuk a terület közepére szúrja le a karót, vagy annak a közelébe).
-
 #2732
#2732
megoldás a fizika topigban -
 #2731
#2731
a=r^2*pí
a/2=x^2*pí
x-et keresed, a helyére azt raksz amit akarsz, az r meg ennek függvényében valami. -
 #2730
#2730
a feladat: adott egy kör alakú kert, körbekerítve. a gazda kiköt egy kecskét belülről a kerítéshez. milyen hosszó legyen a kecske kötele, h legfeljebb a kert felét tudja lelegelni. -
lally #2729 -sőőőt:
Tegnap este ezen a régi_2728-as számon még "Miszter Bííín" táncos képe, egy jót vigyorgott is! -
 #2728
#2728
kár, h kimaradtam a #2724-ből 
-
lally #2727 -időnként tényleg nem tudom; Mikor is poénkodtok, mer' ...
Polár-koordinátákból integrállal (is) levezethető a:
KÖR_Területe (-amely, állítólag) = D*D*(Pi)/4 (; hiszen a köröknek, Csak az átmérője mérhető! -> tényleg butaság tehát az R^2* pi lexikális-képletet megjegyezni. -mondá dr.Magyar Bálint bá' ?!)
Köszi a megtisztelő "fejezést", de az én_pici-bucim, tán pöttyet jobban mutat a "privát-nyakamon".
-
polarka #2726 r és α a kecske-, R és β a kert köréhez tartozik. -
polarka #2725 Én eddig jutottam a cos-tételből és a terület képletből:
-
#2723
igen, gyakorlatilag ugyanaz :) -
polarka #2722 Nekem úgy érthetőbb a dolog, h 10 db pont jelöli a söröket és közéjük húzzuk az embereket jelképező strigulákat. Egy vonaltól a tőle balra levő vonalig levő pontok száma az adott embernek jutó sör. A jobb végen mindig lenne egy strigula, tehát azt nem vesszük számításba. így 10pontot és 19vonalat kell sorba rendezni. Ami ismétléses permutáció, vagyis 29!/(10!*19!)= 29alatt a 10(vagy 19). -
chelseadrukker #2721 Á köszönöm:D -
pet0330 #2720 Szia!
Na fogod és összeadod azokat hogy meik nyelvet hányan tudják, ezzel megkapod hogy hány embernek kéne lenni összesen.
Ebből kivonsz 32-t mert 1 nyelvet mindnki tud.
Kivonsz még 8-at mert 8-an +1 nyelvet is tudnak.
És a maradékot elosztod 2-vel mert ők +2 nyelvet tudnak.
Ez 3, tehát 3-an tudnak 3 nyelvet, 8-an 2-t és 21-en 1-et.
Ell.: Ha az embereket adod össze akkor az 32-lesz , ha pedig a nyelvtudást akkor 46 ami a 3 nyelv összege tehát jó. -
chelseadrukker #2719 Sziasztok, nekem is lenne egy kérdésem.
Van 32 fő, mindenki tanul legalább egy nyelvet.
Angol: 17
Német: 14
Francia 15
Pontosan két nyelvet tanulnak 8-an.
És ennyiből kellene megtudni hányan tanulnak 3-om nyelvet?
Ha valaki tud segíteni légyszi írja le aztis hogy erre hogyan lehet rájönni. -
#2718
kicsit késve, szori:
képzeljük el, hogy a 20 ember nevét föl írjuk egy-egy egyforma cetlire (amik közt később nem teszünk különbséget) és kirakjuk egymás mellé az asztalra. most a cetlik után húzogatjuk a strigulákat, hogy ki hány sört kap. behúzzuk mind a tízet. így egy "30 hosszú jelsort" kapunk (cetlik+strigulák), amiből 20 cetli. az első nem lehet strigula, csak cetli, mert utána húzzuk be a strigulákat, tehát azt ne is figyeljük. így csak azt kell megnézni, hogy a 29 maradék "jel"-ből hányféleképpen tudom kiválasztani a cetliket/strigulákat. így lesz 29 alatt a 10 illetve 29 alatt a 19. -
 #2717
#2717
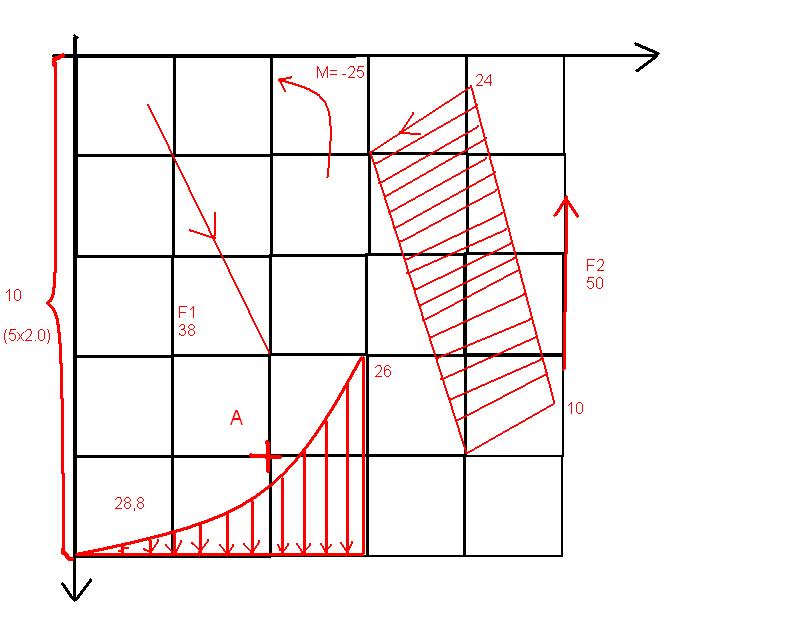
hi!
mechanikai feladatban segítene valaki? kaptam egy ilyen jegyzetet és szeretném hogyha valaki segítene megállapítani az eredőket, és az erőkart!
-
Notram #2716 Igen, erre már rájöttem én is, de Te adtad meg a kezdőlökést…  Akkor valahogy nem ugrott be, hogy az első n tag összegképlete lesz a megoldás.
Akkor valahogy nem ugrott be, hogy az első n tag összegképlete lesz a megoldás.
-
 #2715
#2715
szerintem is 
-
 #2714
#2714
na ja... 
a NUMB3RSben Csárli azt mondta (S2E3), h egy század fokra kiszámolja fénykép alapján. Az kb 1-1.5km pontosság. Szerintem kamuzik a kis fürtös... -
 #2713
#2713
de hát annyira nem rossz, végülis az ország passzol (többé-kevésbé) ^_^ -
 #2712
#2712
Amúgy én nagyon szájbarágtam ezt a megoldást, mert 2009db egymás utáni szám összege(S), ha a legelső a[0]:
S=2009*((a[0]+(a[0]+2008))/2, ami:
S=2009*(a[0]+1004) és innen már látszik is... -
 #2711
#2711
Dunaharaszti - de ha Szigetszentmiklóst megkeresed, akkor az majdnem ugyanaz - egyszóval messze van :(((
Nagyon gyanús nekem, h a számítást barmoltam el, holnap kicsit átbogarászom és jövök, ha lesz valami... Ennyire rossznak azért nem kellene lennie... :( -
Scorpus #2710 Sziasztok!
Kérlek segítsetek az alábbi lineáris algebra feladatok megoldásában! Nagyon fontos lenne!
1. Mutassuk meg, hogy nxn-es valós felső háromszög mátrixok vektorteret alkotnak, adjunk meg bennük bázist, adjuk meg a tér dimenzióját R felett! (R - valós számok halmaza)
2. Bizonyítsuk be, hogy az F = {a+b*gyök2 | a,b ε Q} halmaz test a szokásos műveletekkel!
(Itt azt kell bebizonyítani, hogy ez a halmaz egy test. Ez akkor test ha értelmezve van rá 2db kétváltozós művelet és egy rakás axióma, de az a baj, hogy ezeket nem tudom hogy írjam le matematikailag)
3. Adjuk meg az alábbi lineáris leképezések mátrixát a standard bázisban! Adjuk meg a leképezés sajátértékeit és sajátvektorait, sajátaltereit; magterét és képterét és ezek dimenzióját!
a) R3 pontjainak z tengely körüli elforgatása α szöggel.
b) R3 pontjainak xy síkra való tükrözése.
c) R3 pontjainak xy síkra való vetítése.
d) R3 pontjainak z tengely irányú 3-szoros nyújtása.
e) R3 pontjainak tengelyre való tükrözése.
f) R3 pontjainak tengelyre való vetítése.
4. Az előző feladatot módosítsuk úgy, hogy a forgatás, tükrözés, vetítés tengelye illetve síkja általános helyzetű, de továbbra is 0-n átmenő legyen! (pld. (1,1,1))
Házi feladat része ennek: ilyen irányvektorú egyenesre való tükrözés.
Ha bárki bármelyik kis részében is tud segíteni, annak nagyon megköszönném! :) -
 #2709
#2709
a térképen be van jelölve a valódi helyzeted, hogy össze lehessen vetni? vagy csak én nem látom :/ -
 #2708
#2708
Na, igaz késve, de megcsináltam tisztességesen és jött a kiértékelés és a nagy pofáraesés a végén, de azért jó volt:
0.) Most hétvégén gyönyörű napos idő volt mifelénk, így gondoltam, megcsinálom a mérést. Az is e mellett szólt, h most van az őszi napéjegyenlőség ideje, érdekelt, mennyire sorjáznak az árnyék végpontjai egy egyenesen és mennyire K-Ny irányba. Tehát a mérés helye Dunaharaszti és kihasználva a környékbeli füves területeket, kivonultam egy nyugis helyre most 20-án.
1.) A mérési elrendezés
Lehet látni, hogy kellett a méréshez először is egy GPS, hogy tudjam merre vagyok. :P A lap szélének irányát kimérni egy tájoló, egy buborékos vízszintező, amivel a lapot síkba állítottam, egy árnyékvető, ami egy radírba lehető legpontosabban merőlegesen beleállított sasliknyárs volt és egy vonalzó, amivel lesimítottam az árnyék környékén a lapot, ha feldudorodott volna.
2.) A kapott mérési pontok
Jól látszik, milyen szépen sorjáznak a pontok egy vonalban. Tapasztalat: az árnyék vége NAGYON NEHEZEN jelölhető be, akár +-2mm-t is lehet bizonytalankodni és szinte biztos, hogy rövidebbnek jelölöm, mint hosszabbnak.
Negyed óránként mértem egyet és addig folytattam, míg a környékbeli házak be nem árnyékolták a kis asztalt.
3.) A kiszámolt koordináták a térképen
Ez bizony jól mutatja, hogy a gondos tervezés és alapos kivitelezés ellenére rohadtul nagy szórással tudtam csak meghatározni a helyet. Az összekötése a pontoknak (É-ról D felé) az időrendi sorrendet is jelöli, ahogyan egymást követék a mérési pontok. A számítás nem is volt olyan egyszerű én rábíztam a Maple-ra, de még át kell újra néznem, mert egy közelítő Nap pozíció számító módszert használtam, ráadásul olyat, ami 1978-as irodalomból származik, így a benne szereplő konstansok már mások lehetnek - mindenesetre ez az első eredmény, bízom benne, talán nem a mérés ennyire pontatlan... :(((
A napokban, vagy a köv. hétvégén tervezem, hogy megismétlem, még gondosabban, hátha lehet kicsit csiszolni már az adatgyűjtéssel is... -
 #2707
#2707
:) tudom én, no problem! 
-
 #2706
#2706
csak vicc volt, "amint azt az ábra is mutatja" 
-
 #2705
#2705
ejnye, no... ;) :)
nemúgy dőlt, h xar -
 #2704
#2704
dehát most mondja h dől ^^ -
Notram #2703 Köszönöm a választ! 
-
 #2702
#2702
ejjj, de bebuktam a b.) pontban, ott az általános tag így néz ki:
a[_i_]=a[0]+i
a "szögletes zárójelben az i" miatt lett az egész dőlt onnantól :( -
 #2701
#2701
a.) Legyen az összeadandó 2009 darab szám a[0], a[1], ..., a[2007] és a[2008].
b.) Ekkor a[1]=a[0]+1, a[2]=a[0]+2, ..., a[i]=a[0]+i, ...
c.) Ezeknek az összege: a[0]+a[1]+...+a[2007]+a[2008], ami a b.)-t felhasználva írható:
d.) a[0]+(a[0]+1)+(a[0]+2)+...+(a[0]+2007)+(a[0]+2008), amiből a[0] kiemelhető:
e.) 2009*a[0]+(1+2+...+2007+2008). Ez utóbbi pedig felhasználva a számtani sor összegképletét:
f.) 2009*a[0]+2009*(2008/2), amiből 2009-et lehet kiemelni:
g.) 2009*(a[0]+1004). Amiből már látszik, hogy ez a szám nem lehet prím, mivel a 2009 már biztosan osztója, tehát nem lehet 2009 egymás utáni egész szám összege prím. -
Notram #2700 Lenne egy "gyors" kérdésem:
Lehet-e 2009 egymást követő egész szám összege prímszám?
Biztos van a megoldására valami egyszerű módszer, de most nem pörög eléggé az agyam… :S -
polarka #2699 A 2100 nem megfelelő, ez könnyen belátható abból, h a számjegyek összege 4 kell legyen. Benéztem. -
 #2698
#2698
:P kééééreeeem, lécci, lécci, lécci!!!!! ;) -
#2697
ennek van egy ragyogó "cédulásos" magyarázata, amiről nagyon jól meg lehet jegyezni és mindig eszetekbe fog jutni :C
ha valaki nem ismerné és érdekli akkor előkaparom -
polarka #2696 Köszi, a név alapján utánanéztem.
És látom, h ismétléses permutációra vezethető vissza az egész. így már tiszta. -
 #2695
#2695
ismétléses kombináció:
itt n = 20, k = 10 , tehát 29 alatt a 10, ami ugyanaz mint 29 alatt a 19