4415
Matematika feladatok
-
 #452
#452
HELP! Egy béka 5mp alatt 2m úszik, liba 2mp alatt 5m-t úszik. De a liba csak 42mp után indul el.
Kérdés: mikor éri utol a liba a békát?
Grafikonom szerint 50.mp-nél éri utol, de az egyenletet nemtom felírni.
THX!
-
 #451
#451
Gyökvonás előtt el kell gondolkozni:
a^2 = b^2-ből nem következik, hogy a = b, hanem csak az, hogy
a = b vagy a = -b!
Hát itt pont ez utóbbi igaz, hiszen 4 - 4,5 = -(5 - 4,5).
-
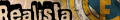 #450
#450
16 - 36 = 25 - 45
Most adjunk mindkét oldalhoz (9/2)2 -t !
16 - 36 + (9/2)2 = 25 - 45 + (9/2)2
Vegyük észre, hogy mind két oldalon teljes négyzetet látunk !
[4 - (9/2)]2 = [5 - (9/2)]2
Vonjunk, mindkét oldalból gyököt !
4 - (9/2) = 5 - (9/2)
A baloldalon szerepel 4, amiről tudjuk, hogy 2x2
2x2 - (9/2) = 5 - (9/2)
Adjunk mindkét oldalhoz (9/2)-t !
2x2 = 5 ??!! J
-
 #449
#449
Igazából nem tudom! Ezt a kérdést én is csak láttam és megtetszett, ezért gondoltam hogy felteszem itt! -
 #448
#448
bizonyítható, hogy nincs? -
 #447
#447
Lássuk a bizonyítást! Tehát a bizonyítandó
Áll.: nem létezik olyan a és b egész számok, hogy:
1. abs(a^2-b^3) = 2
2. a <> 5, a <> -5
3. b <> 3
Az, hogy "nem találtunk más megoldást, ezért nincs is", még nem bizonyítás. -
 #446
#446
Nincs :)
Ügyes!!! Hogy jöttél rá? Számolgattál egész nap? -
 #445
#445
26 on kívül még van más? -
 #444
#444
Szerintetek hány olyan szám létezik, aminek a szomszédai egy négyzetszám és egy köbszám? (honfoglalóban volt kérdés) -
 #443
#443
az ötösnél valszeg nem látod át mi is a feladat...
az a.) kérdésnél aszogya a=2
így a feladat:
1: kösd össze az origót a (2;4) ponttal
2: keresd meg azt a f(x)=x2 függvényt, ami átmegy az origón és a (2;4) ponton.
így má megy?
nem látod a függvényt? használd a GCalc progit! -
 #442
#442
na jó... legyen a négyes.
vezessük be az a=köbgyök3+1 jelölést
így az egyenlet (gyök(a))6-3*(gyök(a))4+3*(gyök(a))2
ami ha a gyökök kioltják a hatványok egy részét, akkor az a4-3a2-3a marad.
ez már elég egyzserű, ugye?
további segítséget itt találsz.
-
 #441
#441
akkor má megvan az elégséges, nem? ;-)
-
misi007 #440 1es, 2es, 3as, 7est meg tudtam csinálni.
A többihez kellene segítség. -
 #439
#439
nekem úgy tünik, hogy meg se próbálod. ha pedig neked ilyen a hozzáállásod, akkor másoktól miért várod, hogy lelkesedjenek?
ráadásul ha télleg ennyire sík vagy az egészhez, akkor jogos az érdemjegy, nem? -
misi007 #438 csak 1-2 feladatot lécci -
misi007 #437 szinte egyiket sem tudom megcsinálni
Lécci egy-két feladatot megcsinálnál nekem!!
Jegyet kapunk rá, de nemtok semmit. Holnapra kellene
Csak hogy 2es vagy 3as legyen -
 #436
#436
konkrétan melyik feladattal, konkrétan hol akadtál el? -
misi007 #435 az is elég ha 3ast kapok, csak lécci segítsetek -
misi007 #434 Bocsi, elírtam.
Nem vágom az egészet!!!!! -
misi007 #433 Helló!
Segítségre lenne szükségem a következö feladatsor megoldásaival kepcsolatban. Meg kell csinálnom, de vágom.
Köszi a segítséget.
feladatsor -
 #432
#432
help me.
pitagorasz tétele:
ezt hogy oldom meg?:SSS -
Liliomfa #431 gézu de kis gonci vagy :)))) -
Gézu88 #430 A 0 pont a legjobb azzal egyből híres leszel a sulidban 









-
 #429
#429
Így is úgy is 1-es lesz, csak nem mind1 hány ponttal:(
-
Zsoldos #428 Nyisd ki a konyvet es nezd meg. Nem bunkosagbol vagy lustasagbol mondom, max ugyanazt fogja leirni barki, mint ami abban van es te sem leszel okosabb.
Ha megtetted es nem ertheto akkor kerdezz arra a reszre amit nem ertettel, es akkor van ertelme a dolognak. -
 #427
#427
Vki elmagyarázna a vektoriális-szorzatot?
-
 #426
#426
THX!!
-
 #425
#425
Köszi a válaszokat!
Az igazsághoz az is hozzátartozik, hogy két kérdésnél nem teljesen vaktában tippeltem, de azért így is nagy szerencse. :) -
 #424
#424
7 kérdés, kérdésenként 4 választási lehetőség, és csak 1 jó közülük.
Legalább 5 jó válaszhoz: (1/4)^5 = 0,00098
Ebben benne van az a lehetőség is, hogy akár 6 vagy 7 jó válasz is lehet.
Ha az a kérdés, hogy pontosan 5 jó válasz legyen jó, tehát 2 válasz biztosan rossz legyen, akkor: (1/4)^5 * (3/4)^2 = 0,00055 -
 #423
#423
sqrt((8-2)^2 + (3-6)^2) =
sqrt(36 + 9) =
6,71
(Pitagorász tétel) -
 #422
#422
Meg van adva A(2;6) és B(8;3) és elfelejtettem hogyan kell kiszámolni ennek a hosszát :) THX!!
-
Zsoldos #421 "persze tippelhetsz is, annak, hogy két tizedesjegy pontossággal eltaláld az előző feladványod megoldását kb 1/100, vagyis 1% az esélye."
:DD ez nagy igazsag
-
 #420
#420
hogy egyszer helyesen tippelsz a 4-ből, annal 1/4=0.25 esélye van. hogy mégegyszer is, akkor ugye nyolcból kell a megfelelő kettőt.
hét feladatnál ha mind a hét helyes, akkor 7-et kell a 16384-ból kiválasztanod.
5 jó válasz esetén ez az esély annyival változik, hogy a 7-ből hányféleképpen tudsz 5-öt (vagy egyszerűbb, ha kettőt) kiválasztani.
persze tippelhetsz is, annak, hogy két tizedesjegy pontossággal eltaláld az előző feladványod megoldását kb 1/100, vagyis 1% az esélye. -
 #419
#419
most ennek is nagyon örülök :) -
Zsoldos #418 5 tizezred korul, de a lottohoz meg gyurnod kell :) -
 #417
#417
Aki tanult már valószínűségszámítást:
Van 7 feladat. Mind a 7-nél a,b,c,d válaszadási lehetőség van és mindegyikre csak egy jó válasz van. Mennyi az esélye, hogy tippeléssel 5 jó választ sikerül összehozni?
Mert hogy nekem sikerült. :D -
 #416
#416
Ránézésre: x=0 egy megoldás, de vajon van-e több is?
Nyilván x csak -16 és +16 közötti lehet. Ebben a tartományban csak egy maximuma van, ezt könnyű belátni (deriválás), és az pont x=0-ban van, a maximium értéke pedig pont 4. -
Merridious #415 Sziasztok kellene egy kis segítség egy feladathoz Kicsit sürgős.
a feladat = (4. gyök alatt 16+x) + ( 4. gyök allatt 16-x)=4
-
Merridious #414 Sziasztok kellene egy kis segítség egy feladathoz Kicsit sürgős.
a feladat = (4. gyök alatt 16+x) + ( 4. gyök allatt 16-x) -
 #413
#413
nem ellenőriztem a képleteket, de tudunk még valamit.
konkrétan r=1, mivel a feladatban egység sugarú kör van. ha jól emlékszem.