4415
Matematika feladatok
-
Dévidke #532 (3x-4)(x+5)+(2x+10)(x-2)-(3x+15)(x-2)=0
(3x-4)(x+5)+2(x+5)(x-2)-3(x+5)(x-2)=0
(3x-4)(x+5)+(x+5)(x-2)(2-3)=0
(3x-4)(x+5)-(x+5)(x-2)=0
(x+5){(3x-4)-(x-2)}=0
(x+5)(2x-2)=0
ebből következik, hogy
vagy x+5=0 és akkor x=-5
vagy 2x-2=0 és akkor x=1
remélem megfelel
(és, hogy nem szémoltam el ---- este már lassu egy kicsit az agyam) bye -
 #531
#531
(3x-4)(x+5)+(2x+10)(x-2)-(3x+15)(x-2)=0
aki tud segíteni lécci küldjön privit.... -
 #530
#530
Két péklda fut egymással párhuzamosan! -
 #529
#529
Ehh... ez két különböző dolog. Az, amit én itt magamnak fejtegetek egy klasszikus játékelméleti feladat, úgy szerepel a szakirodalomban, hogy "Lady in the Lake". Egy zsenge cicababáról szól, aki egy kör alakú tóban fürdeti hófehér habtestét, miközben orcájára hullnak a szemérem rózsái, mikor a partra pillantva meglátja az ösztönei által hajtott vad szatírt... 
 és szeretné megúszni a kalandot holmi családalapítás nélkül - ki akar jutni a partra és usgyi, pucér seggel rohanás...
és szeretné megúszni a kalandot holmi családalapítás nélkül - ki akar jutni a partra és usgyi, pucér seggel rohanás...
-=ZR=- -
 #528
#528
De jó hogy elovastam megint.........
Megnéztem pontosan mi a feladat.....ÉS:
A hittéritő kannibál rejtély megoldása(nem megoldahatósága)szomszédossági mátrixal. azt meg megoldható......:P -
 #527
#527
A lényeg az lenne h a megoldhatósák szempontjából kéne ebben a mátrixban vmi szabályszerüséget találni. a gráf pedig szerintem az -amiből kreáljuk a gráfot- a két part meg a csónak közötti élek meg a pontok a emberek meg a csónak két helye....Csak az a baj h én irtam má mindenhogy meg prbálgattam....és semmi. Találtam egy mesterséges inteligencíával foglalkozó lapot ahol pont erről volt szó
csak az nagyon kínai.
-
 #526
#526
Lehetne úgy is megfogni a dolgot, hogy beleveszünk vmilyen stratégiát K-nak is, elvégre ő is részt vesz a játékban... Jó-e az mindkettőjüknek, hogy egy időlépés alatt a távolságukat E maximálni, K minimalizálni akarja? Szerintem nem, ugyanis E bármilyen közel lehet K-hoz, addig, amíg a tóban van...
-=ZR=- -
 #525
#525
Amúgy biztos észrevette aki a problémát hétköznapi szemmel nézi, hogy az 1.) stratégia határhelyzete azt jelenti, hogy amennyit K balra mozdul, ugyanannyit mozdul E jobbra (szöget) - és ha nem azonos a középponttól vett távolságuk, akkor aki kisebb sugáron van, az kisebb ívet kell hogy mozduljon. A sebességarány megszabja a sugarak arányát ekkor.
Olyan ez, mint elkapni valakit úgy, hogy szemben állsz vele egy asztal két oldalán és amikor te mozdulsz, akkor ő is, csak ellentétes irányba... Mindenki akarta így elkapni a legjobb csajt az osztályban, nemde...?! ;)
-=ZR=- -
 #524
#524
Én mérnöki szemmel rögvest valami ilyesmit csinálnék: Van két stratégiám:
1.) Maradjunk minél messzebb a kannibál bácsitól és úgy ússzunk
2.) Igyekezzünk úgy kiúszni, hogy úgy érjek partot, hogy a kannibál és én végtelenül kis távolságra legyünk egymástól legalább, hogy a parton már elspurizhassak előle
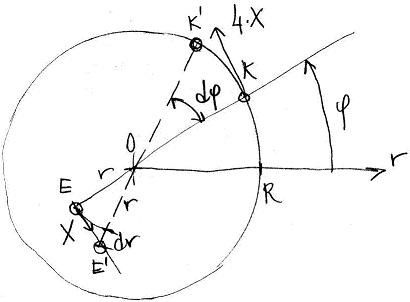
Az első esetet ezen az ábrán lehet látni:
Úgy indul a dolog, hogy a kannibállal (K) ellentétes irányba indul el az emberünk (E). Elemi kis idő alatt K d_fi szöget mozdul el a parton, tehát megtesz R*d_fi utat úgy, hogy igaz R*d_fi/d_t=4*X, merthogy ekkora a sebessége.
Az úszós fickó ezalatt szintén d_fi -t úszik érintőirányba (mert szeretne minél messzebb maradni) és ha még belefér az X sebességbe, akkor a part felé is szeretne d_r -t. Azaz az ő esetében a sebesség úgy néz ki, hogy NÉGYZETGYÖK((r*d_fi)^2+d_r^2)/d_t=X
Namost némi átrendezgetés árárn azt kapjuk ebből a két egyenletből, hogy d_r=NÉGYZETGYÖK((R*d_fi)^2/16-(r*d_fi)^2).
És ez a gyökvonás akkor lehetséges, ha r<=R/4, azaz az 1.) stratégiával a fenti sebességviszonyok esetén csak a tó sugarának negyedéig tud kiúszni, ezután a kannibál mindíg tud úgy helyezkedni, hogy amíg az úszó a legmesszebb igyekszik tőle úszni, addig ő már megint a rámozdulás előtti helyzetbe ér.
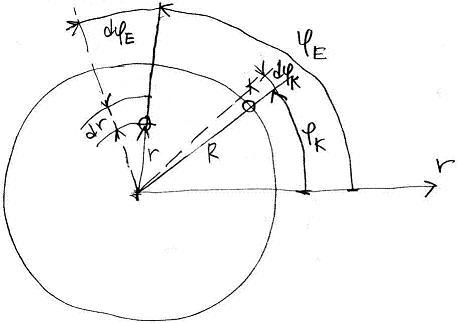
A 2.) stratégiának az a lényege, hogy K-nak és E-nek szabadon változhat d_t idő alatt a szögelfordulása, emiatt megvalósítható(??? ezt még nem írogattam le ???) az az eset, hogy amikor az úszó ember r-je egyenlő R-rel (azaz kiért a partra), akkor a fi_K = fi_E, azaz ugyanott vannak. És akkor illa berek náda kerek 4X+1 -el futás (persze ez a határhelyzet, de ezt kell vizslatni).
Itt van hozzá a hasonló ábra:
Ezt még lehet bogarászni kicsit, az viszont már most nyilvánvaló, hogy kell egy célfüggvény, amit az úszó meg akar valósítani azon kívül, hogy r:=R és hogy fi_E>=fi_K. Mert így nagyon sok megoldás szóba jöhet. Az is jó módszer, hogy a pálya érintőjét állítjuk elő időlépésenként!!! A kezdeti derivált eléggé nyilvánvaló: minél messzebb a gaz K-tól, azaz legyen +végtelen (90fok).
Ennyi egyelőre - remélem a numerikus matekosok ettől beindulnak!
-=ZR=- -
 #523
#523
és mi is a pontos kérdés?
hogy hogyan jutnak át? vagy hogy hánadszorra jutnak át? vagy... ??? -
 #522
#522
-
 #521
#521
-
 #520
#520
Ne lőjétek le a körös megoldását, pls, mert van 2 féle megoldáshoz vezető gondolatfoszlányom - de most meló vala, majd du 5 tájban... Képet lehet asztali gépről beszúrni, vagy csak webről?
-=ZR=- -
 #519
#519
mi a szomszédossági definíciója? -
 #518
#518
először a körös megoldását! :-) -
 #517
#517
Valaki aztat mandja meg nekem h a kannibál misszionárius sztorin - Nem ez hanem a 3 kanniból 3 misszinoárius meg 2 személyes csónak sztorin - Mit ábrázolna szomszédossági mátrixban a megoldhatóság szempontjából?
Mert nekem még elképzelélsem sincs
-
 #516
#516
úgy is megmenekül, ha mindig háttal úszik a kannibálnak. így egyetlen körívet ír le a part felé. -
 #515
#515
sőt, a kis körvonal miatt még kevesebb. -
 #514
#514
ez még csak 3.925X, és a kannibál 4X-el tud menni, szal így még elkapja. -
 #513
#513
na. kb erről beszéltem. -
 #512
#512
mi a megoldás? :-) -
 #511
#511
nem hinném. 4szeres sebességnél a kis kör túl kicsi, nem ér ki időben a partra. persze nagy előnyre tehet szert, és majdnem megvan, de ha 3.14-el számolsz, a külömbség így 0.075 a kannibál javára :-)
persze igazad van, nem tudhatom előre, h a kannibál hogy mozog a parton, a megoldásom csak akkor működik, ha a kannibál mindig a pappal szemben helyezkedik el. vagyis arra a pontra, amerre úszik a pap. de nem látok más megoldást. -
 #510
#510
A dolgot nagyon jól látod.
CSAK:
A lényege végülis az lenne h a tóban van egy a tóval koncentrikus kör melyen belül tudja szabályozni a kanniból hollétét a parton, de azon kivül már csak az érintőre merőleges úszik mivel a legapróbb kanyarodással is csak veszitene előnyéből. -
7evenb #509 ha jól számoltam így ki tud jutni:
-
 #508
#508
szerinrntem:
-ha én lennék a kannibál, akkor általában nem foglalkoznék a hittérítő úúszásának irányával, hanem csak a pillanatnyi helyzetével. megkeresném az úszóhoz legközelebbi szárazföldet és ezt a pontot céloznám be a legrövidebb úton.
-ha én lennék a hittérítő, akkor megpróbálnék olyan útvonalon úszni, hogy a kannibál mindig a legtávolabb legyen tőlem. ez egyébként akkor van, amikor a kannibál a két irány közül nem tud (csak találomra) választani.
mivel a kannibál irányváltása (fordulása) nem kerül időbe, így fölösleges forgatni.
ha létezik megoldás akkor végtelen sok létezik, de a legkézenfekvőbb egy csigavonalú úszás, melynek során a kannibál mindig pont szemben van a hittérítővel (a hittérítő és a köt középpontján átmenő egyenesnek a hittérítőtől távolabb lévő metszéspontján) egészen addig, amíg olyan közel került a parthoz, hogy ha egyenesen kiúszik, a kannibál akkor sem kapja el.
tehát én a feladatot úgy oldanám meg, hogy eleve csökkenteném a kör sugarát annyival, ahonnan a távol álló kannibál még nem kapja (illetve éppen elkapja) az egyenes vonalban úszó hittérítőt.
A kérdés az, hogy az eredeti sugarú körön végzett négyszeres debességű mozgáshoz tartozó szögsebesség meddig nagyobb mint az úszó szögsebessége.
Vagyis:
Ha a kis kör esetén az egyszeres sebességgel leírt mozgás szögsebessége nagyobb mint a nagy körön a négyszeres sebességhez tartozó szögsebesség, akkor a hittérítő megmenekülhet. -
 #507
#507
háát...ha azt nézzük, h a kannibál 4szer olyan gyorsan halad, mint a pap, akkor ez így nem lehetséges. -
 #506
#506
Szerintem kiér mielőtt odaér a kannibál!
Szerintem képletekkel, rajzokkal könnyebben elhinném neked a fenti mondatod! -
 #505
#505
hát ugyebár a körívre a sugár 6.28szor fér rá. ha a koma pont ellentétesen úszik a kannibál elöl, a kannibál ekezd futni az egyik irányba. ha a csávó nem változtat irányt, a kannibál elkapja ez biztos, mert 3.14el kéne minimum gyorsabban haladnia, de ő 4szer gyorsabban is tud. de ha a part előtt közvetlenül megfordul, és az ellenkező irányba úszik, a kannibál nyiván szintén megfordul, és elkezd futni 4X-el vissza, a másik oldalra. közvetlenül miután a kannibál visszaért és megállt, ismét megfordul, és a kannibál is visszafut, de így már lesz annyi előnye az úszó csávónak, h kiérjen a partra a kannibál előtt. így az emberünk, hacsak nem tököl sokat az öltözködéssel, megmenekül :-) -
 #504
#504
Alaphelyzetben van az ember ugye a kör középpontján, a kannibál pedig a kör egy pontján. Az embernek akkor van a legnagyobb esélye kijutni, ha pont hátat fordít a kannibálnak és elkezd úszni, így a kannibálnak meg kell kerülni a fél tavat.
Az ember útja ugye a kör sugara, a kannibál útja pedig a kör kerületének fele.
Ha az ember útja R, akkor a kannibál útja 3,14×R, de 4-szer fut gyorsabban mint amilyen gyorsan az ember úszik, szóval sztem mindenképp elkapja :) -
Dévidke #503 ja azt lehagytam hogy az ellenkező irányba mint a kannibál van kezd el úszni, miután lehagyta! -
Dévidke #502 Boci! Szerintem meg!
Mivel ha a hittárítő el kezd úszni a part felé, de nem úszik ki hanem megáll a tó középpontjétol egy bizonyos távolságre! Ez a távilság éppen akkora, hogy ha ezen a távolságon kezd el körbe úszni, akkor egy picivel gyorsabban teszi meg a köröket mint a kannibál! Namost a kannibáltól így kezd eltávolodi, és mikor már akkorára nöl közöttük a távolság, hogy a kannibál egy negyed... vagy egy teljes fél körrel le van maradva, akkor neki áll úszni a part felé! Szerintem kiér mielőtt odaér a kannibál! Remélem érthető voltam, és nem képletekkel való megoldásra gondoltál! -
 #501
#501
A kedvenc matekpéldám:
Adott egy kör alaku tó melynek közepén van egy ember aki X sebeségel úszik és a parton 4X+1 sebességel tud futni. És Adott a tó partján hirtelen megjelenő kannibál aki nem tud úszni és a parton 4X sebbeségel tud futni.[A kannibál értelmes vagyis: Irányt vált ha kell.]
Megtud E menekülni a hittéritő a kannibál elől?[Az ember nyilván valóan nem egyenesen úszik majd.]
NA? -
Dévidke #500 No problem! You're welcome! :D
-
TomBond #499 Bocsi tényleg elírtam! Nem volt szándékos! A füzetben nekem is (-1;-1) van és még ezek szerint én is ott számoltam el hogy hibásan írtam ki az adatokat.
Még egyszer bocsánat!!
És köszönöm a segítséget. -
Dévidke #498 Így mindjárt más a szitu! :)7evenb-nek igaza van így nem lesz gond az eredményekkel! (Nekem kijött)Kicsit elírtad nekünk a köregyenletet! Számold ét újra az "O" pont koordinátáit! O(-1;-1)Egyébként meg ez egy gáz feladat! Minek kérdez vissza a metszéspontokra! Ki sem kell számolni máskor, csak írd oda, hogy mivel a AB az átmérő, ezért A és B pontok lesznek a metszéspontok! :) -
7evenb #497 szerintem a köregyenlet helyesen:
(x+1)^2+(y+1)^2=40 -
TomBond #496 Nem könyvből van a feladat hanem a matektanár adta fejből: Adott egy háromszög aminek csúcsai A(1;5) B(-3;-7) és C(2;4) Ezekkel kell különböző feladatokat elvégezni.
05. feladat: az AB pontokon átmenő egyenesek egyenlete
09. feladat: az AB szakasz fölé mint átmérő fölé írható kör egyenlete
10. feladat: a 09. feladatban írt kör és az 5. feladatban kapott egyenes metszéspontja
Hát ebből gondolom én hogy ezeknek a megoldásoknak kell kijönni. -
Dévidke #495 semmiféle képp nem jöhet ki az a két metszés pont 40-es sugárral -
Dévidke #494 Rossz a könyved! Ez a megoldás nem nagyon lesz kerek!
-
 #493
#493
meg lehet még oldani grafikusan is, ha egész számok jönnek ki.
alapvetően ez a két megoldás van.