926
Szabad energia, olyan gépek, amelyek sértik az energiamegmaradás törvényét.
-
 #566
#566
Testing a SMOT (egy SMOT vizsgálata) - avagy miért nem örökmozgó a SMOT? -
 #565
#565
Gonoszkodjunk.
Számold bele azt az elhanyagolható csöppnyi dolgot, hogy az egész berendezést fel kell melegítened 381,85-0,000 0001 °C-ra, és azon kell tartanod.
És itt érkeztünk el egy problémához: mint Átlagember is mondta: a kontrolállhatóság kérdéséhez.
Ugyanis egyrészt a 0,000 0001 °C-nyi hőmérsékletkülönbség olyan csekély, hogy bármi kis jelentéktelennek tűnő súrlódás, ütődés, légáramlat befolyásolhatja az egész rendszert - borotvaélen táncoltatva.
A másik probléma a 381,85 °C-ot előállító berendezést a 381,85-0,000 0001 °C-os légtérben kell elhelyezned, illetve a 381,85 °C-ot előállító berendezés működtetése befolyásolja a rendszer (és a rendszer egyes tagjainak) hőmérsékletét, ezért a rendszert külön hűteni kell. A hűtés energiaszükségletet von maga után... -
Albertus #564 Még valami..
Sajnos jelenleg nem ismert olyan szigetelési, erővonal elvezetési eljárás amivel a gravitációs erővonalakat úgy elvezethetnénk, mint ahogy a mágneses erővonalakat..
De sebaj. Mint az smot példája is mutatja, energia termeléshez
elegendő a mágneses erővonalak manipulálása is.. -
Albertus #563 Na ha már itt tartunk... gonoszkodjunk tovább..
Az smot elrendezésnél azt lehet elérni, hogy a gravitációval szemben felgyorsítsuk a golyót, ami lendületbe jön és felfelé gurul a lejtőn..
A térerősség beállításával, statikus mágnesekkel, energia felhasználása nélkül felemeljük és közben még lendületbe is hozzuk szegény golyót..
Igen ám, mondhatnátok, de a golyó eléri elöbb vagy utóbb a felső holtpontot és visszagurul..
No igen.. Ha hagyjuk, hogy a felső holtpont elérése után a másnesek közé érkezzen, mert ha a holtpont elött beleesik egy lyukba ami egy
lejtőpálya felett van, akkor az m tömege és a h magassága, ami a lejtő aljához képest van neki, E=m*g*h energiát is jelent..
Ami a lyuk alatti lejtőbe épített tubinával kinyerhető.. de csak
annyira, hogy a gyorsító vályúhoz azért még oda tudjon gurulni..
Így semmilyen külső energia sem kell.. és mégis működik.. Csupán a mágneses erővonalakat kell úgy vezetni, hogy a felső holtpont közelében már "mágnesesen szigetelt térben" gurulhasson.. -
Albertus #562 Szia!
nem kell szabadkoznod! Nagyon jó az ötleted! -
Albertus #561 Szia!
Jó helyen kapizsgálsz.. Igen, az elrendezés a mágnesgolyóval a rúd tetején, nem a legjobb. Valóban úgy érdemes elrendezni, hogy kétoldalról "mágneses vezeték" mm-ről mm-re csak annyival növelje a térerősséget, amennyi a gördítéshez szükséges.
Így megkapjuk az s-mot elrendezését, amikor az induló térerősség sokkal nagyobb mint az eredeti ábra F pontjánál.. ezért lényegesen magasabbra emeltethető fel a golyó..
A "teljes keresztmetszet" kérdését is jól látod, és majdnem
tovább is gondoltad.. Igen, az egyensúlyi hely ki fog alakulni valahol.. oda kell a lyuk ami kibillenti az egyensúlyból..
Különben ha már ezzel a modellel foglalkozunk, van más megoldása is a működőképessé tételnek, nem csak a Curie ötvözetes megoldás..
Szintén smot-os elrendezéssel, de a lyuknál elhelyezünk egy tekercset
aminek pillanatszerű mágneses tere a golyón kioltja a vontatómágnes térerejét.. és ettől átesik a golyó a lyukon..
Ennek a kioltó mágneses térnek is van energia igénye, de talán meglepő módon, a Curie effektus hőenergia igényének csak a tizede..
-
Locutos #560 Megvallom én is tudom ez egy nagyon leegyszerûsített ábrázolás, ha jól meggondoljuk(meg gyakorlati tapasztalat szerint) nem pont ilyen a mágnesek hatása, megeshet hogy a dolog visszafele menne inkább B-bõl A-ba, attól függõen hogy állítgatunk. Ja es persze több karja is lehet a dolognak... -
Locutos #559 -
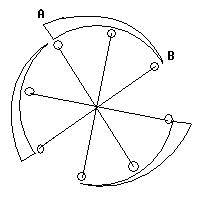
Locutos #558 Igy is lehetne próbálkozni a smot-tal:
remélem megjelenik
Szóval az A ponttól a B pontig fokozatosan csökken a mágneses térerõ.
Ezt ábrázoltam a vékonyodó sávval.
Az asszimetrikusságot úgy is meg lehetne valósítani hogy egyre távolodnának a mágnesek, csökkenve a térerõ. Az A pontban a vonzáskor akkora löketre kell szert tegyen a golyó, hogy mindenképp elégséges legyen a következõ golyó odamozdulásáig(ami ujra erõs vonzásba kerül)
Mi a véleményetek? -
 #557
#557
Egyébként én is ezen a smot-os asszimmetrikus mágneses mezős perpétum mobilén gondolkodtam. Az én elképzelésem szerint a golyót nem kézzel tennénk vissza. Az esés egy pár miliméterrel kisebb lenne az emelkedőnél és egy nagyon alacsony lejtésű, de a mágnesektől messzebb húzódó külső pályán gurulna vissza a golyó a mágneses emelkedő elejére.
Ennek elvileg működni kellene. Ha lesz időm, meg is csinálom. -
 #556
#556
Ja és a felmelegítést nem lehet a teljes térfogaton egyszerre elvégezni, így lesz egy átmineti állapot, amikor az erők kiegyenlíthetik egymást. -
 #555
#555
Ezzel szerintem csak az a gond, hogy ilyen pontos hőmérsékleteket nehéz tartani. Már a surlódástól is több hő keletkezik, és így a golyó a kelleténél hamarabb elveszítheti a mágnesességét. -
 #554
#554
Csináltam egy animált gif örökmozgó animációt. Folyamatosan képes működni és még energiát sem igényel, mert a számítógépem semmivel sem vesz fel több energiát. Élljen a perpétum mobile!

-
Albertus #553 Nos, a számolásod hibájának a számszaki részét nem is néztem..
így még több tiszta energianyereség van..
De nem ez a lényeges, hanem az, hogy egymástól független energetikájú, de egymásra ható folyamatokból lehet sok energiát kinyerni..
Érzékelhető példa: mint a villanykapcsoló.. a kapcsolás energia igénye összemérhetetlenül kisebb a kapcsolt energia nagyságrendjénél..
-
Albertus #552 Szia Te kis hamis!
Ki mondta, hogy szobahőmérsékletről??
Legyen a kiindulási hőmérséklete 381,85-0,000 0001 C fok
ekkor az emeléshez 1298 J/ 1 000 000 = 0,001 298 J kell
Amit a példádban megtermeltettünk: 0,004 664 J
minusz ami a melegítéshez kell = 0,001 298 J
---------------------------------------------------
Tiszta nyereség: 0,003 366 J
Szóval, ha már számolsz... akkor pontosan.
-
 #551
#551
Olyasmiből van sok:
http://www.boatdesign.net/forums/showthread.php?t=14182
http://www.eng.rpi.edu:8080/mdl/update.do?artcenterkey=9
http://foxxaero.homestead.com/indrad_007.html
http://www.memagazine.org/supparch/pejun04/ebursts/ebursts.html
http://www.halfbakery.com/idea/Wind-turbine_20boat
Van napelemes is:
http://www.yachtsales.com/newelect.html
http://www.solarnavigator.net/solar_boats.htm -
HUmanEmber41st #550 Mutattak már régen a TVben egy spanyol fejlesztésű hajót, amit gyak. egy nagy szélkerék=> generátor=> akkutöltő=> akkutelep=> villanymotor hajtott -
 #549
#549
The Museum of Unworkable Devices (a kivitelezhetetlen gépek múzeuma) - további klasszikusok. -
 #548
#548
"A példában emlegetett kerék miért nem működhetne??"
Ezért
Forrás: Lukács Ernőné, Péter Ágnes, Tarján Rezsőné - Tarkabarka fizika, Móra Ferenc könyvkiadó 1972 -
 #547
#547
[url=http://www.lhup.edu/~dsimanek/museum/people/people.htm]Pár "klasszikus"[/url] -
 #546
#546
Hopp, elírtam valamit (nem deltaT-vel számoltam, hanem a végső hőmérséklettel), de ez nem befolyásolja nagyban a dolgot.
Q = c * m * deltaT = 0,444 J/g*K * 4,664 g * 328,85 K = 680,9878 J
Azaz 0,1 s-os felmelegítési idővel számolva a teljesítmény 6809 Watt.
Ez még továbbra is nagyságrendekkel nagyobb. -
 #545
#545
"A mágneses-Curie fémes megoldás szerinted sokkal több külső energiát igényel mint amennyit termelhetne.."
Akkor számoljunk:
Vegyünk egy 1 cm (0,01 m) átmérőjű nikkelgolyót.
Azért nikkelgolyót, mert:
* Ferromágneses tulajdonságokkal rendelkezik.
* Viszonylag könnyű beszerezni, korrózióálló.
* Könnyen elérhetőek róla adatok.
Mennyi munka kell ezen kicsiny golyónak 10 cm (0,1 m) magasra cipeléséhez (ne számoljunk most súrlódást, és egyéb világi hívságokat, az egyszerűség kedvéért)?
A 1 cm átmérőjű golyó 0,5236 cm^3 térfogatú.
A nikkel sűrűsége [url=http://hu.wikipedia.org/wiki/Nikkel]8,908 g/cm^3[/url].
Ebből a tömeg (m=ρ*V): 4,664 g
Ebből következik, hogy a szükséges munka (E=m*g*h) 0,004664 J.
Na és mennyi munka kell a nikkelgolyócska szobahőmérsékletről (25 °C, 298,15 K), Curie-hőmérsékletére (381,85 °C, 627 K) való felmelegítéséhet?
Q = c * m * deltaT = 0,444 J/g*K * 4,664 g * 627 K = 1298 J
No és mekkora teljesítményű fűtőtest kell ahhoz, hogy ezt a 1298 J-nyi energiát minél rövidebb idő alatt (adjunk 0,1 s-ot) előállítsuk?
P = W/t = 1298 J / 0,1 s = 12980 W
Hm, melyik is a több a 1298 J (a befektetett munka), vagy 0,004664 J (kvázi kinyerhető munka)? Számolhatunk a kinyerhető munkához veszteségeket (súrlódás, stb) is - de akkor is nagyságrendekkel nagyobb energiabevitel szükséges.
Quod erat demonstrandum... -
Albertus #544 Szia!
Nos az LCD effektus üzemmeltetése az árammentes vezérlésével, valóban energia mentes lenne.. ne téveszd össze az LCD kijelzők fogyasztásával.
A példában emlegetett kerék miért nem működhetne??
Nos, a helyes válasz, mert a jobb oldalon a felső és alsó helyzet közötti h magasságon (E=m*g*h) kevesebb munkát végez a gravitáció
a három tömegen, mint amennyi kellene ugyanezen h magasságra való felemeléshez a bal oldali tömegekhez..
A példa jól szemlélteti, hogy az erő nem az egyetlen szempont.
A mágneses-Curie fémes megoldás szerinted sokkal több külső energiát igényel mint amennyit termelhetne..
Majdnem igazad van. Ha arra gondolunk, hogy nagyon kevés hőenergiához-látványosan sok mechanikai munka tartozik..
Ha viszont arra gondolunk, hogy a rendszer a golyóval-mágnessel
tulajdonképpen egy mágnese-gravitációs erőmű lenne, akkor ajánlom
figyelmedbe a szélvitorlások azon változatait, amikor a
vonóerőt a széllel szembeni irányba fejtik ki..
(Nem úgy mint a régi, klasszikus vitorlások, cikk-cakkban haladnak a széllel szembe, hanem pontosan szembe..)
A mágneses-gravitációs, de akár (nap-)hő erőművek készítéséhez
a szembevitorlákhoz hasonlóan, meg lehet találni a helyes elrendezést..
A tagadást megmagyarázhatjuk, de attól még senki sem jut előre.. -
 #543
#543
Vagy egy masik pelda mikor az elsullyedt harangban mondjuk egetnenek valamit ami gaznemu egetermeket produkal de ez mar uzemanyagos megoldas es nem tul kornyezetbarat -
 #542
#542
Volt mar itt tema a vizbontas buvarharangban tenger alatt.
Ehhez hasonlo mikor levegot pumpallunk egy buvarharangba ami kb. 100m melyen van.
Tegyuk fel hogy a terfogata mondjuk 1m3. Arra lennek kivancsi hogy mikor elindul felfele mennyi munkat vegez es mikor fent kiengedik belole a levegot es sullyedni kezd akkor mennyi munkat vegez. Es ez a munka eleg e ahhoz hogy a lesullyedt harangot megint telepumpaljak levegolvel. De ez tul egyszerunek tunik hogy mukodjon mert akkor mar mindenki ezt csinalna :)
-
 #541
#541
Igen ám, csak a Finsrud féle kütyü magától le is áll (the machine does stop on occasions), és mivel leáll nem 100% hatásfokú (the machine does stop this means it is not over 100% efficient."). Mivel nem 100% feletti hatásfokú, nem örökmozgó (annak ellenére, hogy sokáig mozog).
A mágnesgolyós Curie-ötvözetes golyós megoldásnál a külső energiabevitel nagyobb (mert kapcsolgatni kell, és a kapcsolgatásra fordított energia összeadódik) mint a golyó mozgása által "nyújtott" energia. -
HUmanEmber41st #540 Orfireus kereke is külső erőbehatásra indult. Aztán mikor elérte ( magától) az üzemi fordulatot, forgatónyomatékot lehetett belőle kinyerni, és csak nagynehezen lehetett megállítani. Tehát az elméleti örökmozgók összerakástól még nem indulnak be, csak külső erőhatásra. Ekkor az erőhatást a rendszer "megőrzi" és míg az anyag el nem kopik-fárad addig mozog. -
 #539
#539
"LCD-khez hasonlóan, pusztán térerősséggel
energia felhasználás nélkül átbillenthető mágneseket készítenek."
Az LCD-hez kell energia.
A pusztán térerősséghez is.
"A Curie ötvözetes megoldásnál pedig, valóban az átbillenés közeli hőmérsékleten kell tartani az egész rendszert. Ez kivitelezési kérdés."
A gyakorlati életben mindent túlméreteznek - a biztos/biztonságos működés miatt. Számítani kell a véletlenre is.
" Kedvenc példám az, hogy ha a kőbaltás ember fia nem készít íjjat,
akkor még ma is a kőbalta lenne a technika csúcsa."
Egy technika, technológia kifejlesztéséhez meg kell lennie a szükséges szociális, tudományos, technikai háttérnek is. Tehát Leonardo nem tudott volna repülőgépet fabrikálni, mert még nem ismerhette azokat a dolgokat, amelyek egy repülőgép kifejlesztéséhez szükségesek. A természet különböző (madarak, repülő növényi részek) jelenségeit megfigyelhette, ezekből elképzeléseket kreálhatott, de gyakorlati megvalósításra nem kerülhetett sor, hisz nem álltak számára az 1800-as években lassanként felfedezett dolgok.
"Amiért említettem az az, hogy ránéztéből "lehetetlen" is megoldható,"
Nem oldható meg, mert nagymértékű energiabevitel (külső) szükséges. -
Albertus #538 Szia!
Igazából símán elnézhetem én is.. mint bárki más is.
Amiért a megoldás egy lehetőségét felvetettem az az, hogy felhívjalak benneteket a kreatív gondolkodásra.
Mert szerintem, majdnem minden lehetséges.. még ha éppen most a
tudásunk szerint lehetetlennek is látszik..
Kedvenc példám az, hogy ha a kőbaltás ember fia nem készít íjjat,
akkor még ma is a kőbalta lenne a technika csúcsa. -
Albertus #537 Szia!
Nos, igaz. Nehéz teljes képet látni. Túl sok ismeretlen rendeltetésű alkatrész van benne..
A Curie ötvözetes megoldásnál pedig, valóban az átbillenés közeli hőmérsékleten kell tartani az egész rendszert. Ez kivitelezési kérdés.
Amiért említettem az az, hogy ránéztéből "lehetetlen" is megoldható,
ha megfelelő feltételeket teremtünk.
Annak idején elképzelhetetlen volt olyan anyag amely elveszti mágneses tulajdonságait. Ma pedig már olyan fejlesztésről is olvashatunk, hogy az LCD-khez hasonlóan, pusztán térerősséggel
energia felhasználás nélkül átbillenthető mágneseket készítenek. -
Locutos #536 Ja és így már értem a hétszeresen meghosszabodó karokat. Igen így lehet van benne lehetõség.
Hogy is gondolhattam hogy Albertus ilyen egyszerût elnézzen! :) -
Locutos #535 Es Faustus te milyen módszert javasolnál a smot effektus kihasználására?(mondjuk tételezzük fel hogy próbálkozni akarnál) -
 #534
#534
"A lényeg az, hogy a munkavégzés nagyságától függetlenűl, annál
sokkal-több nagyságrenddel kevesebb- energiát igényel az átbillentés."
A lényeg az, hogy ahhoz hogy ez az átbillenés meglegyen, kívülről kell energiát bevinni (például lézerrel, mikrohullámmal, sima infralámpával, lánggal vagy a B lyuk körül izzószállal). És ennek a bevitt energiának mindaddig ki kell tartania, míg a golyóbis a B lyuktól az F vályúig gurul lefelé (vagyis több energiát kell bevinni, hisz azonnyomban fel kell hevíteni Curie hőmérséklet fölé a golyóbist annyira, hogy pont az F vályúig tartson ki).
Mikor eléri az F vályút pont akkor kéne visszabillenie (fontos a pontos időzítés), tehát elővigyázatosságból (mert nem biztos hogy kihűl rendesen) az F vályút lehet hogy hűteni kell (a hűtés megoldása energiát emészt fel).
Ja és ha ezt automatizálni akarjuk (mert nem bízhatunk semmit a véletlenre), figyelni kell a mozgó golyóbis hőmérsékletét, és az által kell szabályozni a fűtést. Vagy légkondícionált teremben kell végezni az egészet. -
Locutos #533 Sajnos a norvég csávó kütyüje túlságosan sok beleköthetõ karocskákat, lengõcskéket tartalmaz, meg egy bazi nagy rugót a tetején...ígyhát lehet hogy az aminek látszik, lehet hogy nem az(de simán lehetne az is). De a lényeg az elv. Nem biztos hogy a Billy Meyer motor pont pont a smot modszert alkalmazza, lehet valami hasonlót, de a fõ, hogy ha az a golyócska felfele ment a lejtõn, akkor görbe pályára is megoldható lehet a dolog.(->menjen körbe-körbe)
Na szóval én is említettem, és másoktól is visszaolvastam, nem az energiamegmaradást kell döntögetni...eseteket kell lelni amikor... -
Albertus #532 Szia!
Nem a fokon van a lényeg, bár lehet celziusz is.. Hanem az elven..
A mágnes csak az Curie-hűmérséklet alatti hőmérsékleten vonzza a fémeket.. Amint átlépjük akár milyen piciny értékkel felfelé ezt a hőmérsékletet a mágnes nem vonzza többé.. és beleesik a B pontnál a lyukba..
Különféle hőmérséklettel rendelkező Curie-ötvözeteket gyártanak..
a Welller pákámban pl. 200 C fokos van, de létezik 30 ill. 70 C fokon
"átbillenű" ötvözet is.
A lényeg az, hogy a munkavégzés nagyságától függetlenűl, annál
sokkal-több nagyságrenddel kevesebb- energiát igényel az átbillentés.
Így akár a leeső golyó mozgási energiájának egy parányi részét is felhasználhatjuk erre a célra.
Amiért említettem, az az, hogy ez is jó példa arra, hogy valamikor,
valamilyen kezdetleges tudás (technikai) szinten megvalósíthatatlan
eszközt mint véres kardot hordozzuk körbe, hogy:
"lám-lám nincs működőképes perpetum mobile" pedig van.. több féle is van.. -
 #531
#531
Az alábbi könyv-fejezetben el van magyarázva miért nem működhet.
Lukács Ernőné, Péter Ágnes, Tarján Rezsőné - Tarkabarka fizika, Móra Ferenc könyvkiadó 1972 82-83. oldal: Mágneses örökmozgó
Az általad említett "fűtéshez" pedig egyrészt külső energiabevitel szükséges, másrészt a "0,000 001 fok" (Milyen fok? Celsius? Kelvin? Réaumur? Fahrenheit? Radián?) olyan kicsi, hogy azt a hőfokstabilitást nehezen tudod biztosítani.
De játsszunk el a gondolattal - a fenti mágnesgolyó helyére rakjunk elektromágnest, aminek a mágnesességét remekül tudjuk szabályozni.
Bár külső energiabevitel kell, de azzal talán megoldható lenne a játék. -
 #530
#530
"Node kérem! Honan veszed?"
Onnan, hogy a készítő (Reidar Finsrud) kijelentette, hogy a gép 1. alkalmanként leáll 2. az ingákat külső energiabevitellel lengetik be.
Ezekből következik, hogy nem perpetuum mobile, csak egy jó sokáig mozgó szerkezet.
" Különben is, ha jobban megfigyeled a mozgást indítási energiaszint zéró, aminél bármennyi is több.."
Zéró egy fülesbaglyot! Az ingákat kézzel lengetik be - azaz az indítási energiaszint nem zéró.
"A filmek nem tünnek hamisítványnak."
A smot mint mondtam az asszimmetrikus mágneses mező révén működik (mivel kézzel emelik a golyót nem perpetuum mobile).
A Finsrud-féle ketyere, az előzőekben volt tárgyalva (ugyancsak nem örökmozgó).
Az [url=http://www.youtube.com/watch?v=hl8dM2wQB4k&NR]"Orffyreus Perpetuum mobile"[/url]-videó egy klasszikus Villard de Honnecourt-féle kerékhez hasonlót mutat be.
Az ezen a videón látható eszközök szimpla 3d animációk.
A gyertyás áramgenerátorral való átverést ne is említsük. -
Albertus #529 Szia!
Azt írod:
"Nem 100% feletti hatásfok => nem perpetuum mobile. "
Node kérem! Honan veszed?
Különben is, ha jobban megfigyeled a mozgást indítási energiaszint zéró, aminél bármennyi is több..
A gördülési munka.. minden körben újra és újra leküzdi a mágneses tér energiája..
Arról nem is szólva, hogy a Maxwelli butaság szerint a nyugvó mágneses tér nem sugárzódik ki..
Így a fizika jelen állása szerint a semmiből nyeri a golyó
a mozgásához szükséges összes energiát..
Ezért, a jelen hatásfok számítási módszerink szerint sokszorosan
100% feletti a hatásfoka..
-
Albertus #528 Szia!
Sok dolgom volt.. Néha benéztem ugyan, de nem láttam olyat amire ne
feleltetek volna jól, így nem szóltam hozzá.. -
Albertus #527 Arról nem is szólva, hogy itt van pl. ez:
http://www.mszh.hu/kiadv/ipsz/200312/images/06-technika_04.gif
És mi van akkor, ha a golyó Curie a hőmérsékletét a B pontnál eléri,
0,000 001 fokkal átlépi..?
Akkor elveszti a "mágnesességét" és működik, vagyis valóban beleesik a lyukba, lehüli azt a 0,000 001 fok pluszt amire allúra ér és ismét vonzza a mágnes, majd ismét 0,000 001 fokkal felmelegszik amire felér a lyukhoz..
Ha még a forgási örvényáramok melegítő hatását figyelembe is veszem..
külső meklegítő forrásra sincs szükség, mégis "örökmozgó"..
Viszont bambaagyú műokosok kijelentették róla, hogy nem is lehet
olyan, hogy működik, mert "" "perpetum mobile" és azt ugye tudjuk, hogy
nem lehetséges..""
Különben a mágneses, nagyon tetszik..