Matematika feladatok
-
 #524
#524
Én mérnöki szemmel rögvest valami ilyesmit csinálnék: Van két stratégiám:
1.) Maradjunk minél messzebb a kannibál bácsitól és úgy ússzunk
2.) Igyekezzünk úgy kiúszni, hogy úgy érjek partot, hogy a kannibál és én végtelenül kis távolságra legyünk egymástól legalább, hogy a parton már elspurizhassak előle
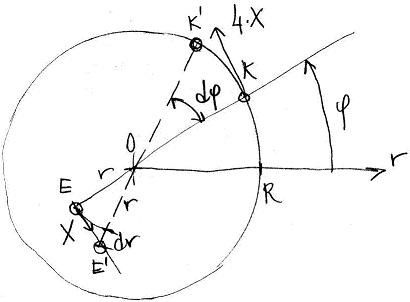
Az első esetet ezen az ábrán lehet látni:
Úgy indul a dolog, hogy a kannibállal (K) ellentétes irányba indul el az emberünk (E). Elemi kis idő alatt K d_fi szöget mozdul el a parton, tehát megtesz R*d_fi utat úgy, hogy igaz R*d_fi/d_t=4*X, merthogy ekkora a sebessége.
Az úszós fickó ezalatt szintén d_fi -t úszik érintőirányba (mert szeretne minél messzebb maradni) és ha még belefér az X sebességbe, akkor a part felé is szeretne d_r -t. Azaz az ő esetében a sebesség úgy néz ki, hogy NÉGYZETGYÖK((r*d_fi)^2+d_r^2)/d_t=X
Namost némi átrendezgetés árárn azt kapjuk ebből a két egyenletből, hogy d_r=NÉGYZETGYÖK((R*d_fi)^2/16-(r*d_fi)^2).
És ez a gyökvonás akkor lehetséges, ha r<=R/4, azaz az 1.) stratégiával a fenti sebességviszonyok esetén csak a tó sugarának negyedéig tud kiúszni, ezután a kannibál mindíg tud úgy helyezkedni, hogy amíg az úszó a legmesszebb igyekszik tőle úszni, addig ő már megint a rámozdulás előtti helyzetbe ér.
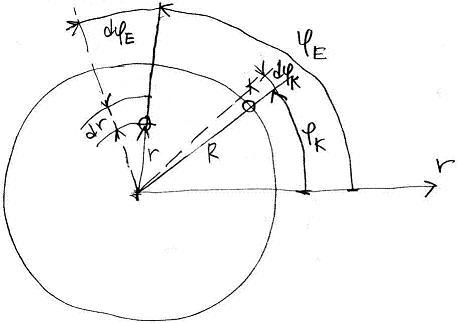
A 2.) stratégiának az a lényege, hogy K-nak és E-nek szabadon változhat d_t idő alatt a szögelfordulása, emiatt megvalósítható(??? ezt még nem írogattam le ???) az az eset, hogy amikor az úszó ember r-je egyenlő R-rel (azaz kiért a partra), akkor a fi_K = fi_E, azaz ugyanott vannak. És akkor illa berek náda kerek 4X+1 -el futás (persze ez a határhelyzet, de ezt kell vizslatni).
Itt van hozzá a hasonló ábra:
Ezt még lehet bogarászni kicsit, az viszont már most nyilvánvaló, hogy kell egy célfüggvény, amit az úszó meg akar valósítani azon kívül, hogy r:=R és hogy fi_E>=fi_K. Mert így nagyon sok megoldás szóba jöhet. Az is jó módszer, hogy a pálya érintőjét állítjuk elő időlépésenként!!! A kezdeti derivált eléggé nyilvánvaló: minél messzebb a gaz K-tól, azaz legyen +végtelen (90fok).
Ennyi egyelőre - remélem a numerikus matekosok ettől beindulnak!
-=ZR=-