4415
Matematika feladatok
-
#1932
3-(a/2)
? -
 #1931
#1931
hát én is furcsáltam.. mert matekos vagyok am.. és nem vágtam elsőre.. de elvileg a gyereknek csak ennyit diktált a tanár..:D:D -
ba32107 #1930 Ömmm.....és mi a szart csináljunk vele? Nem hagytad le az egyenlet másik felét? 
-
 #1929
#1929
tehát azt szerettem volna írni, hogy valaki meg tudná csinálni nekem..?:D -
 #1928
#1928
hello vok ezt emgtudná csinálni?? 1/2*(6-a)
köszi!! -
ba32107 #1927 Wikipedia -
 #1926
#1926
Hi egyszerűen fogalmazva meg tudna vki mondani mi az hogy:
-küszöbszám
-konvergens egy sorozat
-határérték -
 #1925
#1925
milyen háromszög?
én abból indiltam ki, hogy egy kör megszerkesztéséhez 3 pont kell.
persze tekinthetjük az általuk kijelölt háromszög köré írt körnek is, de ennek nincs túl nagy lelentősége.
már csak azért sem, mert igazad van, meg kell vizsgálni minden két pontra, mint átmérőre illeszkedő kört is.
ez 10*9=90db -al több kör mint amit korábban írtam.
de ezzel a kiegészítéssel már jó az elméletem? -
supercharley #1924 Ez esetben nincs háromszög ...
[IMG][/IMG]
-
 #1923
#1923
ha ez a feladat, hát ez a feladat.
(én nem teljesen értem, hogy mire jó annak a körnek a sugara, mert az eloszlást szerintem nem jellemzi eléggé, de ha ez kell, hát ez kell.)
ha viszont tényleg fix 10 lövés van, akkor továbbra is a "minden kört kiszámítok" módszert találom a legolcsóbbnak (leggyorsabbnak).
mégegyszer, mennyi számítás is?
10*9*8=720db kört határoznak meg a pontok hármas csoportjai.
(1db (for) ciklus i=1..720)
minden körről el kell dönteni, hogy benne van-e az összes pont.
ez akkora maradék 7 pontra 720*7=5040 számítás. (nagyobb-e a pont távolsága a vizsgált kör középpontjától, mint a sugar?)
(1db (for) ciklus i=1..5040)
és a jó körök közül a legkisebb sugarú. (ami egy feltételvizsgálat és egy értékadás)
ez 720+5040=5760 számítás, és két ciklus, néháy (kb 3) feltétel vizsgálat.
a két ciklus ráadásul egymásba is ágyazható.
egy mai átlag pc-n a futási idő (hasamraütök) kevesebb mint 1 másodperc (tippem: kevesebb mint 0,1 másodperc).
és tutipontos, mindig jó.
-
 #1922
#1922
... francba:
...majd a kört úgy rajzolom meg, h melyik találat esik legtávolabb a súlyponthoz... -
 #1921
#1921
... jut eszembe: félreértettem a dolgot: tehát nem arról van szó, hogy egy hüvelyből több lőszer repül ki egyszerre és vizsgálják, mennyire szóródik szét, hanem több lövést leadva mennyire...
Ebben az esetben a súlypontos nem jó módszer... Ellenben kezdő adattal szolgál egy másik algoritmusnak - mondjuk a középpont az maradhat de a sugarat 1-2%-kal érdemes megnövelni és onnan futtatni a "pontosabb" algoritmust.
Elég macerás lehet ezt kézzel csinálni, nem...?! -
 #1920
#1920
Ha megkeresem a súlypontot, majd a kört úgy rajzolom meg, h melyik találat esik legközelebb a súlyponthoz, a következőt kapom (elég pontos a szerkesztés, egy kis AutoCAD van mögötte - tehát nem a pontatlanság miatt "van mellette" a másik körnek):
-
supercharley #1919 A konkrét feldat továbbra is a következő:
Lőtéren tesztelnek lőszert, és annak a szóráskép vizsgálatához kell
ezt a legkisebb kört meghatározni. A lövések száma mindig 10.
A lőlap szkenelve, képernyőn egérrel kijelölve a 10 lövés,
így megkapjuk azok koordinátáit. Ezen 10 koordináta alapján lehet
kiszámolni a legkisebb köréjük írható kör origóját és sugarát,
bár igazából az átmérőre van szükség, de úgy szép a megoldás ha már
be is rajzoljuk azt.
-
 #1918
#1918
kiszámolhatnánk annak a valószínűségét is, hogy miki egeret formáznak a becsapódások, de télleg tudni kéne, hogy mi a feladat. -
 #1917
#1917
Pl.: lehet rápakolni 2D-s normális eloszlást:
A súlypont x, y lesz a várható érték helye és a szórás a 2 irányba számolható (utána kell járni, hogy "klasszikus módon", vagy van benne vmi trükk, mert 2D - de nem gondolnám...) -
 #1916
#1916
hát ez igaz, most má télleg csak azt kéne tudnunk, hogy mi is a konkrét feladat. -
 #1915
#1915
nos akkor:
1.) Súlypontot kiszámol
2.) Súlyponttól vett távolságokat kiszámol, ez lesz 10 db távolság
3.) A 2. pont alatt kiszámolt távolságok közül a legnagyobb egy jó közelítése a keresett sugárnak
A fenti módszer nagyon egyszerű és legalább olyan hasznos, mint a legkisebb burkolókör, már csak azért is, mert ahogy tudjuk kinematika-dinamikából: egy anyagi pontrendszer úgy mozog, mintha egy pontból állna, ez a pont a rendszer súlypontja. Ha a test több darabból áll, a súlypont a súlypont eredeti pályáján halad tovább, annak ellenére, hogy a rendszer részei e pályától egyre távolodnak. -
 #1914
#1914
mi a teljes feladat? -
 #1913
#1913
hátőőőő....
statisztikából vannak olyan módszerek, amik lehet, hogy sokkal jobban modellezik ezt a dolgot. -
supercharley #1912 Aha, látom hogy létezett már ilyen versenyfeladat. Érdekes, mert ez meg konkrétan egy munkahelyi feladat megvalósítása lenne. Lőtéren tesztelnek lőszert, és annak a szóráskép vizsgálatához kell ezt a legkisebb kört meghatározni. -
 #1911
#1911
de ha tudjuk, hogy csk kb 10 pontunk van, akkor viszonylag gyorsan legyárthatnánk a konvex burkoló sokszögét (vagy hogy is hívják aszt a ráfeszülő izét), ami ha 3szög, akkor nyertünk, ha nem akkor is (általában) kevesebb pont marad, mint eredetileg.
a burkolókörhöz ezek közül 3 kell, vagyis rajzoljuk fel az összes lehetséges kört.
ha mégiscsak 10 pontunk maradt, akkor 10*9*8=720 körünk van.
ezek kötül (legalább) egy nyerő.
hogy melyik? hát azok közül, amelyikekből nem lóg ki egy pont sem, na azok közül a legkisebb.
persze ez a vége csak egyszerűnek hangzik... de... hát végülis nem olyan bonyolult.
minen körhöz megnézzük a maradék (max) 7 pont távolságát, ami 720*7=5040.
nem olyan rossz ez, megvan sitty-sutty. -
 #1910
#1910


 Még nem írtam meg...
Még nem írtam meg...
kz: igen, az vele a gond, h sokáig fut, főleg amikor már belőtte körülbelül a középpont helyét és a sugarat és csak finomítja -
 #1909
#1909
az implementációhoz is van segítség itt.
-
 #1908
#1908
nem rossz ötlet, bár nem vagyok benne biztos, hogy hatékonyabb lesz, mármint ordóilag. -
supercharley #1907 Hurrá, egy program jól jönne, ha lehet C#-ban. -
 #1906
#1906
sokkal egyszerűbb egy jó nagy körrel indítani, ami Brown-mozgást végez és közben szűkül, miközben betartja azt a szabályt, hogy annál kisebb valószínűséggel fog a kör a körvonalhoz legközelebb levő pont irányába lépni, minél kisebb a távolság a pont és a körvonal között.
Ez nagyon könnyen programozható és meg is írom - ha már nem a melóhelyen leszek... :P -
supercharley #1905 Értjük a megoldást, de a leprogramozással gondok lesznek, ha más nem hát a kreskítések miatt. -
supercharley #1904 Programot kellene írni rá. -
 #1903
#1903
lehet, hogy ez a Balázs gyerek se olyan jó matekból, csak angolból és innen nyúlta az egészet?
nemtom, nem hiszem... -
 #1902
#1902
programot kell írnod, vagy elég az előző lírás (algoritmus)? -
 #1901
#1901
na ez má csak jó....
A megoldás Kezes Balázs érsekújvári diák munkája.
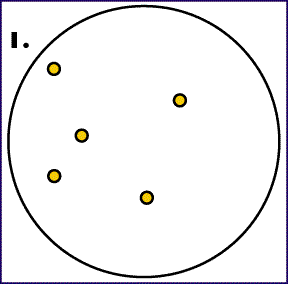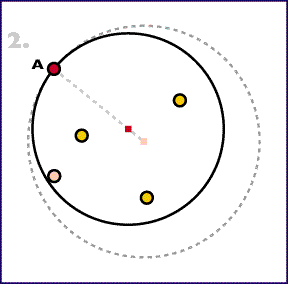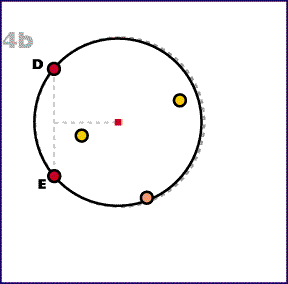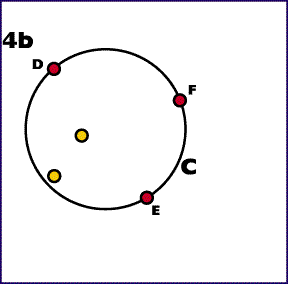
1. Rajzoljunk meg egy kört az összes pont körül. Nyilvánvaló, hogy ezt lehet kisebbíteni.
2. Kisebbítsük a kört az olyan A pont megkeresésével, amely a legtávolabb van a középponttól, és rajzoljuk egy új kört ugyanazzal a középponttal és a körvonala haladjon át az A ponton. Ezzel létrehoztunk egy kisebb kört, amelyben szintén benne van az összes pont, de most áthalad az A ponton ahelyett, hogy körülötte lenne.
3. Ha a kör áthalad 2 vagy több ponton, akkor ugorjunk a 4. lépéshez. Ellenkező esetben kisebbítsük a kört a kör közepének az A pont felé valő tolásával, amíg nem érint egy másik B pontot a többi pontból.
4. Ennél a pontnál már van egy körünk, ami kettő vagy több ponton már áthalad. Ha a kör körvonala tartalmaz, egy olyan körív intervallumot, amely nagyobb mint a kör kerületének a fele, és semmilyen pont nem tartózkodik rajta, akkor a kört lehet kisebbíteni. Az ilyen intervallumot pont-mentes intervallumnak fogjuk nevezni. Legyenek a D és E pontok ezen a pont-mentes intervallum végein. Miközben a D és E pontokat a körvonalon tartjuk, kisebbítsük a kör átmérőjét amíg a. az átmérő távolsága nem |DE|, vagy b. a kör körvonala nem érint egy harmadik F pontot.
Az a. esetben végeztünk. A b. esetben meg kell vizsgálnunk, hogy van-e a kerület felénél nagyobb pont-mentes intervallum. Ha nincs, akkor végeztünk. Ellenkező esetben meg a három pontnak egy olyan köríven kell feküdnie, amely rövidebb mint a kerület fele. Meg kell ismételnünk a 4. lépést a két külső ponttal.
Az első három lépés lineárisan függ a pontok mennyisségétől. A 4. lépésben minden új F pont megtalálása is lineárisan függ a pontok mennyisségétől. De az F pont megtalálása nem garantálja az algoritmus végét, és az addig ismétlődik, amíg van pont-mentes intervallum, melynek nagysága nagyobb mint a kerületnek a fele. Legfeljebb (n-2)-ször kell ismételni a 4. lépést, ami O(n2) időbonyolultságot eredményez.
-
 #1900
#1900
hát még ez is kevés.
akkor őőő....
ez már segít? -
supercharley #1899 Nem jó egyik sem. Ezeket már próbáltam egy egyszerű rajzokon ellenőrizhető hogy így nem ok. -
 #1898
#1898
első ötletem: a ét legtávolabbit összekötő szakasz legyen az átlója a körnek.
de ez mintha nem lenne tuti.
legyen a három legtávolabbi és az általuk kijelölt háromszög köré írható kör.
vagy valami ilyesmi:) -
supercharley #1897 Sziasztok!
Sajnos én kevéssé értek a matekhoz, de van egy olyan feladatom amit mégis meg kellene oldanom. Arról van szó, hogy adott egy adott területen
vannak szétszórva pontok, amiknek tudom a koordinátáit(általában 10 pont). Meg kellene határoznom a köréjük írható legkisebb kört. Tehát tudnom kellene a kör középpontját, és a sugarát. Ötletem éppen van, de nem vagyok biztos benne hogy az általam megtalált kör biztosan a legkisebb. Tud ebben valaki segíteni? -
lally #1896 Igazat adok mr."ZilogR"-Processzor úrnak !
-bááár,
a szüzike-olajjal *felkent Bolonyéze*-maszlaggal, most; Pöttyet alaposan betettek a mérnökeinknek !!!
-hisz', ha mindenki számára: Triviális az, hogy csak egy gyakorló orvos tudja meghatározni azt; Milyen tárgyai is legyenek okvetlen, e doki-palántáknak;
Mérnökeinknél, Miért is suta-közgazda uraink döntik ezt itt el ?!
-
pista007 #1895 Nagyon szépen köszönöm! Lehet, hogy tanulok ebből az esetből, és megfogadom a tanácsodat 
-
ba32107 #1894 

-
 #1893
#1893
na, nézzük az én esetemet:
Én akkor tájban kezdtem az alkalmazott matematikus-on gondolkodni, amikor a BME TTK is elkezdte a ténykedését. Akkor 30 főt vettek fel és volt 6 szakirányuk. Évente kb 15-20-an jelentkeztek oda. Annyit kell tudni a szakirányválasztásról, hogy ha 6-nál kevesebben jelentkeznek egy szakirányra, akkor az nem indul, akik oda jelentkeztek, azok kénytelenek más induló szakirányt keresni.
Voltam a nyílt napon és ezt megkérdeztem a TTK dékánjától is, (konkrétan azt, h "Önök maximum 30 embert vesznek fel és van 6 szakirányuk, mi van, ha az én szakirányom nem fog elindulni, pedig 3 évet áldozok arra, hogy el jussak a szakirány választásig?", amire ő szó szerint azt mondta, h "Akkor pechje van!" és még nevetgélt is...
Ekkor rögtön tudtam, h ebből semmi jó nem sülhet ki így mentem azonnal a gépészkarra és állíthatom, nem volt rossz a választás! Rengeteg szakirány, mindegyikre sok jelentkező és még matematikus is lehetsz, mert a gépészkaron az is van! De én biztosra mondom, h nem fogsz semmi effélét választani, annyira hatalmas kihívások vannak a többi szakirányokon (pl. mechanika és áramlástan)
Az a legjobb, hogy műszaki szemléletet ad és nem leszel semmihez sem értő "kocka" hatalmas elméleti tudással a fejedben, hanem leszel egy mérnök, hatalmas elméleti tudással a fejedben, hatalmas gyakorlati érzékkel és tapasztalattal és érteni fogsz rengeteg gyakorlati dologhoz!
Hogy mivel foglalkozol mint matematikus? Bármivel - ha van hozzá érzéked! Mint mérnök szintúgy! Én gépész vagyok és néhány hónap rágyúrás után programot írok neked Symbian alá, ha nagyon kell. :P De most éppen erőművekbe tervezek pernyeszállító berendezéseket, úgy, hogy utolsó csavarig - és az a szép, hogy meg is építik, odaszállítják és beüzemelik - több millió eurós projektek!
Jó vagy matekból? Értesz a programozáshoz? És még a pénzügy is érdekel? Akkor talán foglalkozhatsz olyan szoftverek írásával, amik tőzsdén adnak vesznek részvényeket. Voltak ilyen cégek, matematikusok és fizikusok szoktak efféléket alapítani - ha jól megy, akkor a bankok általában felvásárolják őket :P (pl.: Prediction Company, láttam velük egy dokumentumfilmet, a cégük előcsarnokában volt egy hatalmas kijelző, ami a cég vagyonát mutatta - elmentek ebédelni és mikor visszajöttek, ez egyik odaállt elé és viccesen megjegyezte, h "Nocsak, megint kerestünk egy milliót..."). Ha két évre 1% pontossággal tudnád előre jelezni a magyar gazdaság GDP-jét, bármennyit kérhetsz... :P
Túrjad a különböző karok weboldalait, mert rengeteg dolog fenn van!
 [/IMG]
[/IMG]