4415
Matematika feladatok
-
bszabolcs21 #2012 A lényeg az, hogy van egy járattervező program amely szerint:
1 tipus: 1 db
2 tipus: 5 db
3 tipus: 11 db
és meg kellene "kézi módszerrel" is határozni a szükséges járművek számát. -
ba32107 #2011 Nem értem, hogy jönnek ide a vevők, alapban kicsit értelmetlen a feladat. Úgy több értelme lenne, ha mondjuk az autókhoz rendelnénk költségeket, és minimalizálni kéne azt. De amúgy egy lehetséges megoldás:
40 darab 3. típusú: 800
2 db 2. típusú: 832
1 db 1. típusú: 844 -
bszabolcs21 #2010 még annyit, hogy gondolom valamilyen súlyozással kell megoldani -
bszabolcs21 #2009 Hali!
Lenne egy feladat amelyben kellene egy kis segítség:
Adott 839 raklap. Ezt a mennyiséget 3 fajta teherbírású autóval kell elszállítani.
1. típus: 12 raklap fér fel
2. típus: 16 raklap fér fel
3. típus: 20 raklap fér fel
103 vevőnk van, 1 vevő átlagos igénye: 839/103=8,15 raklap
Kérdés: Hány autóra van szükségünk típusonként, ha mind3 autót használjuk? -
Dzsez #2008 Talán nem az a jó megoldás ami a CD-n van? -
lally #2007 ... Üdv Néked Slapi19 !
- azér', annyira má'; Ne nagyon degradáljuk le most itt; A matek-okításunkat!
(hisz: 10félévnyi egyetemi-, +1 gyakorlati-év esetén is =
= Szumma 6 évvel kellene számolnunk. - tehát:)
Annó, volt akkor még, egy matek-felvételi is !
- ahol, a *Zöld-könyv* #2357. példája; Egy *jó-közepesnek* számított csak.
(... mérnöki szemmel (nézve) pedig, a; *KÚP*, mint fogalom. -szavunk, ...
... Rátok bízom !)
-
 #2006
#2006
mondjuk hamatek tanár, elég gáz ha egy ilyen feladatot nem tudott megoldani, főleg úgy hogy rajt van megoldás cd-n:) -
Slapi19 #2005 Köszi a válaszokat rengheteg segítség volt a számomra. Csak azért írtam hogy egyetemi végzettsége van, mert van főiskolai végzettségű tanár is ami egy kisebb fokú végzettség, nem tud annyit mint egy egyetemi tanár. Ez hihetetlen 3 napja ezen az egy példán ülök és mindent elő vettem és így sem sikerült megcsinálni, pedig az osztályomhoz képest jó vagyok matekból, de ez kifogott rajtam. Mégegyszer köszi!
-
ba32107 #2004 Mondjuk ha matektanár, elég valószínű, hogy egyetemi végzettsége van... -
 #2003
#2003
nem tudta megoldani, pedig matek tanár?
vagy csak egyetemi végzettsége van?
végülis mindegy, figyelj az órákon, sokat tanulhatsz tőle... -
 #2002
#2002
ték -
köny #2001 Köszi -
ba32107 #2000 a. 0C
b. -1C
c. 7C
ja és TÉK -
köny #1999 Melyki az a hömérsékleti érték, amely
a, ugyanannyival melegebb a -7C-nál, mint amennyivel hidegebb a 7C-nál?
b, ugyanannyival melegebb a -8C-nál, mint amennyivel hidegebb a 6C-nál?
c, ugyanannyival melegebb a -5C-nál, mint amennyivel hidegebb a 19C-nál? -
Thibi #1998 picit máshogy indulva egyszerűbb egyenlet jön ki:
r*m=209 ebből m=209/r
r^2+r*R*pi=1978.11 ebből R=(1978.11/(pi*r)-r
r^2+m^2=R^2 ebbe behelyettesítve az m és R értékét
r^2=((209^2-(1978.11/3.14)^2)/(-2*1978.11/3.14))
r=16.74266 -
pet0330 #1997 Szia!
Elvileg megvan.
A=pi*r·2+pi*r*gyök(r·2+m·2)=1978.11
T=d*m/2=2r*m/2=r*m=209
m=209/r
Ha m helyére behelyettesítek:
pi*r·2+pi*r*gyök(r·2+(43681/r·2))=1978.11
Ezt r-re megoldva(csak programmal tudtam) kb.16.75cm-t kapsz.
Ebből pedig h 12.4776cm. -
gotchaaa #1996 Zöld összefoglaló feladatgyűjtemény 2357.? Szép feladat. :) -
Slapi19 #1995 Sziasztok! Van egy feladat amit a matek tanárom sem tudott megcsinálni, pedig egyetemi végzettsége van. Egyszerűnek tűnik, mégis nehéz! A feladat így szól: "Egy egyenes forgáskúp felszine 1978,11 cm2, tengelymetszetének területe 209cm2. Mennyi a kúp térfogata?". Ennyi az egész feladat több adat nincs megadva. Ha valaki tudna nekem erre a feladatra választ adni vagy valami kiindulópontot azt nagyon megköszönném. A válaszokat előre is köszi! -
lally #1994 Okay, mertem is remélni a +75 eredményed!
(-de: 2. sor szerinti kifejtést szokták kérni, egy fogósabb ZH-példában;
tehát erre is oldjátok most meg ! -ha javasolhatom.)
Ám, ha Cramer-szabályt is kell majd alkalmaznotok,
fölényesen a leggyorsabb módszer, amit #1992-ben leírtam.
-
ba32107 #1993 A te módszeredet egyáltalán nem értem. Én úgy szoktam, hogy Gauss eliminációval felső háromszög-mátrix alakra hozom, onnan meg már egyszerű. A kifejtési tétel számomra bonyolultabb. De azt nem is értem, hogy most mit csináltál, mert nem úgy tűnik, hogy kifejtetted.
Amúgy nekem is 75 jött ki. -
lally #1992 Mate317 és Ba32107 !
Próbálok itt leírni egy kontrollált példát:
4 2 -3
1 5 1
2 7 5 estére.
Először a Főátlói, azaz "\ ,backslash" irányára kifejtve:
Mindez, pozitív alapokkal lesz!
+(4*5*5) + (2*1*2)+ (1*7*(-3))
Mellékátlói: "²/ " iránnyal pedig Negatívak:
-((-3)*5*2) -(2*1*5) -(1*7*4)
Összevont eredménye tehát = +75
Ezt a módszert okvetlen tanuld meg, mert a harmadik példád után,
már biztosan nem is cseszheted el.
-
 #1991
#1991
ny helyett legyen n, az egyszerűbb.
tatai+öveges=versen
vagyis
10000t+1000a+100t+10a+i+100000ö+10000v+1000e+100g+10e+s=100000v+10000e+1000r+100s+10e+n
és
i+s=n, vagy i+s=10+n
mivel a+e=e, vagy a+e+1=e, vagy a+e=10+e, vagy a+e+1=10+e.
azaz vagy a=0, vagy a=-1, vagy a=10, vagy a=9, ebből a középső kettő kizárható, mivel 0<=a<=9
és így tovább a többire.
remélem így már menni fog! -
 #1990
#1990
Hi!
Tudnátok megoldást nekem az #1971-es feladatra?
Itt egy kép, hogyan is néz ki a példa(az ide leírt összeadás kicsit félresikeredett..)
link
Előre is köszi. -
lally #1989 Szerintem, e jegyzeted írója itt, most egy jó-nagyot bakizott!
(-bár, soha nem voltam egy számtani-géniusz.
-apám szerint Mi, Ott; csak_*számtant* tanultunk.)
Az előjelek *ugrálásai* miatt, a
2.sor szerinti kifejtéssel végezte Ő, amikor (-) előjellel kéne kezdődnie.
(-ezért is szoktuk inkább, csak az elsősorit alapul venni kifejtésre.)
Emlékeim alapján;"Kelemen-szerint", könnyű is megjegyezni, ha indexelsz.
pl.:első-sor,első-oszlopának előjele tehát:
A11 eleme -> (-1)^1+1 = (-1)^2= tehát (+)
de:
2.sori első eleme pedig: A21 -> (-1)^2+1= (-1)^3 =(-)
Bízom benne, most érthető is voltam.
-
ba32107 #1988 Igazából én csak beírtam a mátrixot a programomba, amit régebben írtam, nem számoltam ki kézzel. De bízom benne, hogy a programom helyes :)
Gauss eliminációval dolgozik amúgy (felső háromszög mátrix) -
tivadar89 #1987 Köszi, így már értem. A negatív szám tényleg megzavart. -
mate317 #1986 matrix.pdf
A 10. oldalon a "TIPP!!!" alatt hozza ki -5.re -
 #1985
#1985
a 2.)-es pontnál nem kell zavarba jönni a négyzetgyök miatt, mert egy szám négyzetgyöke nem lehet negatív, így me előjele alapján azonnal fogod tudni, h melyik f(x)-et kell használnod! (Merthogy kettő lesz belőle, egy (+)-os, megy egy (-)-os.) -
lally #1984 Üdv Néked, Ba32107 !
Részletezhetnéd (is) légyszí'; Ezt a :Mínusz_Ötöt ?!
(-hisz': Bő 30éve má, nem kellett fejben, Mátrixot számolnom .
-sőőőt, még az első-sorának kifejtésével is;
+5-re jutottam. -most is!
)
Mate317 !
-ha a: Lineáris algebrai egyenletrendszerekből, a *Cramer-szabály* miatt számoltunk,
Szkennereld be légyszí, e; Tanárod_könyvének, ezen-részletét!
Köszi.
(-mer', a jó papa is holtig akar tanulni.)
-
 #1983
#1983
1.) egyenes egyenletét y=me*x+b alakra rendezed, onnan megvan az egyenesed me meredeksége.
2.) hiperbolát is hasonlóan y=f(x) alakra rendezed
3.) előállítod f'(x)-et
4.) megoldod az f'(x)=me egyenletedet, abból meglesz, melyik pontjaiba húzható a hiperbolának az egyeneseddel párhuzamos érintője
5.) ha megvan az érintési pont x koordinátája, akkor kiszámolod hozzá az y-t és az ismert me meredekséggel az imént kiszámolt x,y ponton átmenő egyenes egyenletét felírod! KÉSZ!
x~2.1357 egy jó megoldás -
tivadar89 #1982 Ebben a feladatban kérnék egy kis segítséget:
Írja fel azoknak az egyeneseknek az egyenletét, melyek érintik az x^2-4y^2=4 egyenletű hiperbolát és párhuzamosak az x-5y+2=0 egyenletű egyenessel.
Eddig jutottam:
-Egyenes meredeksége: m=(x+2)/5
majd kiszámoltam a hiperbola egyenletének a deriváltját: y'=x/4y
A folytatásra nem jöttem rá :S -
masoma #1981 köszi :) -
ba32107 #1980 -5 a helyes válasz. -
mate317 #1979 Nekem is ez jött ki, de a tankönyvben ahol sorbafejtéssel csinálták ott -5, ezt nem értem. -
lally #1978 Üdv, Mate317 !
-picit furán fogalmaztál.
(fő - mellékÁtlósan:) Tehát,: +5
= 1*1*0 +2*1*(-2) + 0*(-3)*3 -3*1*(-2) -(-3)*1*1 -2*0*0 =
=0-4-0+6+3 -0 =+5
s, bízom benne; Nem is csesztem el !
-
mate317 #1977 Hello!
ennek a mátrixnak mennyi a determinánsa? +vagy- 5?
1 2 3
0 1 1
-2 -3 0
-
 #1976
#1976
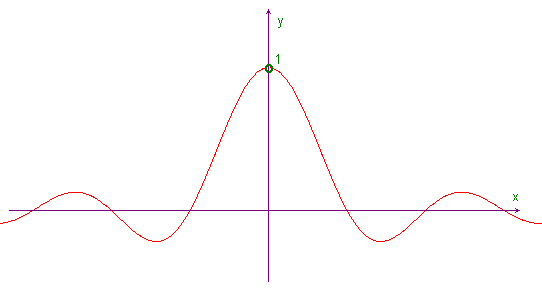
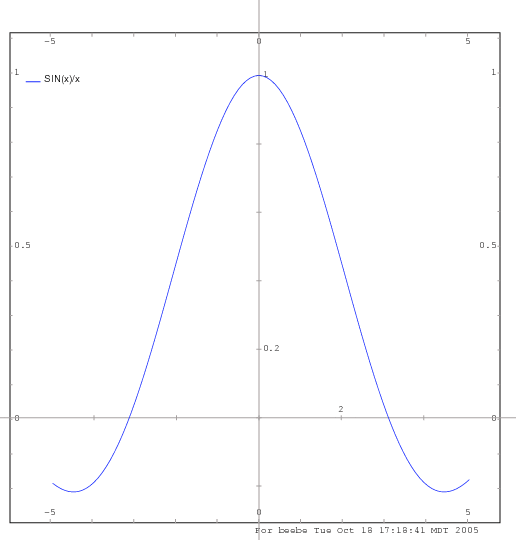
kár, hogy nem sin(x)/n volt a kérdés, azt tudtam volna 
-
ba32107 #1975 -
#1974
igy :C -
masoma #1973 sinx/x függvény hogy néz ki? előre kösz a választ