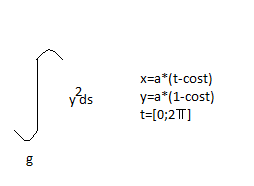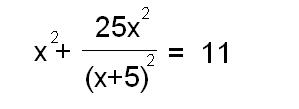4415
Matematika feladatok
-
polarka #4015 wolframalpha -
 #4014
#4014
hali emberek,határértékszámításban kéne egy kis segítség,ha lim n->végtelenbe (n+3/n+1) az n-ediken a feladat,és nem tudom,hogy kéne 1+1/n-é alakítani :) -
Peti95 #4013 Ha az a/b + b/a -t közös nevezőre hozom azt kapom, hogy (a+b)/(a×c)
Az a a+b -t össze tudom vonni de nem tudok előrébb jutni. -
 #4012
#4012
1.) az összeg két tagját felírod valamilyen közös alappal
2.) észreveszed, hogy olyasmit kaptál, hogy a/b + b/a = 2
3.) ezt közös nevezőre
4.) ez ismerős valami lesz
5.) innen meg már könnyű :P -
Peti95 #4011 Ezt hogy kell megoldani?
log·cosX·sinX + log·sinX·cosX = 2
Két · jel közé írtam a logaritmusok alapját. -
polarka #4010 jah és persze ennek az a³-szöröse volna a válasz, ha tényleg azon görbe ívhosszának az y² szerinti súlyozása a kérdés -
polarka #4009 Mármint a paraméteres görbe ívhosszának számítására? enwiki
H analitikusan ki lehet-e hozni, azt most helyből nem mondom meg, mindenesetre a wolframalfa, nem adott meg primitív fv-t, így valszeg nem. De numerikusan adott eredményt. wolframα -
 #4008
#4008
@polarka: koszonom de nekem levezetes is kellene. Tudnad nekem mellekelni? -
polarka #4007 vagy itt -
polarka #4006 ds=sqrt(x.^2+y.^2)dt
eztán már számolható t szerint integrálva
egyébként ez nem ciklois, ahhoz t-sint kéne
online java applet gyors ellenőrzésre -
napstR #4005 Nagyon szépen köszönöm a segítséget! Nem jöttem volna rá :) -
 #4004
#4004
Nos, ha minden igaz, akkor te azt mondod, h úgy lehet megkapni a v2-t, hogy a Z-t átskálázod a 2...10 intervallumra.
Azaz
ha Z=0, akkor v2=2,
ha Z=1, akkor v2=10 és
v2=m*Z+c
A fenti két esetet behelyettesíted az egyenletedbe és megkapod c-t és m-et:
2=m*0+c --> c=2
10=m*1+c=m+2 --> m=8
ezzel kiszámítva v2-ket és kerekítve egészre megkapod a v2 értékeit, majd ezeket összeadva a kapott értékeket 100-ra átsúlyozva kapNÁD v1-et, de ez nem igaz, ezen még agyalok kicsit, lehet az okozza az eltérést, hogy az egészre kerekített v2-ket adjátok ti össze, nem a pontosabb értékeket...
Szóval amit leírtam az ezt tudja:
-
 #4003
#4003
újabb feladattal fordulok hozzátok, faternak kellene:
adatok:
vonalintegrálás témakörén belül kell megoldani ezt a feladatot
és ez egy cikloisz ív
-
napstR #4002 Sziasztok!
Remélem valaki tud segíteni, mert iszonyatosan fontos lenne. Két komplex rendszert kell összehasonlítanom a KIPA-módszerrel. Ehhez a Guilford-féle eljárással kell megállapítanom 17 értékelési tényező súlyszámát.
A kapott skálaértékeket úgy kéne transzformálnom, hogy a súlyszámok összege a 0-1 vagy a 0-100 intervallumba essen. Ez a KIPA-módszer egyik feltétele.
Mutatom mire gondolok:
Ebben a preferenciamátrixban az P a preferenciaarány, u a prenferenciaarányhoz tartozó standard normális eloszlás értéke. A Z értékek az u-(umin)/umax-umin képlet alapján lettek kiszámolva.
Ezek után a v1 és v2 súlyszámokat úgy kapták meg, hogy a Z skálaértékeket transzformálták. A KIPA módszerhez 100 összegű súlyszámok kellenek míg a Kesselring-féle összehasonlítási eljáráshoz 2-10 közé kell a súlyszámokat megválasztani. Viszont nem sikerül rájönnöm milyen képletek alapján tették ezt.
Az intervallumskálát elvileg az f(x)=mx+c függvénnyel lehet transzformálni, ahol m # 0. Sajnos én ettől sem lettem okosabb. Talán Ti tudtok segíteni! Akármelyik, esetleg mindkettő transzformációhoz használt képlet jól jönne! :(
Előre is nagyon köszönöm! -
 #4001
#4001
Találtam egy zseniális meglátást is:
What the above solutions forget is exploiting the fact that when the stones allow you to weight an object with weight X and they allow you to weight an object with weight X+2, you can implicitly weigh something with weight X+1 by stating that it is heavier then X but lighter then X+2 ( And it must be integer ).
Ez egy nagyon jó ötlet, ez például eszembe sem jutott volna. (A lényege, hogy ha valami tömege X+1 és ezt leméred egy X-el, majd X+2-vel és először azt kapod, hogy X-nél nehezebb, de X+2-nél könnyebb, akkor a tömege X+1, mert a tömegek egészek. - Zseniális!!!)
Bizonyításon nem gondolkodtam, brute-force algoritmust választottam volna én is, mivel elég kis adatkupacon kell végiglépkedni. -
commissioner #4000 Ehhez én kevés vagyok... :D úgyhogy utánanéztem a neten: ezen a helyen ránézésre elég jó bizonyítások vannak egyes kommentekben. Alapvetően brute-force eljárást keresett a blogger, de bónuszként a formális megoldásra is kapott válaszokat.
A legérdekesebb, h valaki úgy kezdte el fejben megoldani a feladatot, h vette először az 1-et. Majd ennek vette a kétszeresét és hozzáadott egyet, így lett a 3. Mivel megkapta így az 1-et és 3-at, ezeket összeadta, majd szintén vette a kétszeresét plusz egyet, így megkapta a 9-et. Ezután az (1+3+9)-et kétszerezte meg és adott hozzá egyet, amiből meglett az utolsó szám is, a 27.
Egyszerű algoritmus, de miből gondolta, h ha így számol, akkor rögtön megkapja a keresett számokat? -
 #3999
#3999
Háát, én tényleg tippeltem, h jó lesz, de ebben az játszott némi szerepet, hogy:
- Régebben "sokat" foglalkoztam azzal, miért nem 1 és 3 értékű érméket használunk (ez ugye csak 2 féle), miért 1, 2 és 5 értékűeket (ez 3 féle). Ezeknek a decimális többszöröseit legyártani többletköltség (1.5x annyiba kerül?!?)
- Szintén régebben érdekeltek a negatív alapú számrendszerek és azoknak a matematikája. Ilyen számrendszerben csak összeadást kellene használni - ez volt az alapgondolat, mindig problémásnak éreztem a kivonó rutinokat.
A fenti két "előélet" pont illett ehhez a feladathoz. Lehet légből kapott a gondolat, hiszen nem kell a számrendszer helyiértékeinek lennie a négy számnak. Hiszen lehetne pl. 1+2+10+27 is, de nem biztos hogy ez jó.
Az én gondolatmenetem matematikára fordítva olyasmi, hogy milyen alapú az a számrendszer, amelyben a legkevesebb jeggyel előállíthatóak a pozitív egész számok 1-től 40-ig és ... itt kellene ügyesen a "kétkarú mérleg"-ből eredő "kivonást" megfogalmazni okosan.
Tudom, nem sokat segítettem ezzel... -
commissioner #3998 A bizonyítás megvan ahhoz, h miért pont 1,3,9,27 a megoldás? (ill., h ez-e az egyetlen megoldás) -
 #3997
#3997
1 = 1
2 = 3-1
3 = 3
4 = 1+3
5 = 9-(1+3)
6 = 9-3
7 = 1+9-3
8 = 9-1
9 = 9
10 = 1+9
11 = 3+9-1
12 = 3+9
13 = 1+3+9
14 = 27-(1+3+9)
és innen lehet folytatni a fentiek kivonogatásával 27-ből, majd 27-től a hozzáadogatásával. -
polarka #3996 40 fontos 4 darabra tört -
 #3995
#3995
Nem ismerem, de ha 4 részre lenne betippelném a 1+3+9+27 -et.
Mivel "kétkarú" kivonni is lehet, azaz a mérendő test mellé is lehet súlyt pakolni. Alaposabban kéne nekiesnem - de még nem is kávéztam... -
 #3994
#3994
helló!
keresek egy régi matek feladványt, de már nem emléxem pontosan a feladat szövegére, vmi ilyesmi volt:
egy görög kereskedő leejt egy 40 fontos követ, ami 3 darabra tör, utána észre veszi, hogy ezzel a három darabbal 40 fontig bármit (egész számú tömeg) le tud mérni egy két karú mérleg segítségével.
a konkrét számokban nem vagyok biztos -
 #3993
#3993
A forgó egységvektor itt az 'e'
Itt pedig 8.oldalon van leírva.
Hétköznapi életben pl ciklois/epiciklois pályagörbéjének tetszőleges pontja adható meg vele.
SPOILER! Kattints ide a szöveg elolvasásához!Egyáltalán nem tudod használni a google-t! -
gregtom6 #3992 Milyen az a forgó egységvektor? Vagy forgó vektor.
Google-t tudom használni, és nem segített. Kösz a helpet. -
polarka #3991 Sztem próba, szerencse alapon ment ennek a megoldása.
ám találtam néhány érdekes dolgot:
Virtual Math Museum
Paul Nylander's HP -
 #3990
#3990
Most is mint mindig, tudatosul bennem, h túlképeztek az ilyenekhez 


Annyira, de annyira egyszerű és nem tudok rájönni...


-
polarka #3989 lehet félreérthető voltam... -
 #3988
#3988
oksa, akkor nekiülök,de 9-10 előtt nemigen leszek gépközelben!
hali! (és kösz a gyors választ!) -
 #3987
#3987
igen, kiemeléssel kellene állítólag megoldani. énis próbálkozom vele -
 #3986
#3986
csak 1 kérdés, biztosan ez az egyenlet?
vége a melónak és küzdök vele kicsit, ha ez a feladat valóban?!
-
polarka #3985 Sztem ez a feladat nem primitív.
(x^2-x-5)-öt kéne kiemelni és akkor már meg lehet oldani.
De erre a sejtés miatti próbálgatáson kívül más indokot nem tudok. -
 #3984
#3984
sziasztok ne haragudjatok hogy egy ilyen primitív feladattal állok elétek, de a kistesómnak lenne és gimis módszerekkel kellene megoldani ezt (új ismeretlen bevezetésével), az x köböt nemtudom hogy hogy lehet kiküszöbölni
-
polarka #3983 physorg
space.com
Éppen folyadékkristály (LC) polarizációs hatásait méregettük. Nah mármost, azokban is szerves, királis molekulák vannak. Tehát tulajdonságaikat tekintve pont erről van ez esetben is szó. Ezen molekulák anizotrop viselkedése abban nyilvánul meg, hogy egyik irányban a fény más törésmutatóval képes végighaladni. Lássuk ezt egy példán:
Adott egy párhuzamos LC cella (hasáb)
párhuzamos:= a molekulák mind ugyanabba az irányba állnak (nem a fény haladási irányával megegyezően)
Ekkor érkezzen be egy olyan síkban poláros fény, amely a cella egyik kitüntetett irányával (optikai tengely) Θ fokot zár be.
Ekkor a fény térerőssége felbontható két olyan egymásra merőleges összetevőre, ahol az egyik az optikai tengely irányába mutat, a másik pedig arra merőlegesen. Világos, hogy mivel különböző sebességgel terjednek, így mire a túloldalon kiérnek az egyik fázisa egy állandóval el lesz tolva az előzőhöz képest. Ha ezeknek újra a szuperpozícióját képezzük, akkor Lissajous-görbék mentén változó polarizáltsági kapunk (elliptikusan poláros).
Itten ezek a szakik meg azt állítják, hogy az élőlények egységes kiralizáltsága a visszavert fényben okoz akkora mértékű ilyen, egyirányú cirkularitást, hogy az kimérhető, talán még távolról is. Hogy mit hoztak össze ebből azt nem tom, de nem elképzelhetetlen. -
 #3982
#3982
Mindjárt gondoltam, POLÁRka 



Amúgy tényleg igaz az, h egy bolygón ha van élet, akkor a rajta levő növényzet a ráeső napfényt csak egy síkban polarizálva veri vissza, míg a szervetlen és élettelen felszínnel rendelkező bolygók pedig nem?
Azért nem értem ezt a dolgot, mert már egy vízfelület, sőt bármilyen tükröződés is "kiválasztja" egy bizonyos síkban rezgő fényt, ezért hogyan lehet a két esetet elkülöníteni? -
polarka #3981 Ha vkit esetleg érdekel, a fény elliptikus polarizációjával kapcsolatban merült fel a probléma. -
polarka #3980 No, megvan. Csak egyszer elírtam a levezetést, aztán meg észrevettem, h benéztem egy annyira szemet nem szúró dolgot. -
polarka #3979 Adottak az alábbi parametrikus görbék (Lissajous):
x=sinΘsin(t+δ)
y=cosΘsint
ahol t=0..2π; δ=áll.; ΘϵR
Ezek általában 2 helyen is metszik az y=-tg(Θ)x egyenest.
Kérdés, hogy mely Θ értékeknél lesz ezen két metszéspont a legtávolabb egymástól?
Biztos vagyok benne, h Θ=π/4+kπ/2; kϵZ lesz a mo., de ezt analitikusan hogyan hozható ki? -
polarka #3978 huwiki se maradjon le -
polarka #3977 igen
Methods of matrix inversion enwiki
inverse matrix part 1 khanacademy
inverting matrices part 2 khanacademy
inverting matrices part 3 khanacademy
PatrickJMT:
Finding the Inverse of a 3 x 3 Matrix using Determinants and Cofactors – Example 1
Finding the Inverse of a 3 x 3 Matrix using Determinants and Cofactors – Example 2
Finding the Inverse of a 3 x 3 Matrix using Determinants and Cofactors – Example 3 -
 #3976
#3976
hali!
kérdés:
ha egy mátrix inverzét akarom kiszámolni, akkor minden esetben kell-e az aldeterminánsok mátrixát transzponálni?
mert volt két példafeladatom az órai jegyzetemhez, egyiknél az 1/det(aldeterminánsok mátrixa)T volt a feladat megoldása, a másiknál meg csak szimplán az 1/det(aldeterminánsok mátrixa), most utóbbinál a tanár hagyta le véletlenül vagy valamikor nem kell sor/oszlopcsere a végén?