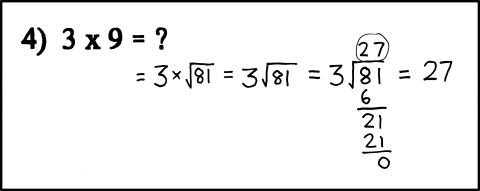739
A FERMAT SEJTÉS története
-
forrai #138 Valaki korábban a szememre hányta, hogy én csak szövegelemzéssel foglalkozom?
Engem pedig mélyen felháborít az a tiszteletlenség, és felületesség, ahogyan a matematika Fermat szellemi örökségével- annak a két mondatnak az átértelmezésével foglalkozott.
Nem tudom, hogy a MATEMATIKA (a nagybetűs) hogyan fog ettől elhatárolódni, és megtisztulni.
Kívánok hozzá jó egészséget mindnyájunknak!
-
forrai #137 A hatványösszeg elmélet mreglepően összefogottá teheti bizonyos számelméleti feladatok megoldását, azonban az egyetemi képzésenn se találkoztam még a nevével se.
A matematika éppen úgy túllépett rajta, mint az árapályon a fizika.
Nekem meg ezek még felfoghatók, kezelhetők.
Örülök a feledékenységüknek. -
forrai #136 Miért, ezt a fórumot nem Sophie Germainről nevezték el (SG...)? Én eddig azt hittem...(ezt az észrevételed méltányolom)
Megérdemelné, mert pont azért, mert nő volt, a matematikusok nem fogadták be igazán őt! Még az egyetemet is álruhában végezte el (valaki helyett).
A matematikusok rátartiak, nem fogadnak maguk közé akárkit: nőket, bírókat, gépészmérnököket...Kivételesen talán milliomosokat, vagy a menzai főszakácsot, de azokat is, csak ha megérdemlik. :-) -
forrai #135 Mindez 25 évig eltartott. Hogy elfogadják, ahhoz nem elég az univerzum.
Ezért összefoglalom még egyszer!
1. Fermat, a kor eszközeivel (főképp saját felfedezéseivel, pld. kis Fermat képlet)azt bizonyította, hogy az ....képletnek van megoldása, csakhogy az végtelen számosságú számjegyből áll, s így NEM FELÍRHATÓ, NEM FÉR EL A MARGÓN!
2. Fermat és az idő tréfája következtében ezt az értelmezést feledve később olyan bizonyítások születtek (előbb parciális, majd generális), amelyek nem Fermat sejtését és tételét, hanem a saját értelmezésüket vizsgálták és bizonyították, hogy MEGOLDÁS NEM LÉTEZIK!
Sajnálom, de én így látom a helyzetet, és elegett vizsgálódtam, hogy ne hagyjam magam "elhesegetni".
Várom a véleményeket. -
forrai #134 Először átalakítottam a Fermat képletet polinommá, a hatványösszeg elmélet segítségével.
Majd azt a polinomot általánosítottam bármely hatványra, amit már vizsgálni lehetett.
Szinte kezdettől ezt a bizonyítási utat próbálgattam. Az említett d-osztó bizonyítás is hamar megvolt, és kedvet adott, hogy bizonyítsam: minden d=2kn+1 prím oszt kell, hogy legyen!
Először csak polinom osztással győzödtem meg arról , hogy az első d-k csakis a változók osztói lehetnek. n=3 esetén nemcsak d=7, hanem a 13, 19, stb. Némelyik polinom osztás már szinte kínos volt.
Az általános bizonyítást kellett megtalálni.
Az viszont cseles, és váratott magára. Nem mondhatnám, hogy elfér egy szokásos margón. Azonban egy jó szélesen, igen apró betűkkel, nemcsak az enyém, de Wilesé is elférne.
Fermat biztos nem olyanra gondol, ami valahogyan elférne...
Amikor tréfált- azt is komolyan vette. -
forrai #133 Pio
Így van. Végtelen számosságú ilyen d prim létezik bármely n páratlan hatványhoz.
Egyik nagyobb a másiknál. És a Fermat sejtés esetén (ahogyan bizonyítom), nemcsak a k=1, hanem az összes többi így képezhető, végtelen számú, és nagyságú d osztónak (továbbá más osztóknak is, pld 2.) osztania kell valamelyik a;b;c változót.
Ettől vállnak olyanokká, hogy nem felírhatók.
Vagyis pont úgy "irracionálisak, ahogyan a köbgyök 35, ami szintén nem felírható. Csakhogy ez egy egész szám, és nem törtszám.
Fermat ezzel mintegy szimmetrikussá tette az irracionális számsikot.- a törtekhez egészet is adott. Csakhogy ezeknek az egészeknek csupán a bináris számrendszerben ismerhető meg az első jegye: az egység.
A többi határozatlan.
Kezdetnek ennyit róla.
Számomra ennek tükrében tisztán olvasható a latin szöveg értelme:
"Nem felirható, mert nem fér el a margon." Nem pedig, hogy nem megoldható! Amit mindenki vizsgált.
Én is csak azért érthettem meg, mert így forog az agyam. Vagy áll. Ki hogy gondolja. -
forrai #132 Bnum, ne keverjük a dolgokat.
Sophie Germain csupán az első lépést tette meg, adott n-nél, k=1-re.
Én meg azt bizonyítottam, hogy adott n-nél bármely k-ra, amelynél csaklétezik a prim. Valamint azt is (kiegészítőleg) hogy bármely n-re végtelen számú ilyen d prim kell, hogy létezzen, természetesen nem minden, csak bizonyos k-hoz.
Ez egyáltalán nem egy fortély nélküli bizonyítás. Ide se szívesen hoznám. És ez csak a könnyebb része. -
forrai #131 Pio
Próbálj kicsit figyelni.
Egy adott n-hez bizonyítom, hogy kell végtelen sok d prime legyen... Az kicsit más...
Örülök, ha nem kéritek, és így is elfogadjátok.
A másik, hogy Sophie Germain csak a k=1 esetre bizonyitotta.
Vagyis n=3,akkor d=7
n=5, d=11
stb.
Én viszont azt bizonyítottam, hogy n= 3 esetén d=7;13;19;... mind a változó osztója.
Ez pedig nem könnyü.
Ehhez létrehoztam a hatványösszegek elméletét egy új felfogásban (az létezik már a XII. századtól, sőt, talán régebben, pld. a Newton-Girárd képletek)
A hatványösszegek elmélete tette lehetővé csak, hogy a d osztókat végtelenig bizonyítsam.
Továbbá, hogy bizonyítsam: az elliptikus egyenlet a+b+c=0 esetén nem folytonos.
Mellékesen létrehoztam egy iteráció nélküli eljárást a magasabb hatványú egyenletek valós gyökeinek meghatározására.
Nem illik lehülyézni még magamnak se magam, de megteszem, ha az nektek szimpatikus. -
Pio #130 "Nem kellett hozzá túl ravasz ötlet. Csak azt kellett bizonyitani, aminek első lépését később Sophie Germain is megtalálta, felvillanyozva vele Gausst is.
Hogy nemcsak a k=1 eset, hanem a d=2kn+1 primek mindegyike is a változók osztója kell, hogy legyen."
Ebből arra gondoltam, hogy forrai nem is csak az prime(n), k:=1 esetről beszél, amik a SG (esgé :D ) prímek, hanem ennél is többről, szerinte n tetszőleges párossal szorozható.
Aztán jött ez: "Miért ne bizonyítsam, hogy a d=2kn+1 alakú prímosztók száma végtelen?"
Ami fura volt, mert tényleg mintha azt sejtetné, hogy egy (persze az SG prímekénél bővebb) halmazról be tudja látni, hogy végtelen (gondolom megszámlálható). Persze lehet, hogy erről a halmazról már rég tudjuk, hogy megszámlálható, nem vagyok túlságosan képben, csak annyit tudok, amit belémsulykoltak az egyetemen. :(
Akkor félreértettem. Megjegyzem nem nehéz félreérteni azt, amit forrai ír... :( -
Bnum #129 Elvileg lefedheti, de k nem lehet tetszőleges.
Tehát a halmaz azért ettől kevesebb.
A Sophie Germain prímek viszont nem lehetnek ilyen alakúak. -
Pio #128 Tetszőleges k-ra és n-re nyilván végtelen sok van, hisz tetszőleges k-val és n-nel 2kn+1 az összes létező páratlan számot lefedi, így minden prímszám belekerülhet, azokból pedig végtelen van, amit ha jól emlékszem már valamelyik híres görög is bebizonyított viszonylag egyszerűen.
Szerintem forrai Mester a Sophie Germain prímekről beszél, amik azok az n prímek, melyekre 2n+1 is prím.
Például n=11 prím, 2×11+1=23 is prím, akkor 11 egy Sophie Germain prím.
Azt, hogy ilyenből végtelen van-e eddig senki nem tudta bizonyítani, talán majd most forrai, addig vissza is favolom a topikot... :) -
Bnum #127 A 2kn+1 alakú prímek száma lehet végtelen, ha megfelelő a k és az n.
Az osztók száma viszont véges. -
forrai #126 Privát válasz ment. Látom, hogy Önnel tárgyszerűen lehet levelezni.Akkor nem veszem fel a szokásos sündisznó- állásomat. -
gregtom6 #125 Mint írtam, nem rosszindulatból mondtam, csupán nem a megszokott hétköznapi stílussal írja azt, amit ír.
Tehát jelenleg nem tudnám eldönteni, hogy Önnek írónak kellene lenni, vagy matematikusnak. Vagy éppenséggel mindkettőnek:)
És gondolom a sejtésem nem csal, hogy Ön matematikus. -
forrai #124 Hát lássak neki bizonyításnak?
Egy két egyszerűbb dolog ide is elférne. Miért ne bizonyítsam, hogy a d=2kn+1 alakú prímosztók száma végtelen? Persze mindegy, hiszen ha nem bizonyítom, hiányolják, ha meg bizonyítom, azt mondják, hogy triviális. Jól sehogy se jöhetek ki, ilyen az élet.
De legalább telik az idő.
Szóval azt kellene bizonyítsam, hogy bármely d=2nk+1 alakú prímek végtelen számosságuak, és egyik nagyobb, mint a másik (hátha ezt is kell?)
Nincs kedvem nekikezdeni, mert munka ez is, és minek?
Valakit azért érdekel? Mert ez is része Fermat valószínű bizonyításának!
-
 #123
#123
8 év általános nem volt elég?:) -
forrai #122 "Magam
Vagyok
Nagyon,
Kicsordul
A könnyem
Hagyom" -
forrai #121 Nézd, jól esne, ha valaki tanítana fogalmazni- azt mindig is megköszöntem. Érdekelne az is, mit találtál furcsának benne, mert tanulni akarok. Írd ide, vagy privát. Kösz, viszlát. Ja és bárki más is. -
forrai #120 Pio, már-már hinni kezdtem benned! És sajnos, nem is csalódtam. De mit vártál itt? Hogy himnuszt éneklek a Fermat sejtés kiforgatásáról?
Hát nem látod, hogy azt történt?
-
Pio #119 Jó, feladtam, Neked van igazad, az egész egy hatalmas, világméretű tévedés/hazugság, az egész világ félreértette Fermatot, mázli, hogy te lefordíttattad és abból mindez egycsapásra kiderült.
Valószínűleg a wombatok, a Sátán bérgyilkosai állnak a háttérben.
További jó szórakozást!
-fav -
forrai #118 "Nemigen etikus
A nemi genetikus!" -
forrai #117 Dehogy is. Én Wilest igen nagyra becsülöm, ahogy mindenki más is. De főképp azért, mert a szétzilált matematikába vitt egy kis reménysugarat, hogy távoli ágai összeköthetők.
A Fermat sejtéshez viszont nincs köze, mert az egész másról szól- a megoldás felírhatóságáról.
Ha te 2 tányér húslevest rendelsz, nem örülsz, ha paprikáskrumplit hoznak.
Itt pedig bizonyítottan ez történt. -
forrai #116 Magánzó vagyok. Más néven csődör. Vagyis biztos csőd. Talán csődbiztos.
Nagyon unalmas. Ülsz vársz egy csődre. Csőd jön, bemutatkozunk, stb. Közbe sok időm marad. Ja és világító toronyőr is vagyok. De sajnos torony nincs, s így én világítok. Könnyű, mert úgyis mindig csak égek...
-
Bnum #115 Te meg a genetikusok képességeit becsülöd le. -
 #114
#114
-
Bnum #113 Azt írsz amit akarsz, az igaz lesz, vagy tévedés, de ne akard Wilest tettét kisebbíteni.
Vele kapcsolatban az elismerésen kívül csak annyit lehet megemlíteni, hogy 20. századi eszközökkel oldotta meg a bizonyítást.
Te ehhez hozzá tehetsz (ha tudsz), de elvenni ne akarj! -
gregtom6 #112 Valamint azt se tudom eldönteni, hogy neked inkább a reál, vagy mégis talán a humán tárgyak állnának közelebb, mert nagyon furán fogalmazol, persze ezt ne vedd sértésnek. -
gregtom6 #111 forrai-nak ment az előző kommentem. -
gregtom6 #110 Heló!
Te valami nagy matematikus professzor vagy? Mivel foglalkozol pontosan? Nagyon kíváncsi lennék, hogy hogy vetted rá magad, hogy ilyen matematikai filozofálgatást kezdeményezz. -
forrai #109 Pio, te vagy csak a vigaszom! Legalább ne mondj hazugnak! Ühüm-bühüm...zokogok.
(nem lehet mindezt nem lazán venni, ha komolyan venném, belepusztulnék)
Elküldtem külön fordítatni. Szótáraztam is. Nem megyek fogorvosnak, pusztán, hogy latinul tanuljak! Képzelj el egy fogtömést, általam! Nem, tisztán humánus érzésből lemondtam erről. Most meg a szememre veted?
-
forrai #108 Félreértések vígjátéka, mint egy Papp Jancsi vicc: ez a tudomány:
1. Egy csodálatos elme leír egy érdekes sejtést, és a megoldását, a kor szokásainak megfelelően, játékosan, (vagy komolyan) kódolva.
2. A könyvi kiadás során az utolsó mondata végén, amit ő feltehetően üresen hagyott, hogy-hogy nem megjelent egy bizonytalan, oda nem illő írásjel, tönkretéve a megfejtés kulcsát.
3. Az eredeti kézirat eltűnik.
4. Az eredeti kézirat legkülönbözőbb változatai keringenek, mindenki azt oldja meg, amit úgy gondol, hogy tud.
5. Az eredeti bizonyítási formula, hogy NEM LEHET FELÍRNI, megváltozik: NEM LEHET MEGOLDANI.
6. Nyakatekert bizonyítási séma születik a megváltozott formulára, amelynek egy része kiváló, és dicső, arról sokat beszélünk, más része viszont megalapozatlan.
7. Végül merik azt állítani, hogy Fermat a saját tételét nem oldotta meg? Egyébként igazuk is van! Mert Fermat valóban egészen mást oldott meg, míg ők semmit (a segédtétel kivételével)!
Mondom, mint egy Papp Jancsi vicc, olyan. De nem, ezt már nem veszi be a hasikám!
-
Pio #107 Te egy magyar fordításból vonsz le következtetést, ám Fermat francia volt és (úgy tudom) latinul írta fel ezt a dolgot. -
forrai #106 "Lehetetlen egy köbszámot FELÍRNI két köbszám összegeként..."
Vagyis nem azt írja Fermat, hogy nincs megoldás, hanem azt, hogy azt lehetetlen felírni.
Ezek után nem minősítem azt, aki az ellenkezőjét állítja, vagyis azt, hogy nincs megoldás.
Annyit, hogy bizonyára nem hazudik, de nem a Fermat sejtésről beszél.
Kedves Bnum, és többiek: ha többi nem volt elég, ez talán már elégséges érv? Gondolkodjatok el rajta! -
forrai #105 Nem kellett hozzá túl ravasz ötlet. Csak azt kellett bizonyitani, aminek első lépését később Sophie Germain is megtalálta, felvillanyozva vele Gausst is.
Hogy nemcsak a k=1 eset, hanem a d=2kn+1 primek mindegyike is a változók osztója kell, hogy legyen.
Sajnos, vizsgálataim alapján én már nem tudok elfogadni egy olyan bizonyítást, ami azt állítja, hogy NINCS MEGOLDÁS!
Csak olyant tudok elfogadni, hogy VAN MEGOLDÁS, de NEM ÍRHATÓ FEL!
(vagyis hogy irracionális, megismerhetetlen). Mert ez volt FERMAT MEGOLDÁSA IS! Nézd csak meg...(...nem lehet felírni...)
Ezért akárhányan és akárhányszor nézték át Wiles bizonyítását a Taniyama-Shimura sejtésről, a Fermét sejtés bizonyítását tőlük mégse fogadhatom el. Dolgozzanak 22. ik századi módszerekkel, hátha jobban összejön majd.
Azért ne írd te se itt, hogy bárki hazudik. Mert aki ezzel a problémával foglalkozott, akkor se szolgál reá, ha netán tévedett. -
forrai #104 Szóval mondom, bizonyítottam. Bizonyára lehet bizonyítani 16. századbeli módszerekkel is, de arra nem vágyom már. Aki akar, gondolkodjon. -
forrai #103 "Hát amit állítasz ez nem tévedés, közelebb van a hazugsághoz."
De hiszen az alaptételben van a hiba, amit nem Wiles csinált. Ám én nem mondanám róluk, hogy hazudtak. Azért az nagyon súlyos vád. Dehonesztáló. Kérlek, ilyet ne állíts. Én is inkább tévedésnek veszem.
"Tehát azon lehet gondolkodni, hogy lehetne bebizonyítani, 17. századi módszerekkel."
Elmondtam már, hogyan bizonyítottam XVII. századbeli módszerekkel.
Pontosabban Te a bizonyításom is ismerheted. Abban azt bizonyítottam, hogy minden d=2kn+1 prim az a;b;c változók osztója kell, hogy legyen.
Azzal van problémád? Kiváncsi vagyok.
-
Bnum #102 Hát amit állítasz ez nem tévedés, közelebb van a hazugsághoz.
Ha olvastad SIMON SINGH: A nagy FERMAT sejtés c. könyvét, akkor tudhatod, hogy igencsak szétszedték a bizonyítását. Hibát is találtak benne, ami menetközben lett kijavítva.
"Wiles matematikával sűrűn teleírt 100 oldala kétségkívül eleget tesz ennek a feltételnek. De a francia ma¬tematikus bizonyára nem alkotta meg évszázadokkal mások előtt a moduláris formákat, a Taniyama-Shimura-sejtést, a Gabis-csoportokat és a Kolyvagin-Flach-módszert.
Ha Fermat nem úgy bizonyította állítását, ahogyan Wiles, akkor mégis hogyan? Erről a kérdésről a matematikustársa¬dalom kétféleképpen vélekedik. A keményfejű szkeptikusok meg vannak róla győződve, hogy ez az utolsó tétel a tizenhetedik századi géniusz egy ritka gyenge pillanatának szüleménye. Szerintük voltaképpen hibás bizonyításról írta Fermat a lap szélére, hogy "Igazán csodálatos bizonyítást találtam erre a tételre..." Hogy milyen természetű lehetett ez a hibás bizonyítás, az vitatható, de nagyon is lehetséges, hogy ugyanazt az utat követte, mint Cauchy vagy Lamé munkája.
Más matematikusok, a romantikus optimisták, továbbra is hisznek abban, hogy Fermat-nak volt egy zseniális bizonyítása. Bármi volt is azonban ez a bizonyítás, tizenhetedik századi módszereket használt, és olyan ravasz ötletre támaszkodott, amely Eulertől Wilesig mindenkinek elkerülte a figyelmét. A Wiles-bizonyítás publikálása után is számos matematikus bízik még abban, hogy hírnevet és dicsőséget szerezhet Fermat eredeti bizonyításának felfedezésével."
Tehát azon lehet gondolkodni, hogy lehetne bebizonyítani, 17. századi módszerekkel. -
forrai #101 Kedves Landor.
Hozzásegítettél a kávémhoz, mert összejött a 100-ik hozzászólás, nagy nehezen.
Igazából csak félreértettelek, mert te a 3,141na-ra gondoltál, én meg erre itt- ni: oIo

No, hát írjál: te vagy az első (második) aki képletet is ír. -
forrai #100 "örülni kell, hogy bebizonyította Wiles"
Hát Wiles nem azt bizonyitotta be! És innen kezdődik a csúsztatás, ami fedi a valódi történetet!
Ezt bárki, aki ehhez picit is ért, tudhatja!
Mondom: ő egy segédtételt bizonyított csak, ami a matematika számára más szempontból- az egységesítése miatt fontos!
Így furcsálnod inkább azt kellene, hogy miért nem a bizonyítás útját lefektető Freyé a dicsőség? Róla azonban senki se beszél. Ha valóban jó a bizonyítása, én ezt méltánytalannak tartanám. Mert akkor ő a Fermat- sejtés igazi bizonyítója! (most a kötőjel is idejébe jött, és ráadásul szinte önkivületben- ez igazán nagyszerű!) -
Landor #99