625
A Maple egy fejlett matematikai problémamegoldó és programozói szoftver.
-
Petko #305 Köszönöm a segítséget!
eleinte nem ment amit írtál, nem akart az a-ra megoldást dobni, és rájöttem hogy az volt végig a gondja, hogy a szorzásnak szükséges kiírni a jelét
majd még próbálgatom használni, hátha beválik mégis -
xDJCx #304
Tovább általánosítva a feladatot, legyenek paraméterek az integrálás határai is (x1, x2 és b paraméterek), hogy függ az a változó ezektol?:
![]()
-
xDJCx #303 Egy fokkal általánosabban a feladat, itt b egy paraméter.
Enterezve a beviteli sorokat, az utolsó beviteli sor eredményéének végére állva jobb kattintasra elojön a solve equation for a variable menu, itt a-t választani, így megoldja a-ra az egyenletet, b paraméter függvényében.
![]()
-
xDJCx #302
Ha függvényként akarjuk megadni az integrálandó kifejezést akkor így lehet:
![]()
Nem kell kijelölni több sort, hanem az utolsó sorban, a kifejezés után állva kell a jobb kattintás és solve ekkor.
Persze most a feladat elég triviális.
-
xDJCx #301 Legegyszerubben így lehet: a beírt sor után jobb egér kattintás és solve:
[IMG]![]()
[/IMG]
-
xDJCx #300 Ez nem a program bénasága... Érdemes a helpbol pl. a new user's touron véggimenni, nekem 10-es van, de biztos ugyanígy van a 11-esben is. Meg van magyarul könyv is. Általában az eredményen kell jobb gombbal kattintani. -
#299
Nekem még soha nem jutott eszembe az, hogy jobbkatt solve... :S -
Petko #298 de itt a minta hogy miről beszélek:
![]()
most valaki árulja el hogy mi az isten szerelméért képtelen egy kurva matek program is nekem annyit megtenni hogy beirom az első két sort, kijelölöm és jobbklikkben solve for a numeric value vagy ilyesmi.
teljesen kézenfekvő számomra hogy egy ilyen programot ilyenre, és így akarok használni -
Petko #297 nézegettem matek programokat, évente egyszer ráveszem magam hogy valami matek programmal elkezdek dolgozni de mindíg agyilag felbasznak
most pl leszedtem a maple 11 et
de basszus lehet velem van a baj, de egy ilyen qrva matek programtol annyit várnék el hogy ha már ott a nagy duma, hogy beírok egymás alá 3 definiálsát és akkor egy változóra kidobjon valamit de az istenért se tudom megcsinálni azzal a kurvára felhasználóbarát felületével
most én vagyok gyökér vagy tényleg minden matekprogram ilyen kurva béna? -
#296
hmm.. ha ilyen jó reklámja van, akkor majd megpróbálok beszerezni egyet :) -
xDJCx #295
Szívesen.
De remélem nézegeted párhuzamosan a jegyzetet is. Ez egy összetett feladat, és csak az elso lépése, hogy mátrixos alakban fel tudja írni az ember, elokerül több fogalom a lináris algebrából még ezen kívül mátrixhatványozás elvégzésénél: diagonális mártix, diagonizálás, sajátértékek, sajátvektorok... Ezeket jó megérteni hozzá, különben nincs értelme.
A maple 10-es megoldásnál ezeket nem kellett kézzel végigcsináltatni, mert kapásból tudta a szimbólikus n-edik mátrixhatványt számolni, és ennek a hatérértékét venni (n-> végtelen). Lehetne a kézi módszer lépéseit is végigcsináltatni vele, ez tanulságosabb is lenne, de a régi mapleben lévo linalg csomagot már régen hazsnáltam.
Mindenesetre jobban járnál a 10-es maplellel, többet is tud és könnyebben kezelheto.
-
#294
Még nem is mondtam, hogy köszönöm!
De köszönöm! :)
Most nézegetem... -
xDJCx #293 Maple 10-hez van ezen az oldalon bevezető kezelési leírás angolul, meg egyebek hozzá:
http://www.engineering.usu.edu/cee/faculty/gurro/Maple.html -
xDJCx #292
Hosszú távon a lakások számának megoszlása (azaz ha n->végtelen):
e = 2/9*e1+2/9*a1+2/9*k1, azaz e = 2/9 *(e1+a1+k1)
a = 4/9*e1+4/9*a1+4/9*k1 , azaz a = 4/9 *(e1+a1+k1)
k= 1/3*e1+1/3*a1+1/3*k1, azaz k = 1/3*(e1+a1+k1)
, ahol e1, a1, k1 a kezdeti száma az egyes fajta lakásoknak, ez itt nem volt megadva, de látszik, hogy nem számít a végso arányban mert azonos az együtthatója e1,a1,k1-nek egy-egy sorban, így összegezhetok.
Azaz e:a:k arány = 2/9 : 4/9 : 1/3 hosszú távon ilyen a megoszlása az egyes fajta lakásoknak.
Maple 10-ben ez a megoldás menete:
restart;
with(LinearAlgebra):
M:=Matrix(3,3,[[6/10, 2/10, 0],[3/10, 7/10 ,2/10],[1/10, 1/10, 8/10]]);
v1:=Vector([e1,a1 ,k1]);
map(limit,Multiply(MatrixPower(M,n),v1),n=infinity);
Régebbi mapleben másképp kell, arra most nem volt idom. -
xDJCx #291
Felírsz egy lineáris egynletrendszert, 3 egyenlettel, 3 ismeretlennel, (mert ebben a lépésben n+1. év adatait tekintjük ismeretlennek az n. év adatai függvényében (azok a független változók)) A lináris egyenletrendszer felírható mátrixos alakban, M*x=b ,M itt az együtthatómátrix stb.. Ezt azért jó lenne tudni edigi tanulmányokból, pl. jegyzetet elolvasni.
Ez egy öszetett feladat, a mátrix felírása csak az eleje a megoldásnak.
A mátrixot majd diagonizálni kell, mert mátrix hatványt kell számolni, ami diagonális alakban könnyen számolható. Ehhez a mátrix sajátértékeit, sajátvektorait kell számolni stb... Ezeket mind meg lehet a maplevel csinálni, ha lesz este időm leírom, de ha nem érted a matek részét, akkor nem sokra mész vele. -
#290
ezt majd elemzem még..
viszont az mitől függ, hogy hányszor hányas a mátrix?
ha 3 féle lakás van, akkor 3*3-as? -
xDJCx #289
Ez valami Markov-láncos dolog.
Eloszor az egyenleteket érdemes felirni.
Pl. en jelolje az elhanyagolt lakások számát a mostani n-edik évben, en+1 a következoben, hasonlóan: án, án+1 az átlagosak..., kn, kn+1 kitunoek száma.
ekkor pl. az egyes fajta lakások zsáma az n+1-ik évben:
en+1 = 0,6*en + 0,2*án + 0*kn (mert elhanyagolt lakások 60%-a elhanyagolt marad,átlagos lakások 20%-a elhanyagolt lesz)
hasonlóan:
án+1= 0,3*en + 0,7*án + 0,2*kn
kn+1= 0,1 * en + 0,1 *án + 0,8*kn
Ebbol mátrixos forma eloallithato.
vekn+1 = M * vekn alakban
ahol vekn+1 oszlopvektor: <en+1, án+1, kn+1>,
vekn oszlopvektor = <en, án, kn>
M= [[0,6 0,2 0],[0,3 0,7 0,2],[0,1 0,1 0,8]] mátrix, ha jól néztem az értékeket.
Mivel vekn+1= M*vekn, ezért vekn = M^n * vek1 . M^n-t kell kiszamolni, ebbol vekn es vekn+1 szamolhato lenne vek1 fuggvenyeben, csak vek1, a kezdeti aranyuk nincs megadva., M^n szamolni diagonizalva egyszeru .
Mapleben van a linearis algebrara a linalg csomag, (az ujabb verziokban a LinearAlgebra csomag), ezzel lehet szamolni....
-
#288
Ilyen feladatot télleg meg lehet oldani Maple-lel?
Lakások állapota: elhanyagolt, átlagos, kitűnő
éves statisztika azt mutatja, hogy:
- elhanyagolt lakások 60%-a elhanyagolt marad
- elhanyagolt lakások 30%-a átlagos lesz
- elhanyagolt lakások 10%-a kitűnő lesz
- átlagos lakások 20%-a elhanyagolt lesz
- átlagos lakások 70%-a átlagos marad
- átlagos lakások 10%-a kitűnő lesz
- kitűnő lakások 20%-a átlagos lesz
- kitűnő lakások 80%-a kitűnő marad
Kérdés: Hosszú távon milyen lesz a lakások eloszlása?
Azt tudom, hogy valami mátrixot kell felírni, és hogy diagonizálni kell, de azt hogy hogyan, azt nem tudom. :( -
#287
hát a legfrissebb a maple11, de backup változatban a 10.06-os a legfrissebb, ami elérhető... -
takacsgabor #286 Hali mindeninek!
Érdeklődnék, hogy melyik a legfrissebb Maple verzió és honnan lehet letölteni...
Köszönöm szépen.
TG -
xDJCx #285 Azért google-on is vannak magyar találatok a addíciós tételek- ről, többféle bizonyítással is, nem bonyolultak, gondolom ezeket te is megtaláltad, igazán nem értem mi kellene még róluk. -
xDJCx #284 Az bizony elég régi verzió, nem ártana frissíteni.
-
#283
Így jó Maple 7-ben:
restart:
f:=sqrt(x):
tartx:=-1..2:
tarty:=-5..5:
plot(f, x=tartx,y=tarty);
-
xDJCx #282 Pedig működnie kéne, legalábbis 10-esben nincs vele gond.
Persze a négyzetgyök függvényre nem kéne negatív x tartományt megadni az x=..-ben, esetleg ezért szól a korábbi verzió, vagy tegyél elé egy restartot. -
#281
Nekem ezt így nem fogadja el:
f:=sqrt(x):
tartx:=-5..5:
tarty:=-5..5:
plot(f, x=tartx, y=tarty);
-
#280
köszi! :)
gogült néztem, de még nem adta meg magát nekem.. :))
majd kersek valami okosabbra :) -
xDJCx #279 Többféle módon lehet:
A plotban direkten megadható y tartománya is:
restart;
f:=x^(-2):
tartx:=1..4:
tarty:=0..0.5:# itt megadható az y tartomány
plot(f, x=tartx,y=tarty);
Vagy egy általánosabb mód: a view opcióval az ábra látható része megadható:
restart;
f:=x^(-2):
tartx:=1..4:
tarty:=0..0.5:
plot(f, x=tartx,view=[tartx,tarty]);
(Az addíciós tételek- gondolom a trigonometrián belüli szögek összege stb tételekre gondolsz, kapásból nem tudom hol van a neten összefoglalva, a próbáld google-t, de az angol wikipedian biztos ott van, meg persze minden matek könyvben. Ha lesz időm ránézek. )
-
#278
y:=(x^(-2)):
tart:=1..4:
plot(y, x=tart);
Azt hogyan lehet megadni, hogy az y tengelyen milyen intervallumban ábrázoljon?
Csak mert ez így nagyon buta megjelenítés. -
xDJCx #277 Ez ábrázolástechnikai probléma, de szerencsére erre van plot parancsnak opciója, a discont. Ahol szakadása van a függvénynek, ne kösse össze a pontokat (discont=true).
plot(floor(x),x=-4..4,y=-4..4,discont=false);
plot(floor(x),x=-4..4,y=-4..4,discont=true);
restart;with(plots):with(plottools):
p1:=plot(sin(x),x=-4..4,color=red,thickness=3):p2:=plot(floor(sin(x)),x=-4..4,color=blue,thickness=3,discont=true):
c1:=disk([Pi/2,floor(sin(Pi/2))],1/12,color=blue):c2:=disk([-3*Pi/2,floor(sin(-3*Pi/2))],1/12,color=blue):
c3:=disk([-Pi,floor(sin(Pi))],1/12,color=blue):c4:=disk([0,floor(sin(0))],1/12,color=blue):
c5:=disk([Pi,floor(sin(Pi))],1/12,color=blue):
p3:=plot(0,x=-4..4,y=-2..2, symbol=circle,symbolsize=20,color=blue,style=point,adaptive=false, sample=[Pi/2]):p4:=plot(-1,x=-4..4,y=-2..2, symbol=circle,symbolsize=20,color=blue,style=point,adaptive=false, sample=[-Pi,0,Pi]):display(p1,p2,p3,p4,c1,c2,c3,c4,c5,scaling=constrained,view=[-4..4,-2..2]);
-
#276
hmmm, ööö igen.. csak órán nem voltak függőleges vonalak :)))
télleg a trunc az csak levágja, persze h nem jó... :S
köszi -
xDJCx #275 A floor értelmezése: az a legnagyobb egész, amely kisebb vagy egyenlo a számmal.
Itt a gyógyítás az ábrázolási problémára:
restart;with(plots):with(plottools):
p1:=plot(sin(x),x=-4..4,color=red,thickness=3):p2:=plot(floor(sin(x)),x=-4..4,color=blue,thickness=3):
c1:=disk([Pi/2,floor(sin(Pi/2))],1/12,color=blue):c2:=disk([-3*Pi/2,floor(sin(-3*Pi/2))],1/12,color=blue):
p3:=plot(0,x=-4..4,y=-2..2, symbol=circle,symbolsize=20,color=blue,style=point,adaptive=false, sample=[Pi/2]):p4:=plot(-1,x=-4..4,y=-2..2, symbol=circle,symbolsize=20,color=blue,style=point,adaptive=false, sample=[-Pi,0,Pi]):display(p1,p2,p3,p4,c1,c2,scaling=constrained,view=[-4..4,-2..2]);
-
xDJCx #274 A különálló pontokat itt sem tudta jól ábrázolni, szintén mintavételezési problémák miatt, tehát, pl. Pi/2-ben és -3Pi/2-ben 1 a floor(sin(x)). -
xDJCx #273
Akkor próbáld ki a floor függvényt:
plot(floor(x),x=-4..4);
plot([sin(x),floor(sin(x))],x=-5..5,y=-2..2,thickness=5);
Ezek értelmezésibeli eltérések, a programnyelvekben többféle egészrészt képezo függvényt használnak, így a mapleben is többféle van. pl. trunc, floor, ceil. Ezek mindegyike valaémilyen értelemben az egészrészét képezni a számnak. A matekórán egyféle értelmezést hazsnálnak, nem emlékeztem erre , azt hiszem a floor ami kell.
Ilyenkor eloszor érdemes magát az egészrész függvényt ábrázolni, öszzehasnolítani ami a jegyzetben van.
-
#272
Igen, két warningot ír...
Ellenben nem jó a fv.
Nem azt szerettem volna ábrázolni, amit learjzoltam, hanem a sinus fv egészrész fv-ét
így:
[sin x]
ugyanis, amit kirajzol az az analízistanárnénim szerint nem úgy van... :S -
xDJCx #271 Ha jól másoltad át akkor nem kell hogy hiba legyen benne. Ha két warning ... kezdetu üzenetet ír ki, akkor ezek nem hibát jelentenek, hanem a rajzoláshoz betöltött két csomag (plots, plottools) miatt figyelmeztet, hogy egyes, eddig szabad neveket, jelöléseket lefoglaltak a csomag parancsai, úgyhogy ezek után ezeket nem ajánlatos pl. változónévnek használni ezeket. -
#270
Nahát! Eltatláltam!!!
De jó! :)))
Köszönöm!
monnyuk nekem így is ír ki hibákat -
xDJCx #269 trunc(x) az egészrész
plot(trunc(x),x=-4..4);# az egészrész ábrázolása
plot(trunc(sin(x)),x=-4..4); # lenne a szinusz egészrész ábra de ez így nem muködik, gondolom mintavételezési problémák miatt nem ábrázolja, Persze egyedi értékeket kiszámolja pl.trunc(sin(-Pi/2)).
Ezért egy alternativ megoldás az abrához:
restart;with(plots):with(plottools):
p1:=plot(sin(x),x=-4..4):
c1:=disk([-Pi/2,trunc(sin(-Pi/2))],1/12,color=blue):c2:=disk([Pi/2,trunc(sin(Pi/2))],1/12,color=blue):
p2:=plot(0,x=-4..4,y=-2..2, symbol=circle,symbolsize=20,color=blue,style=point,adaptive=false, sample=[-Pi/2,Pi/2]):p3:=plot(0,x=-4..4,color=blue,thickness=3):display(p1,p2,p3,c1,c2,scaling=constrained,view=[-4..4,-2..2]);
-
#268
Az egészrész függvényt, hogyan kell ábrázolni?
Illetve az egészrész sin x-re jó az, hogy egy vízszintes vonal az x tengelyen és, ahol 1-et vagy -1 -et vesz fel, ott 11, illetve -1 érték...
nah, valami ilyen :D
![]()
-
xDJCx #267 Már a 10.06 (windowsos) is fent van a már itt említett helyen, ez a 10-es legutolsó verziója. -
xDJCx #266 Na végre, megjelent a 11-es.
http://www.maplesoft.com/products/Maple11/academic/index.aspx
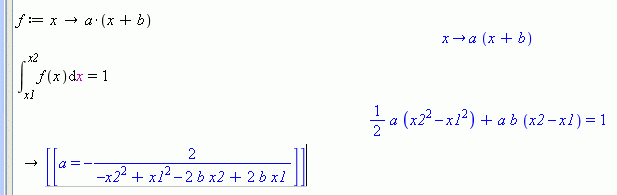
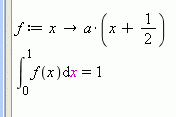
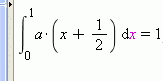[/IMG]
