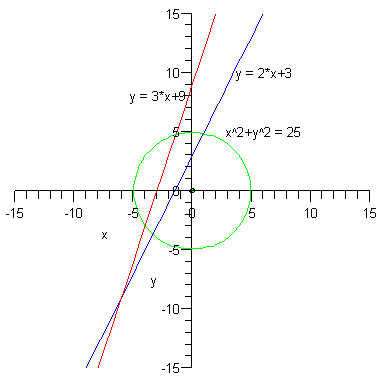625
A Maple egy fejlett matematikai problémamegoldó és programozói szoftver.
-
xDJCx #185 A kettőspont a parancs után azt jelenti, hogy ne írja ki a parancs kimenetét.
A with(plots); # parancsra pedig kiír egy rakás parancsot, amit a betöltött plots csomag tartalmaz. -
xDJCx #184
folyt.:
A feladat szerint milyen alakzatot alkotnak azok a z pontok a síkon, amikre (z-i)i/(z-1) negatív valós szám:
a feltételt szerint f(z) negatív való szám:
azaz Im(f(z)) =0 és Re(f(z))<0 -nak kell ekkor egyszerre teljesülnie.
restart;
with(plots):
kif:=(z-I)*I/(z-1);
z:=a+b*I;
interface(showassumed = 0):
assume(a,real):assume(b,real):
f(z)=evalc(kif); # f(z) = Re(f(z)) + I* Im(f(z)) alakba íratjuk át a fügvényt.
valresz:=Re(kif);
kepzresz:=Im(kif);
# az egyik feltétel szerint f valós része negatív: Re(kif)<0
# ez egy tört: a számlálója és nevezője milyen előjelű lehet?
# a nevező:
nevezo:=denom(valresz);
# ez biztos, hogy nemnegatív, mert ez ilyen alakra hozható:
nevezo=student[completesquare](denom(valresz), a);# két szám nééygzetének összege
# azaz a valós (és a képzetes rész) nevezője is nemnegatív mindenhol, elég a #számlálót vizsgálni:
solve(valresz<0);# hol negatív a valós része f-nek
# egy valós egyenlet, két ismeretlennel: egyik így paraméter, azaz azt mondja #megoldás, hogy függ egymástól a és b.
solve(kepzresz=0);# valós legyen f(z)
# Mivel a és b valós, ezért a kapott megoldásban a gyök alatti kifejezés
# 1-4*b^2+4*b>=0 kell hogy legyen, ez egy másodfokú kif. A gyökei:
solve(1-4*b^2+4*b);
plot(1-4*b^2+4*b,b=-2..2,y=-2..2); # parabola, amely lefele áll, a két gyök között nemnegatív
# az eddigi z=a+b*/I-re kapott feltételeket ábrázoljuk:
# valós részre kapott feltétel:
felt1 := inequal(a < -b+1, a = -2 .. 2, b = -2 .. 2, axes = normal, optionsexcluded = (color = green, thickness = 2)):
# képzetes részre tet feltételből egy kört kapunk, ezt két részre bontva ábrázoljuk:
felt21 := plot([1/2+1/2*sqrt(1-4*b^2+4*b), b, b = -1/2-1/2*sqrt(2) .. 1/2+1/2*sqrt(2)], -2 .. 2, -2 .. 2, axes = normal, numpoints = 1000):
felt22 := plot([1/2-1/2*sqrt(1-4*b^2+4*b), b, b = -1/2-1/2*sqrt(2) .. 1/2+1/2*sqrt(2)], -2 .. 2, -2 .. 2, axes = normal, numpoints = 1000):
sz1:=textplot([-0.7,0.5,"a < -b+1"]):
display(felt21, felt22, felt1,sz1, labels = ["a=Re(z)", "b=Im(z)"],title="z értékek");
-
 #183
#183
a "with(plots):" sor végén miért csak kettőspont van? ahhoz hozzájön a következő sor? -
 #182
#182
köszi!
ezt áttanulmányozom...
és olyat tud a maple, hogy beadok eg fv-t és írja ki a deriváltját.. integráltját? biztos tud, de mi a varázsszó? :)) -
xDJCx #181
Az 2+5*I az egyetlen pont (helyvektor) a komplex számsíkon, nem függvény. Eprzse fel lehet rajzolni ezt apontot, vagy vektort pl. arrow. Lásd korűábban.
De nézzük a kérdéses függvényt:
általában egy komplex (egyváltozós függvény: f(z) : z -> f(z) leképezés, ahol z komplex változó, f(z) komplex értékű.
azaz z= a+ I*b alakban írható, ahol a,b valós változók.
Célszerű szerintem a függvényt is ilyen alakba áítrina, tehát valós képzetes részek összegére és így vizsgálni...
Előszőr rajzolni próbáljuk:
restart;
with(plots):
kif:=(z-I)*I/(z-1);
z:=a+b*I; # a függelten komplex változót felírjuk valós képzetes #részekre bontva
# mivel a és b itt valós és a maple alapértelmezés szerint komplex #vákltozókat #feltételez, itt móost megmondjuk neki, hog yvalósak a #és b: assume paranccsal: feltétel megadás
interface(showassumed = 0):# ez csak egy megjelenítésbeli dolog...
assume(a,real):assume(b,real);#feltételek a-ra és b-re
valresz:=Re(kif);
kepzresz:=Im(kif);
complexplot3d( [valresz, kepzresz], a = -20..20, b= -20..20,axes=boxed,title="|(z-I)*I/(z-1)|",labels=["Re(z)","Im(z)","abs(f(z))"]);
a komplex függvény abszolút értékeét ábrázolja
igazából még ezzel nem mész semmire.
Közveltnül nem lehet egy komplex függvényt ábrázolni, mert 4D kéne hozzá: x és y tengelyen re(z) és im(z) a z tengelyen lehetne re(f(z)) és a további tengelyen Im(f(z)), de ezt nem lehet, ezért a harmadik tengelyen pl. abszolút értékét f(z)-nek, vagy valós részét avgy képzetes részét vagy szögét lehet ábárzolni.
-
 #180
#180
:))
köszi
most azt próbáltam, hogy
plot(2+4*I);
Plotting error, empty plot
vagy ez így hülyeség? -
xDJCx #179 Így van. A kis i az egy változó, ha nincs megadva érték neki, nem tud vele mit kezdeni a maple. Ezéret marad kiértékeletlenül a Re(i). I (nagy i) ez a képzetes egység azaz a gyök(*1). A nagy i helyett lehetne sqrt(-1)-et írni.
Mindjárt megnézem a függvényt, így már értelmes a feladat. -
 #178
#178
Re(2+4*I);
= 2
Re(2+4*i);
= 2+4*Re(i)
Mi a különbség a kicsi i és a nagy I között?
Mert látom, van. :)
A kicsi i az egy változó?
A nagy I, meg ami "nekem kell"? :) -
 #177
#177
el, szorri
[zéminuszegy]
(z-i)i/(z-1) -
xDJCx #176
Ez így nem stimmel, nézd meg jobban, tényleg ez a feladat? (z-i)*i/(z-i) i-re egyszerűsíthető, ha z<>i, úgyhogy ez nem lehet valós! Szerintemel elnéztél valamit. -
 #175
#175
és erre gondoltam, hogy akkor esetleg ha megpróbálom kirajzoltatni maple-el, akkor megkaphatom az eredményt -
 #174
#174
hümm.. a pontos feladat úgy szól, hogy milyen alakzatot alkotnak azok a z pontok a síkon, amikre (z-i)i/(z-i) negatív valós szám :) -
xDJCx #173
Gondolom ez egy komplex függvény akar lenni (z -> (z-I)*I/(z-1)-való leképezés), akkor ha z=I, akkor nincs értelmezve, egyébként meg I az értéke. -
 #172
#172
hú ez nekem sötét lesz..
van egy ilyen feladat, ezt szerettem volna ábrázolni:
(z-i)i / (z-i)
Egy ilyet, hogy kell megcsinálni? -
xDJCx #171 Szia!
Pl.
z1:=2+4*I;# képzetes egység az I
Re(z1); # pl. z1 valós része
Im(z1);# képzetes rész
abs(z1);# nagysága
argument(z1); # szöge radiánban
evalf(argument(z1)); # lebegőpontos számként...
evalf(convert(argument(z1),degrees));# fokban a szög
conjugate(z1);# konjugáltja
# Pl. Két komplex szám és különbségük ávrázolása:
z1:=2+4*I;#
z2:=5+6*I;
z3:=z2-z1;
with(plots):
# vektorok rajzolása : arrow(<x,y>) :a 0,0, pontból x,y pontba irányuló nyilat (helyvektort) rajzol
z1abra:=arrow(<Re(z1),Im(z1)>, shape=arrow,color=red,head_length=0.3,head_width=0.2):
z2abra:=arrow(<Re(z2),Im(z2)>, shape=arrow,color=blue,head_length=0.3,head_width=0.2):
# a z3-hoz: arrow(<x1,y1>,<dx,dy>...)-vel: x1,y1 pontból dx ,dy irányba rajzol vektort:
z3abra:=arrow(<Re(z1),Im(z1)>,<Re(z3),Im(z3)>, shape=arrow,color=maroon,head_length=0.3,head_width=0.2):
display(z1abra,z2abra,z3abra);
#( lehet komplex függvényeket is ábrázolni: ?complexplot ) -
 #170
#170
Sziasztok!
Valaki tudna segíteni, hogy komplex számokat hogyan lehet (ha lehet) ábrázolni (kezelni) Maple-ben?
Köszi! -
xDJCx #169
Itt néhány rajzolási- és koordinátageometriaiometriai példa található a maple-hez magyarul:
http://www.bgrg.sulinet.hu/tanarok/tanweb/MOROCZL/maple/index.htm -
 #168
#168
hümm...
e héten már volt egy analízis gyakorlatom meg egy előadásom :)) -
xDJCx #167
Néhány ingyenes csomag a maplehez:
- share library: jónéhány kisebb-nagyobb csomagot tartalmaz a maplehez (
a maplesoft oldaláról vagy innen letölthető: http://myweb.tiscali.co.uk/maplenut/
- advisor csomag: több új/javított maple-parancs, maplehez tanácsok stb...
http://www.math.ubc.ca/~israel/advisor/advisor6/advisor6.html
- szimbolikus áramköranalizis: Syrup
innen letölthető: http://www.k-online.com/~joer/syrup/syrup.html
(AC, DC, tranziens analizis, szimbolikus formában, azaz elő lehet vele állítanipl. az átviteli függvényt analitikus formában. Netlistes formában lehet vele az áramkört megadni. Csak kisebb áramkörökre jó, nincs alkatrészkönyvtára, létrahálózatokat lehet csak felrajzolni vele.)
- qft: kvantumfizikához csomag
http://www.scg.uwaterloo.ca/~ecterrab/qft.html
- Maple-PVs interface
Matematikai tételek, állítások gépi bizonyítására (automated theory proving) szolgáló önálló PSV programhoz készült Maple-interfész. Kell hozzá persze az eredeti progi is, ahhoz úgy néz ki Windows alatt nem fut, linux kell hozzá.
Pl. azonosságok igazolására, függvény folytonosság eldöntésére stb... ( a maple nem megbízható ebben),
a program: http://www.dcs.qmul.ac.uk/~hago/Maple-PVS/
egy publikáció róla: http://www.csl.sri.com/users/owre/papers/tphols01/tphols01.pdf#search=%22pvs%20maple%22
-
xDJCx #166
Dos-os maple demo, 1991-ből itt:
http://www.mapleprimes.com/blog/tom_4/functioning_maple_v_r1_dos_demo_circ_1991 -
xDJCx #165
Maple-hez bevezető előadások itt is:
http://rs1.sze.hu/~horvathz/gyak1.txt
http://rs1.sze.hu/~horvathz/gyak2.txt
http://rs1.sze.hu/~horvathz/gyak3.txt
http://rs1.sze.hu/~horvathz/gyak_fvgraf.txt -
xDJCx #164
Üdv!
Tényleg jó tanáraid voltak neked ezek szerint, sajnos az én tanáraim nem értettek nagyon a Maple-hez...
Nem ismerem az említett tanárokat személyesen, de a Maple-t a Molnárka-féle könyvből kezdtem el jó pár éve tanulni és nagyon szerettem ezt a könyvet.
Ez az a könyv a többi magyar nyelven megjelent könyvvel együtt:
Molnárka és szerzőtársai: A Maple V. és alkalmazásai, Springer, 1996
Klincsik M. és Maróti Gy. : Maple 8 tételben, Novadat, 1995
Heck A. : Bevezetés a Maple használatába, JGYF Kiadó, Szeged, 1999
Az említetten kívül még a Heck könyvet olvastam, az is nagyon szuper, csak mint a többinek az a problémája, hogy régiek, azóta sok mindenben változott a Maple, De ezzel együtt is nagyon ajánlom őket.
A hivatkozott Maple-anyagok is szuperek, azért kár, hogy nem frissítik őket, hiszen 5-6 évesek. (Pl. azóta a Maple a %, %%, %%% -ot használja a korábbi eredményre való hivatkozásra a ", "", """-helyett, vagy már ez E nincs lefoglalva az exponenciális állandóra, és persz új parancsok, módosított prancsok, sok új programcsomag, stb...).
-
nksiker #163 Az alább olvasható hivatkozás a matektanáromé:
(1) http://rs1.szif.hu/~molnarka/ANALIZIS/
(2) http://rs1.szif.hu/~molnarka/LINEARIS_ALGEBRA/
Nagy élmény volt számomra a Maple-lel tanulni a matematikát. Felejthetetlen volt e két tantárgyból a vizsgai is, hát sokan el is véreztek, de én nem :)
Azóta rendkívül sok mindenhez tudtam használni, amúgy közgazdásznak tanulok...
Nagyon sokat köszönhetek dr. habil Molnárka Győzőnek és Miletics Editnek.
Amúgy az érdeklődőknek ajánlok még egy honlapot, az is rendkívül jó és hasznos. Szintén az egyik tanáromé (Kallós Gábor dr. PhD), csak ő számtechet tanított, de a mi egyetemünk széles oktatási spektruma rendkívüli lehetőségeket kínál... :)
(3) http://rs1.szif.hu/~kallos/maple/
Remélem mindenki jól tudja hasznosítani a linkeket.
Üdv:
nksiker
SZE - Győr - www.sze.hu
-
xDJCx #162
Alapvető Maple parancsok, használat magyarul:
http://files.szt.ektf.hu/dl.php?file=files%2FTan%E1ri+megoszt%E1sok%2FHolov%E1cs+J%F3zsef%2Fnumer%2F11-Maple.pdf -
 #161
#161
vov -
xDJCx #160
Analizis és lineáris algebra előadások Maple-vel:
http://rs1.szif.hu/~molnarka/ANALIZIS/
http://rs1.szif.hu/~molnarka/LINEARIS_ALGEBRA/ -
xDJCx #159
Itt néhány koordinátageometriai stb. matek-feladat Maple megoldása található :
http://www.sulinet.hu/tart/cikk/Raf/0/17445/1 -
xDJCx #158 Egy másik meoldás, a geometry csomag parancsait felhasználva:
restart;
with(geometry):
line(e1, y = 2*x+3, [x, y]):
line(e2, y = 3*x+9, [x, y]):
circle(kor, x^2+y^2 = 25, [x, y], 'centername' = o):
draw([e1(color = blue), e2(color = red), kor(color = green, printtext = true)], view = ([-15 .. 15, -15 .. 15]), axes = normal);
lásd a helpben: ?geometry
-
 #157
#157
hümm.. pedig mivel én is most kezdtem, szerintem tök lökötten írtam be mindent
kérdeztem valamit, majd ha megvolt az eredmény, akkor beírtam ide, hogy mit csináltam, hogy ez lett -
xDJCx #156
Be kell másolni az egyes sorokat a MAplebe egy-egy parancssorba. A Maple 10-ben ehhez például nyom az ember egy [> -gombot (felül) így csinál egy parancsbeviteli sort, ide kell egy sort bemásolni.
Még meg lehet próbálni a Maple 10-ben a Toolsban Assitantok közül a plot buildert. Azzal is lehet több diagramot egy ábrába rajzolni, de nyilván nem olyan rugalmas mint kódolni.
A Maple elsősorban egy matematikai programnyelv, még akkor is ha 10-esben jelentős lépéseket tettek a felhasználóbarátabb, egerezős-kattintgatós-kódolás nélküli használat afelé (lásd Matchad). Ha viszont igazán rugalmasan szeretné az ember használni a Maple széleskörű lehetőségeit, akkor kénytelen elmélyedni a helpben, mondjuk ehhez persze kell az angol tudás. Persze nem kell mindent paraméterezést fejből tudni, elég ha gyorsan tud az ember a helpben kereseni... -
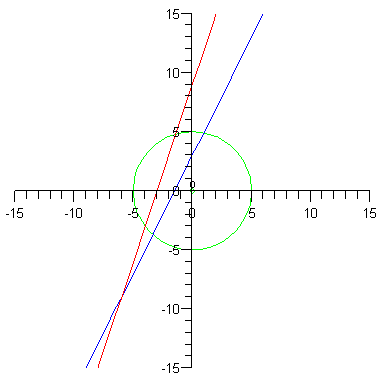
xDJCx #155 Többféleképpen is lehet, egy megoldás (Maple 10 worksheetben):
restart:
#szukseges rajzolo csomagok betoltese:
with(plots): with(plottools):
#egyenesek es a kor kepletei
e1 := 2*x+3;
e2 := 3*x+9;
kor := x^2+y^2 = 25;
# felirat hozzajuk: stringbe konvertalva a kepleteket
e1felirat := convert(y = e1, 'string'):
e2felirat := convert(y = e2, 'string'):
korfelirat := convert(kor, 'string'):
# az egyenesek , a kor es a feliratok abrait kulon elkeszítjuk:
abra1 := plot(e1, x = -15 .. 15, y = -15 .. 15, color = blue):
abra2 := plot(e2, x = -15 .. 15, y = -15 .. 15, color = red):
# implicit figgveny rajzolasa: (implicit, azaz nincs y kifejezve...)
abra3 := implicitplot(kor, x = -15 .. 15, y = -15 .. 15, color = green):
# ez lesz akor kozeppntja:
abra4 := disk([0, 0], .2, color = green):
# szovegek abrakba:
abra5 := textplot([6, 10, e1felirat]):
abra6 := textplot([-3, 8, e2felirat]):
abra7 := textplot([6, 5, korfelirat]):
# a display utasítassal egyszerre rajzoltatjuk ki oket:
display([abra1, abra2, abra3, abra4, abra5, abra6, abra7], scaling = constrained);
( : -vel zárva a sorokat nem írja ki az eredményt.)
Az egyes parancsok részelteit a helpben érdemes megnézni: ?parancs
-
manwe #154 igen, természetesen megnéztem az oldalt, és láttam is ezeket, de nekem ez kb. mintha kínaiul lenne, az egész parancssort be kell írnom? nem lehet vhogy ezt egyszerűbben? -
 #153
#153
szerintem erre lejjebb van példa - talán még ezen az oldalon.. -
manwe #152 meg az is érdekelne, hogy pl. hogy lehet odaíratni a szöget amit bezárnak az egyenesek az x tengellyel, tegyük fel h ezek alpha meg beta, akkor ezt hogy lehet odaírni? -
manwe #151 én még grafikont nem készítettem mapleben, és ezért esetleg ha vkinek van ideje elmagyarázná nekem, hogy hogy lehet ilyet csinálni? pl ha akarok rajzolni két egyenest, mondjuk legyen y=2x+3 meg y= 3x+9 és még szeretnék egy kört is, aminek az egyenlete: x^2+y^2=25, akkor hogy lehet megcsinálni azt, hogy ez egy grafikonon legyen(mert külön-külön megy) és még azt h az egyenesekre oda is írja h ennek ez meg ez az egyenlete, meg mondjuk megjelenítse a kör középpontját szinessel. Ha vki esetleg ráérne válaszolni, azt megköszönném. -
manwe #150 nincs meg vkinek véletlenül a 10.04, vagy nem tudjátok h honnan lehetne letölteni? -
xDJCx #149 Munkahelyi példány. Meg van hozzá egy-két fizetős csomag is (pl a Global Optim.. Toolpack: ez egy nemlineáris, többváltozós globális min., max kereső. Kifinomultabb mint a Maple beépített Optimalizációs csomagja, mert az lokális max., mint tud keresni stb...).
Adnak a Mpalehez hozzá több kézikönyvet is, elég jók, nagyon ajánlom mindenkinek ezeket, és szerencsére le lehet tölteni őket ingyenesen a maplesoft oldaláról (pdf-ek), esetleg valamelyikhez regisztrálni kell magadat de ez nem termékregisztráció, nem kérnek hozzá semmi kódot stb. Meg hasznos a quick refencia card is, ez is letölthető. (Ha kell valakinek el tudom emailezni pdf-ben őket.) -
manwe #148 hát ez nagy hátrány, te neked honnan van meg az eredeti? megvetted, vagy egyetemen adták? -
xDJCx #147 Most tettem fel a 10.04-est, és abban egyből megjelent
egy Accents paletta is, amin van vektornyíl, szóval ezzel egy mozdulattal lehet vektoros jelölést csinálni. Mintha ilyen paletta nem lett volna a 10-esben, pedig kerestem.
(a mininovás 10-essel nem fut az upgrade, nem érdemes letölteni!) -
manwe #146 xDJCx-nek köszönöm a segítségét, az volt a gond, hogy nem volt benn a layout paletta, és emiatt nem találtam, most már mennek a vektornyilak is:D. kösz szépen