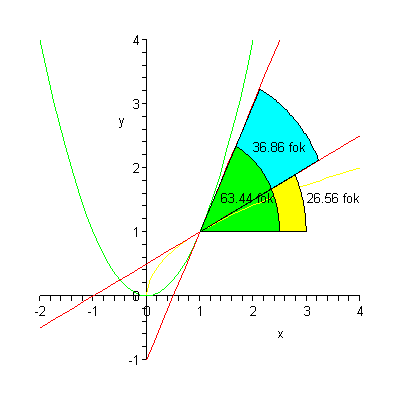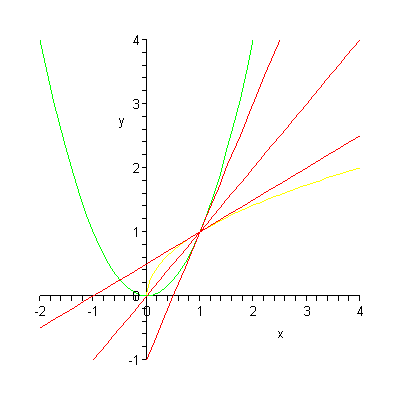625
A Maple egy fejlett matematikai problémamegoldó és programozói szoftver.
-
 #145
#145
vegyél table PC-t
(Minden Tájváni kölöknek olyan van az iskolában) -
manwe #144 hm, még mindig gondolkodok, hogy vajon megéri e maple-lel jegyzeteket csinálni:D, mert vhogy sokkal jobb(annak aki úgy szereti a gépét mint a hegedűs a hegedűjét..:D) géppel csinálni, csak nem tom h hosszabb lenne e. Eddigi próbálkozásaim során, vmibel lassabb ha képleteket, számításokat kell írni, de ha vmi szöveg van(pl. indoklásként) akkor sokkal gyorsabb(világos mivel a gépelés alapból az), szóval nem tom eldönteni h mit csináljak..:S -
xDJCx #143 Vagy így is lehet pl. x fölé:
x [Ctrl][Shift]["] then insert symbol, e.g. from Arrows palette...
(Maple 10 Quick reference)
-
xDJCx #142 A Maple 10-ben a Layout palettán van olyan szimbólum, ahol valami fölé írható egy másik valami. A felső nyílhoz pedig az Arrow palettán található nyíl.
Ha mondjuk nem egy karakter fölé kell a nyíl, pl. AB fölé, akkor egybe kell kijelölni őket először.
(Ha nem látszana valamelyik paletta, akkor a View - Palettes - Arrange palettes-ben a bal oldali Dock areas-ba kell húzni felülről.)
Lehet másképp is vektornyílat csinálni, de az elég körülményes.
Igazából ez nem kényelmes a Maple-ban, én nem szoktam használni. -
manwe #141 az lenne a kérdésem, hogy a vektor jelet hogy lehet létrehozni, pl. AB és akkor felette a nyíl, mert én sehol sem találtam
ha valaki tudja, kiváncsi lennék rá
előre is kösz -
xDJCx #140 Az upgradeket persze érdemes a korábbi verzókhoz is letölteni. A 9.5-höz van pl. a 9.5.2-es. -
manwe #139 kár pedig igazán jó lett volna, ha géppel lehetett volna jegyzetelni:( -
xDJCx #138 Ejnye, méghogy letölteni!
Egyébként ha már letöltötted, akkor mindenképpen érdemes a friss patchet is letölteni a maplesoft oldaláról. Most a 10.04-nél tartanak, a 10.03-ban még volt (legalább) egy súlyos bug.
Nem javasolnám jegyzetelésre. Ahhoz tényleg gyorsnak kéne lenned! :)
-
manwe #137 A Maple 10-et a http://www.mininova.org/ oldalról lehet letölteni, torrentes és én bitcometet használtam a letöltéshez, ami a www.bitcomet.com-ról tölthető le.
kérdésem lenne bár én még csak középiskolás vagyok, de jövőre érettségizek, hogy ezt a programot lehet e használni előadáson történő jegyzetelésre? tehát lehet e olyan gyors mint a toll és papír?
előre is köszönöm -
xDJCx #136 exp(1);
evalf(%); -
 #135
#135
Hogy kell felírni az e-t?
mármint nem kiírni, hogy e.
Gondolom van egy ilyen objektum. -
xDJCx #134 Igen, elég viszonylag rövid a kód, a nehézség csak az, hogy mivel baromi sokat tud a Maple, sok parancs és mindenféle boynolult paraméterezés, ezt csak a helpből lehet kibogarászni, mert persze egy MAple könyvben sem lehet benne minden. Ráadásul a Maple könyvek hamar elavulnak. -
xDJCx #133 Az a 26,6 fok = 0,46 rad = arctan(1/2) -
 #132
#132
a sárga szög az = arctg mennyi? -
 #131
#131
Eeez igen!
Te nagyon nagyon vágod ezt!!! :)

De azt jó látni, hogy igazából a kótmennyidéget tekintve nem is kell annyi kód, hogy mindezt megcsinlja.. és ez tök jó
Ja, és köszönöm szépen! :) -
xDJCx #130 Kiegészítés:
Most a szögeket is berajzoltam, ha valaki ilyesmit szeretne Maple-ban csinálni:
restart;
with(Student[Calculus1]):
with(plots):
f1:=x->x^2: # függvény definíciók
f2:=x->sqrt(x):
a:=1: # x=a helyen nézzük
m1:=eval(diff(f1(x),x),x=a):# meredekség: derivált x=a helyen
m2:=eval(diff(f2(x),x),x=a):
m1szog:=evalf(arctan(m1)):# radianban az érintők szöge
m2szog:=evalf(arctan(m2)):
deltaszog:=evalf(m1szog-m2szog): #az érintők különbségi szög
a1:=Tangent(f1(x), x=a,output = line):# az erinto egyenlete f1-re
a2:=Tangent(f2(x), x=a,output = line):#az erinto egyenlete f2-re
ab1:=plot(f1(x),x=-2..4,y=-1..4,color=green):ab2:=plot(f2(x),x=-2..4,y=-1..4,color=yellow):# függvényábrák
ab3:=plot(a1,x=-2..4,y=-1..4,color=red):ab4:=plot(a2,x=-2..4,y=-1..4,color=red):# érintőábrák
# szögívek:
m1szogab := plottools[pieslice]([a,f1(a)], 1.5, 0..m1szog,color=green):
m2szogab := plottools[pieslice]([a,f1(a)], 2, 0..m2szog,color=yellow):
deltaszogab:=plottools[pieslice]([a,f1(a)], 2.5, m1szog..m2szog,color=cyan ):
# szög értékek fokban, sztringbe konvertálásuk felirathoz
m1szogszov:=cat(convert(evalf(m1szog*180/Pi,4),'string')," fok"):
m2szogszov:=cat(convert(evalf(m2szog*180/Pi,4),'string')," fok"):
deltaszov:=cat(convert(evalf(deltaszog*180/Pi,4),'string')," fok"):
# feliratok az ábrára: szögértékek
m1szogtxt:=textplot([1.4,1.4,m1szogszov],align={ABOVE,RIGHT}):
m2szogtxt:=textplot([3,1.4,m2szogszov],align={ABOVE,RIGHT}):
dszogtxt:=textplot([2,2.2,deltaszov],align={ABOVE,RIGHT}):
# együtt kirajzolni az ábrákat:
display([ab1,ab2,ab3,ab4,m1szogab,m2szogab,deltaszogab,m1szogtxt,m2szogtxt,dszogtxt]);
-
xDJCx #129 Jó, akkor elárulom, én is abban rajzoltam az ábráimat. Képzelheted mennyi munka van benne! Szerencsére a síkképernyőmön könnyű volt szöget mérni a kis műanyag szögmérőmmel! :D -
xDJCx #128 Egy kis Maple történelem:
Az úriember a Maple egyik alapítója:
Dr. Keith Geddes
Keith Geddes:
"Initially, Maple was implemented in B on a Honeywell computer, but soon afterward, C became the obvious widely available language. In 1981, we moved from the Honeywell to a Vax 780. We purchased our first UNIX box for Maple in 1983 for $25,000, a Spectrix computer with one megabyte of memory.
... By the first week in December 1980, we had an operational Maple system, and it evolved from there. In trying to name the system, we started thinking of an acronym. When I suggested the name "Maple," we decided we would go with that, as it seemed like a good Canadian name (not an acronym).
... "
-
 #127
#127
:DDD
persze
C:\WINDOWS\system32\mspaint.exe :D -
xDJCx #126 Egyébként jó kis rajz, megadod a kódot? :) -
 #125
#125
akkor jó, én is így gondoltam -
xDJCx #124
Nem stimmel. A berajzolt szög 63 fok körül van, előbb ki lett számolva, a keresett szög pedig 37 fok körül, szóval nem a fele. -
 #123
#123
igen, tom hogy nem jó
de akkor az igaz, hogy.. vájá, mutatom
enenk a szögnek (kék) a fele a nekünk kellő szög?
mert szerintem annyira nem, de a tanár azt mondta -
xDJCx #122
Szóval a középső egyenes lenne a 45 fokos, hát az nem az érintő!
-
xDJCx #121
Sajna az nem stimmel :( . Az m2szog a y=gyök(x)-hez tartozik, a gyök(x) deriváltja
1/(2*gyök(x)), ez az x=1 helyen = 1/2 értékű. Az érintő meredeksége (m) ezért 1/2. Az érintő egyenlete pedig y= 1/2x + 1/2. Ennek megfelelő szög nem lehet 45, mert az pl. éppen y=x+b, vagy y=x egyenletű egyenesnek lenne, tehát aminek a meredeksége 1. Szóval 45 fokos a sima y=x egyenes . -
 #120
#120
hümm..
nekem m2szog-re 45 fok jött ki a dogában -
xDJCx #119
Jó, csak az egyik függvényt rajzoltam ki az előbb az egyszerűség kedvéért, de azt számoltam ki kértél, az érintők közti szöget.
Itt a teljes ábra, most gifben mentve, és az ábra kódja:
restart;
f1:=x^2:
f2:=sqrt(x):
a:=1: # x=a helyen nézzük
with(Student[Calculus1]):
with(plots):
a1:=Tangent(f1, a,output = line):# az erinto egyenlete f1-re
a2:=Tangent(f2, a,output = line):#az erinto egyenlete f2-re
ab1:=plot(f1,x=-2..4,y=-1..4,color=green):ab2:=plot(f2,x=-2..4,y=-1..4,color=yellow):# a függvények ábrái
ab3:=plot(a1,x=-2..4,y=-1..4,color=red):ab4:=plot(a2,x=-2..4,y=-1..4,color=red):# az érintők ábrái
# külön lett előállítva a négy ábra, és a végén együtt kirajzolni őket.
display([ab1,ab2,ab3,ab4]);
-
 #118
#118
hátöö, igen, valami hasonló :)
A piros egyenes és a sárga görbe x=1-beni érintőjegyenesének a szöge.
ez rosszabb minőségű kép, mitn amit én csináltam :P -
 #117
#117
sry, nem is képet tettem be, csak ezt a sort
plot({x^2, (x-2)^2, (2*x)-1, (-2*x)+3}, x=-2..4, y=-1..4); -
xDJCx #116 Az első ábra:
-
xDJCx #115 Ha jól értem:
restart;
f1:=x^2;
f2:=sqrt(x);
a:=1; # x=a helyen nézzük
# az érintő meredeksége a derivált értéke az adott pontban:
m1:=eval(diff(f1,x),x=a);# deriválni és kiértékelni az adott helyen
# a másik függvényre is:
m2:=eval(diff(f2,x),x=a);
m1szog:=evalf(arctan(m1)*180/Pi);# fokban legyen a szöge
m2szog:=evalf(arctan(m2)*180/Pi);
deltaszog:=evalf((m1szog-m2szog));
# még ez is kipróbálható:
with(Student[Calculus1]):
Tangent(f1, a,output = line);# érintő egyenlete (első függvényé)
Tangent(f1, a,output = plot);# felrajzolni a függvényt és érintőjét
Tangent(f2, a,output = line);# másik függvényre is
Tangent(f2, a,output = plot);
-
 #114
#114
Hümm..
Akkor van egy aktuális "probléma". Analízis.
Pl van egy x^2 és egy gyök(x) fv.. és ezeknek kell meghatározni pl az x=1-ben a két érintő által bezárt szöget
gondolom ennek megoldására van egy kb 3 soros megoldás :)
lejjebb én már csináltam és képet is tettem be az x^2 és a (x-2)^2 -ről.
Mert ugye itt a megoldás az alfa = arct 2, ami valami ~64,... lesz. Mármint ez kétszer. -
 #113
#113
:D
Lebuktam h printszkríneltem? :D -
xDJCx #112 Egy kis kiegészítés: ki lehet irattatni a felrajzolt objektumot adatait, pl. a körülírt kör egyenletét, vagy a magasság-vonalak egyenleteit is: a detail() utasítással:
restart;
with(geometry):
triangle(T, [point(A,-1,1.5), point(B,1,1), point(C,0.5,2.5)]):
circumcircle(Elc, T, 'centername' = O):
altitude(hA1,A,T):altitude(hA2,B,T):altitude(hA3,C,T):
draw([Elc(color=blue),T(color=red),hA1(color=green),hA2(color=green),hA3(color=green)],printtext=true);
detail(T);detail(Elc);detail(hA1);detail(hA2);detail(hA3); -
xDJCx #111 Egyébként az ábrán állva (Mapleban) a jobb clickre előjövő menüben le lehet szedni a keretet (Axes ---> None). A menüben exporttal pedig pl. jpegben elmenthető. -
xDJCx #110 shift enter
> Így kezdődnek a parancssorok, a szögletes zárójel a sor elején egy végrehajtási egységet jelent. -
 #109
#109
draw* -
 #108
#108
Ahaam, először definiáljuk a 2+3 objektumot, majd a drow-val kiíratjuk.
És így lesz belőle ez:
Csak, mert lehet, h mást is érdekel -
 #107
#107
Monnyuk nekem a háromszög + körülírható kör + Simson egyenesek kellettek.. de már levizsgáztam. :) -
 #106
#106
olyan sorugrást hogy cisnálsz, hogy nem kezd olyan új "bekezdést"?
Vagy hogy van ez? Mit jelent a ">"?
És mit a sor eleji "kapocs"?