1398
-
HUmanEmber41st #1235 Heisenberg előtt akkor nem is volt véletlen?
Na jó, nem forgatom ki a mondanivalódat:D. Ha Heisenberg bebizonyította, h van véletlen, akkor semmi baj.
Tehát a lenti miértekre a tudományos válasz röviden:
mert csak.
Akkor végül is egy pontnál tovább nem is illik tovább kérdezősködni,(miérteket kérdezni) mert a tudományos indoklás: így alakult és kész, ez van, ezt kell szeretni. Akkor mégis mit kutat az a sok fizikus, matematikus, csillagász és egyéb kenyérpusztító? Minek kutatnak, hiszen a válasz már Heisenberg óta létezik... -
 #1234
#1234
Ez HÁBORÚ! Háború meg nem fair.
Legalábbis _nekik_ háború, nem értik meg, hogy a tudomány nem hatalommal, nem erővel működik... -
#1233
amúgy meg nagyon könnyű megválaszolhatatlannak tűnő kérdéseket
feltenni, és egyáltalán "nem fair" :PP
ha majd egy szuperintelligens létforma leszünk (ha addig nem irtjuk ki
magunkat az ilyenek miatt mint te:P) akkor is rengeteg kérdés ott lesz
még, a régiek megoldódnak, jönnek újak -
#1232
Heisenberg óta tudjuk hogy véletlenek vannak
a mi a tömeg kérdésre meg remélhetőleg 1-2 éven belül jön a válasz:)
(Higgs mező:) -
#1231
a fizikai törvények az ősrobbanást szempillantásnyira követően "fagytak be", lehet véletlen műve is, de nagyon kicsi az esély..ha véletlen lett volna akkor a multiverzum elmélet az igaz...
a tér meg létezik, az univerzum nem egy ürességbe robbant bele
hanem vele maga a tér terjedt ki, illetve a 3ik dimenzió.
Einstein-nek meg még a legnagyobb tévedéséről is kiderülhet hogy igaz..
sötét energia..
-
 #1230
#1230
Igen,látszólag akár véletlennek is mondható. a fizikai törvényeket és konstansokat az univerzum kezdeti feltételei határozzák meg. ezeket a kezdeti feltételeket nem ismerjük. az elméletek nem írják le őket. nem tudjuk ki állította be azokat és miért pont úgy ahogy. akár másmilyen törvények és konstansok is jellemezhetnék az univerzumunkat,látszólag véletlen az egész, DE!
az belátható, hogyha pl. az elektron tömege nem annyi lenne amennyi, a fény sebessége nem annyi lenne amennyi, vagy a univerzum átlagsűrűsége nem annyi lenne amennyi,vagy egyáltalán nem olyanok lennének a törvények, amilyenek, akkor nem alakulhatott volna ki a mi létünkhöz megfelelö univerzum (mert például ha sűrűbb lenne az univerzumunk már nagyon hamar öszzehúzódott volna ha pedig csak egy kicsit is ritkább, akkor meg már rég teljesen üres és kihűlt lenne ). tehát igencsak kevés fajta univerzum létezik, amelyben mi létezhetnénk a konstansok és fizikai törvények szempontjából. ilyen módon egyáltalán nem véletlen h az univerzumunkat éppen olyannak figyeljük meg, amilyennek. (ezt a gondolatmenetet egyébként antropikus elvnek hívják) -
HUmanEmber41st #1229 Tudom, h nem lehet megfigyelni közvetlenül semmit.
Mindenre csak következtetni lehet.
Sejtések, elméletek.
Szerinted a filozófia tudományának kell foglalkoznia a lentebb leírt kérdésekkel, vagy megteszi a fizika is?
A miértekre végül is ki kutatja, kutathatja a választ???
Tehát, tudjuk, h ilyen.
De MIÉRT ilyen, miért annyi és nem több, vagy kevesebb?
Véletlenül így alakult?
Sztem a véletlen nem tudományos érv, vagy bizonyítás. -
 #1228
#1228
persze, szabad szemmel. a baktériumokat is onnan tudjuk h szabad szemmel látjuk. 
a kérdésediből látszik h nem érted mit is jelent az a fogalom h fizikai elmélet. hadd magyrázzam el. az elméletek eképpen keletkeznek:
1. megfigyelünk bizonyos jelenségeket: jelenség1, jelenség2, jelenség3,..stb.
2. ezután kitalálunk ún. elméleteket. ezek arra vannak h leírjákezeket a jelenségeket, ami annyit jelent egy elmélet akkor jó ha helyesen jósolja meg a jelenségeket, amiket megfigyelünk.
namármost az elméletek nem arra vannak h válaszoljanak olyan filozofikus jellegű kérdésekre h "miért létezünk?" vagy "mi a fény?" "mi a gravitáció". ha az elmélet helyesen írja le a azokat a jelenségeket amiket tapasztalunk, és helyes előrejelzéseket ad a kísérleteknél, akkor az tökéletesen elég.tehát ha azt mondjuk h a fény hullámrészecske,akkor mit akarsz azonkívül? a magerőt leíró elmélet leírja a nukleonok kölcsönhatását. mi az hogy "és?". mi kell ennél több?
a fénysebebesség értéke pedig egy konstans, azaz egy állandó, ami az univerzum tulajdonsága, tehát nem következhet az elméletből. az csak egy megfigyelt tulajdonsága az univerzumnak.
ilyen, hogy a hasonlót a hasonló vonzza, ez végképp szubjektív és tudománytalan megnyilvánulás. szerintem meg az ellentétek vonzzák egymást. na?
az ősrobbanásról megy annyit h nem úgy kell pontosan elképzelni, mint mondjuk egy gránát szétrobbanását. ott nem hatott (és most sem hat) semmilyen erő. -
HUmanEmber41st #1227 Megfigyelték szabad szemmel a kvantum-párok keletkezését?
Amit A. Ei. mond, annyi igaz, h fizikai test nem tud fénysebességnél gyorsabban haladni.
Hol van az a "tér", ami a bannerban is szerepel bal oldalon?
Az sem létezik, csak mint fogalom.
Mi a fény? (azonkívül, h foton, meg hullám, meg részecske)
Miért pont annyi a fénysebesség vákuumban?
Mi a gravitáció?
Mi tartja egyben a protont és a neutront? (mag-erő ezt is tudjuk.és???)
Miért vonzzák egymást az ellentétes töltések, holott a logikus az lenne, h hasonló a hasonlót vonzza?
Miért semleges a neutron, az ugyanakkora proton miért töltött?
Mi volt az az erő, ami szingularitássá préselte a világegyetemet?
Miért szűnt meg? ( és robbanhatott ősit a Világegyetem)?
Kérdések kérdések... -
 #1226
#1226
te beteg vagy? a föld laposságát nem támsztják alá a megfigyelések. -
Albertus #1225 Majd akkor érvelj a 100 évvel, ha elfogadtad a 3000 éves tant a föld laposságáról! -
 #1224
#1224
szinte hihetetlen hogy száz év után még mindig vannak akik nem egyszerűen nem fogják fel hogy megfigyelések sorát magyarázza az elmélet. valóban el kell olvasni ami a kép felett van, de nem uwunak, hanem neked. -
Albertus #1223 Te offolsz!
A topic arról szól, hogy:
"Miért nem fér öszze a Relativitás elmélete a Kvantum elmélettel? "
Olvasd el! A képek felett megtalálod!
A relativitás elmélet kamu téridőről szól, nem létező kontrakcióról, nem létező idődilatációról.
A kvantumelmélet pedig a valóságos energiákról, részecske tulajdonságokról szól.
Ahhoz hogy ezt megértsd, tudnod kell, hogy mennyi használható Einstein munkáiból és mi az, amit Einstein félreértett, és félremagyarázott.
Ezért kérlek inkább kérdezz és ne bírálj. -
uwu #1222 Ne offoljál 
A topik a relativitáselmélet és a kvantummechanika közti kapcsolatról szól
Nem hiszem, hogy bárkit is érdekelne, hogy miért nem érted te és a haverod a relativitáselméletet
-
Albertus #1221 Az idő? A vonat vége?
A fény a forrásától mindig c sebességgel távolodik.
Ha ez a forrás egy vonaton, repülőn vagy bárhol van, a forráshoz viszonyítottan álló érzékelővel mindig c sebességet mérhetünk.
Ha az a lámpa a vonaton van, akkor a vonattal együtt mozog a fénye is, a vonat eleje felé éppen úgy c sebességgel mint a vonat vége felé is c sebességgel.
Einstein elméletét arra a tévhitre építette, hogy a vonaton lévő lámpa fénye az állomás rendszerében is szintén c sebességgel halad.
De miután c+v és c-v lenne az állomás eleje és vége felé a fény sebessége, akkor pedig nem teljesülne, hogy minden rendszerben c sebességű, ezért úgy hitte, hogy az állomás rendszerének órái lelassulnak ( na perszee: ijedtükben) a vonat óráihoz viszonyítva,
és így más időszakasz alatt teszi meg a fény a c+v sebesség helyett c sebességgel azt az útszakaszt amit c+v sebességgel tenne meg.
Ugyanígy megint más idő alatt azt az útszakaszt amit c-v sebességgel tenne meg.
Azaz az idő relatívvá válik, előrefelé is más sebességű és hátrafelé is más sebességű. (Sőt! Mindenfelé más sebességű.)
Persze ez hülyeség, de sokan hisznek benne.
Van egy Gézoo nevű barátom, akinek egy egészen egyszerű módszere van arra, hogy tisztázzuk azt, hogy a fény merre megy.
Ugyanis ha például egy puskával meglövünk egy vonatot, akkor a vadász a sín-állomás rendszerében állva például ß szögben célozza meg a vonatot, akkor a lövés pillanatában éppen mellette elhaladó ablakon lép be a lövedék és a vonat hosszára merőlegesen a másik ablakon kilép.
Igaz, az is, hogy a vonaton lefényképezett lövedék hossztengelyén a vadász mindvégig rajta marad.
A lövedék a vonatra merőlegesen halad át a vonat rendszerén, de a hossztengelye ugyanazt a ß szöget zárja be a merőlegessel, mint a vadász puskája a vonat hossztengelyével.
-
Albertus #1219 Szia!
Örülök hogy tetszik! Egy dologra célszerű figyelni: Gézoo folyton bővítgeti, a lap bal felső sarkában van a frissítési dátum-idő.
Van amikor naponta többször kiegészíti a folytatásokkal és csak
akkor jelenik meg az új, ha F5 -öt nyomtunk. -
 #1218
#1218
köszi, ez tényleg jóóó
neki is ugrok (: -
Albertus #1217 Érdekes weblapra bukkantam: gezoo.fw.hu
Ha a kollégának igaza van, akkor csupán látszatot ír le az Einstein féle relativitás.
Nagyon meggyőző, mégis egyszerű, érthető a bizonyítása.
Tud valaki érvet a levezetése ellen?
Kis ízelítőnek lementettem két egymással Einstein szerint egyenértékű
jelenség animációját.
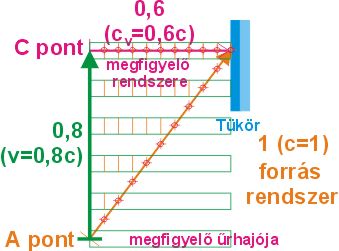
Az egyiken egy villanást követően a lámpától távolodó rendszerben
látjuk hogy a fényről miért hiszi a lámpától távolodó, hogy a saját rendszere Y tengelyén halad. Persze így a távolodót rövidültnek és lassultnak látja:
A másik ugyanezt mutatja a lámpától távolódó szemszögéből.
Ő úgy látja, hogy a lámpás rendszer tőle -x irányban x= -0,8ct függvény szerint haladva azt hiszi, hogy a lámpájától halad a tükör felé a fény.
Ő viszont a lámpájával száguldozót felgyorsúltnak és megnyúltnak látja.
Melyiküknek lehet igaza?
-
Albertus #1216 :) Vicces vagy!
A rövidülés csupán látszat! Egyetlen oka a fény véges és állandó
haladási sebessége a térben.
Ha egy rendszerből egy megfigyelőt indítunk útra, kezében a rendszer hiteles méterrúdjával, akkor ez a megfigyelő azt fogja tapasztalni, hogy amikor sebessége a nyugvó rendszerhez relatívan pl. v=0,8c
akkor a rendszerben maradt méterrúd hossza csupán 0,6-od része
a kezében tartott méterrúddal.
És csak a nagyon hülye megfigyelő hinné azt, hogy a nyugvó, változatlan rendszer csupán attól, hogy Ő a megfigyelő eljött onnan
"bánatában" összezsugorodott volna!
Nem! A nyugvó rendszer hosszai nyugalomban vannak. Változatlanok.
Még akkor ha a nyugvó rendszerből előbb elindult megfigyelő
méterrúdját a forrás rendszerből nézve megrövidültnek látjuk, akkor
talán hihetnénk, hogy attól mert felgyorsult v sebességre a méterrúdja
lerövidült.
Hihetnénk, ha nem lenne egy fényórája amit Einsteintől kapott.
Ezen jól látható, hogy a v=0,8c sebességgel halad a megfigyelő űrhajója
a zöld vektor irányába, a narancssárga vektor irányába egy tükör felé elinduló fény 10 db hullámát a megfigyelő rendszerében is 10 db hullámnak tapasztalja.
Miután két egymást követő hullám mindegyike egyenként is c sebességgel halad, így távolságuk csak akkor változhatna ha
relativ sebesség lenne köztük, de dv=c-c=0 azaz a hullámok közötti távolság állandó,
és mindkét rendszerben 10-10 db egymástól azonos távolságra lévő
hullám van.
Így a látszat ellenére a forrás és a tükör közötti távolság pontosan ugyanakkora mindkét rendszerben.
-
 #1215
#1215
Mielőtt bárki azt a téves következtetést vonná le, hogy az egész relativitás egy látszatot ír le, tisztázni kell, hogy a mozgó tárgyak valójában megrövidülnek és a mozgó órák valójában lassabban járnak. (amihez képest mozgást végeznek)
Amit kiszámoltam, az a koordináta-transzformáció háttere a Lorentz-elméletben.
Két esemény közt különböző térbeli távolságot kapunk,ha egymástól eltérő sebességgel mozgó inerciarendszerekben mérünk. -
 #1214
#1214
Nemtom hogy van-e isten, de ha létezik, akkor nagy matematikus. -
 #1213
#1213
Nem volt tisztázva, hol van az események origója. Ez bárhol lehet, én azt a pillanatot választottam, amikor áthalad a fény a lencsén. Ez lesz a (0,0) koordináta.
Ekkor a fénynek x_targy utat kell befutnia, ami miatt t=-fabs(x_targy/c) annak az eseménynek az időkoordinátája, amikor elindult a fény a tárgyról.
A tárgyak rövidülése valós, ahogyan azt a Michelson-Morley kísérletből levonható (a Lorentz elméleten belül), emiatt az események térbeli koordinátái távolabbra kerülnek egymástól. Ez a x_targy*=b;x_ccd*=b;
Emiatt a két módszer szinte teljesen egyforma, nem eldönthető, hogy a távolságok megváltozását egy látszat okozza, vagy tényleg a téridő torzul.
-
 #1212
#1212
Válasz a #1180ra, nem egészen úgy van ám, van néhány hiba a számításban.
tavolsag:5000.000000
specrel:6813.851439
foto :6813.851439
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int main()
{
double x_ccd,x2,x_targy,y,y2,y_targy,b,t,v,c,tan_a;
c=3e8; //fenysebesseg
v=c*0.3;//fotogep sebessege
x_targy=5000.0;//targy tavolsaga allo IRben (terbeli koordinata)
y_targy=100.0;//targy nagysaga, magassaga, nem koordinata
t=-fabs(x_targy/c);//ido koordinata, a fenyjel ekkor indult minusz, mert
//amikor a lencsen atmegy a targyrol indult feny az lesz a (0,0) koordinata
printf("tavolsag:%f \n",x_targy);//targy tavolsaga allo rendszerben
b=1.0/sqrt(1.0-(v*v)/(c*c));
printf("specrel:%f \n",(x_targy-v*t)*b);//Lorentz transzformacio
//megvaltozott tavolsag a mozgo inerciarendszerben a specialis relativitas szerint
x_ccd=1000.0;//ccd-lencse tavolsag, (ccd a kep keletkezesenek helye)
x_targy*=b;//a hosszak rovidultek, emiatt az esemenyek tavolsagai megnottek mozgasiranyban
x_ccd*=b;
tan_a=y_targy/x_targy;//tangens alfa, ilyen szog alatt latszik a targy allo IRben (szog tangense)
t=x_ccd/(v+c);//ido ameddig a mozgo ccd es a feny talalkozik
x2=c*t;//feny-ccd talalkozasi pont a lencsetol szamolva
//x2=x-v*t; // ugyan az a ccd mozgasabol szamolva
y2=x2*tan_a;//keletkezo kep merete /kisebb mint az allo kep /
tan_a=y2/x_ccd;// a lencse is mozog jobbra, mint a ccd, emiatt a fotogeppel egyutt mozogva a szog atan(y2/x_ccd)
printf("foto :%f \n",y_targy/tan_a);// megvaltozott tavolsag a mozgo fotogep kepe alapjan
}
-
 #1211
#1211
A refraktiv gravitációs modell hullámokkal dolgozik, emiatt beleillik a kvantummechanika matematikai formalizmusába.
-
 #1210
#1210
A részletek.
u=12;
ennyi szegmensből áll a kis körpálya, ahol az anyag c-vel halad. Lehet több is. (Minimum 4 lehet.)
A szegmensek miatt dtime-ot u darab részre kell osztani, ez lesz dtime2. Régebben emiatt hittem azt, hogy átlagot kell számolni a végén. Mostmár nem kell átlagolni, a fénysebességű vektorok közvetlenül a sebességhez adódnak vektoriálisan.
T a tangensvektor
a körpálya: position + N*dr*2.0; (N*dr*2.0 a sugár)
Ehhez jön +- N*dr, amiből két pontot kapok, ez p1 és p2.
Ezek mozognak dtime2 ideig T irányban c1 ill c2 sebességgel, ami a fény sebessége az adott térbeli ponton.
Ezután jön a tangens irány újraszámolása, végül Tc hozzáadódik a sebességhez.
-
 #1209
#1209
A refraktív gravitációs modellt az einsteini gravitációhoz illeszteni kicsit bonyolultabb lesz, egyenlőre nem meggyőző egyik próbálkozás sem. A görbült téridő egy tenzormező, nem egyszerű skalármező, mint amivel a modell jelenleg számol.
(vektorkezelés a másik topikban, minden float-ot cserélni kell float1-re )
-
 #1208
#1208
A legegyszerűbben úgy lehet fényelhajlást számolni, ha két nem túl távoli pontot ugyanazon irányba mozgatunk különböző sebességgel, és az végpontokból a tangens irányt újraszámoljuk.
Az ábrán egy zölddel rajzolt ellipszis pálya van newtoni gravitációval számolva és a hozzá, és a hozzá tartozó pályamenti sebesség görbe, és pirossal a fénytörés modellel számolt pálya.
Ja, hogy csak piros van? Persze, mivel pontosan fedi a zöldet, emiatt se a zöld pálya sem a zöld sebességgörbe nem látszik.
A lassabb fény ellenére ahogy közeledünk a tömeghez, a tér gradiense egyre nagyobb lesz, emiatt nagyobb a 'gyorsulás'. Habár egyenlőre csak sebességváltozást számol a program.
A fénytöréses modell kis körpályákat számol, mintha a test csavarvonalban mindig fénysebességgel haladna.
A modell függ a fény sebességétől, amíg a newtoni nem.Ki lehet próbálni, ha T*c*0.99-el számol a program, már jelentős az eltérés a newtoni pályától.
A newtoni szimuláció egyszerüsített, de teljesen helyes is ugyan ezt a pályát adja.Ilyen skálán nem számottevő a különbség.
typedef long double float1;
float1 g,c,m, Rs,r1,v1,scale, dr, dtime,geom_unit;
float3 position, speed;
int n;
void setup()
{
g=6.67428e-11;
c=2.99792e8;
m=1.9891e30;
dr=1e-4;
Rs=(float1)2.0*m*g/(c*c);
r1=Rs*40.0;
v1=sqrtl(m*g/r1)*0.8;
dtime=2e-7;
n=400000;
scale=400.0/r1;
position=float3((float1)r1,(float1)0.0L,(float1)0.0L);
speed=float3(v1*(float1)0.3L,v1*(float1)0.7L,(float1)0.0L);
}
void newton()
{
setup();
for(int j=0;j<n;j++) {
position=position + speed*dtime;
float1 r=sqrtl(dot(position,position));
float3 T=position/r;
float1 ac=dtime*m*g/(r*r);
speed=speed - T*ac;
float3 screen=position*scale;
pixel(500+(int)(screen.x),300+(int)(screen.y),0x00ff00);
screen.x=(float1)(j/100);
screen.y=sqrtl(dot(speed,speed))/400000.0;
pixel((int)(screen.x),900-(int)(screen.y),0x00aa00);
}
}
void refraction()
{
int u=12;
setup();
for(int j=0;j<n;j++) {
position=position + speed*dtime;
float dtime2=dtime/(float1)u;
for(int i=0;i<u;i++) {
float1 alpha=(float1)i*M_PI*2.0/(float1)u;
float3 T=float3((float1)cos(alpha),(float1)sin(alpha),(float1)0.0),N;
N.x= T.y; N.y=-T.x; N.z=0.0;
float3 p1=position - N*dr + N*dr*2.0;
float3 p2=position + N*dr + N*dr*2.0;
float1 c1=c*((float1)1.0 - Rs/sqrtl(dot(p1,p1)));
float1 c2=c*((float1)1.0 - Rs/sqrtl(dot(p2,p2)));
p1=p1 + (T*c1)*dtime2;
p2=p2 + (T*c2)*dtime2;
N=p2-p1;
N=N/sqrtl(dot(N,N));
T.x= -N.y; T.y=N.x; T.z=0.0;
speed=speed + T*c;
}
float3 screen=position*scale;
pixel(500+(int)(screen.x),300+(int)(screen.y),0xff0000);
screen.x=(float1)(j/100);
screen.y=sqrtl(dot(speed,speed))/400000.0;
pixel((int)(screen.x),900-(int)(screen.y),0xaa0000);
}
}
-
 #1207
#1207
A következő kérdés úgy hangzik, hogy lassulhat-e a fény a gravitáló tömeg fele közeledve? Mert ahhoz, hogy a gravitációt valamiféle fénytörésnek lehessen nevezni, le kellene lassulnia a fénynek erős gravitációs térben.
A fénysebesség konstans, azaz állandó mint a speciális, mind az általános relativitás elméletében(és a valós mérésekben is)
De ez az állandóság a gravitáció elméletében (az általános relativitásban) már csak lokális, a megfigyelő környezetében érvényes, hiszen nem tudunk felvenni globális koordinátarendszert.
http://www.relativitybook.com/resources/c_speedoflight.html
Ez azt is jelenti egyuttal, hogy globálisan szemlélődve NEM állandó a fény sebessége. Mivel nagyobb gravitációs térben lelassulnak az órák, ebból már sejthető, hogy a fény sebessége is kisebb ott.
Hiszen lassabb órávan mérünk ugyanakkora sebességet. Ha 300000km-ert csak 2 másodperc alatt teszünk meg, akkor már csak 150000km/s el haladunk('valójában' egy távoli pontról szemlélődve). De ha nekünk ez a 2 másodperc az óránk szerint 1 mertt lelassult, akkor 'valójában' 300000km/s-et mértünk.
Tehát a fény lassul erősebb gravitációs térben, egy TÁVOLI MEGFIGYELŐ SZERINT.
Ez a lassulás belső méréssel kimutathatatlan, mivel az mindig c(300000km/s) értéket ad.
Eddig minden rendben, de hogy lehet az, hogy a zuhanó testek gyorsulnak, ha a fény lassul? -
Albertus #1206 Gondolom tudod azt, hogy csak annak van gerjesztési színképe ami létezik, és pont ott rezonál ahol a tömege meghatározza..
-
 #1205
#1205
Mintha ezeket is valamiféle gerjesztési sorozat elemei lennének. -
 #1204
#1204
Felrajzoltam 'néhány' mezon(sárga vonalak), barion(lila), és lepton (piros) tömegét.
Nem ismerős?
-
 #1203
#1203
Ezt biztos ismered, a hidrogén atom Balmer-sorozata. A különböző energiaszintek közt 'ugráló' elektron sugározza ki.
-
 #1202
#1202
no problem -
 #1201
#1201
köszi a linkeket, bocs, h így hallgatok, csak közbe sok a dolgom :/
igyekszem mindet elolvasni, amivel fáradoztál!... -
 #1200
#1200
#1190
Én még messze vagyok a Higgs-től, először a kvarkokat kellene rendesen megérteni.
Lehet, hogy a Higgs az isten-részecske, avagy az isteni atom, ahogy Lederman írta. Ekkor minden részecske ennek a rezonanciája. Persze a dolog nem ilyen egyszerű amennyire egyszerűen hangzik.
Az is lehet, hogy a kvarkokat és a leptonokat egy még kisebb egység alkotja. Az egyik ilyen modell a preon modell.
http://www.google.hu/search?hl=hu&q=preon&btnG=Google+keres%C3%A9s&meta=
-
 #1199
#1199
Mégjobb
http://www.google.hu/search?hl=hu&q=particle+collision+simulation+photon&btnG=Keres%C3%A9s&meta= -
 #1198
#1198
Válogass..
http://www.google.hu/search?hl=hu&q=particle+collision+simulation&btnG=Google+keres%C3%A9s&meta=
-
 #1197
#1197
http://www.termeszetvilaga.hu/szamok/tv2005/tv0503/karolyhazi.html
Jaj beleolvastam... Jó jó , de nem matek.
Én maradok az arxiv.org-nál. Ott olyat is lehet olvasni, amit a tankönyvekben nem vagy még nem. -
pet0330 #1196 ÖÖ valami számitógépesre gondoltam :)
-
 #1195
#1195
Itt sok jó cikket találsz,
http://www.termeszetvilaga.hu/szamok/