Hunter
Az LHC Atlas detektora megkezdte a versengést
Gyors sikert könyvelhetett el a Nagy Hadronütköztető Atlas detektora. Néhány nappal a rekordnak számító 7 teraelektronvoltos fizikai program elindítása után máris az elméletek szerint a Higgs-bozonra utaló W-bozon részecskéket észleltek.
Ez önmagában nem olyan nagy szó, mivel a W bozonokat már más ütköztetőkben is észlelték, 1983-ban a CERN fedezte fel. Azonban mielőtt az LHC bármelyik detektora megkísérelne egy új részecskét felfedezni, újra fel kell fedeznie a már elfogadottakat. Fabiola Gianotti az Atlas csapat vezetője szerint nagyszerű jel, hogy ilyen hamar észlelték a részecskét. "Ez azt demonstrálja, hogy mind az LHC gyorsító, mind az Atlas kiválóan működik" - tette hozzá.
A gyenge kölcsönhatásáról (angolul weak) elnevezett W-bozon szinte azonnal leptonokká és neutrínókká bomlik. Az LHC múlt havi 7 TeV energiaszintre emelése óta a leptonokat - legyen egy pozitron vagy egy müon - két esetben észlelték az Atlas kaloriméterében és müonkamráiban. A neutrínó nem lép kölcsönhatásba a detektorral, jelenléte azonban kikövetkeztethető a bomlás teljes momentumának - hiányzó energiájának a kiegyensúlyozatlanságából.
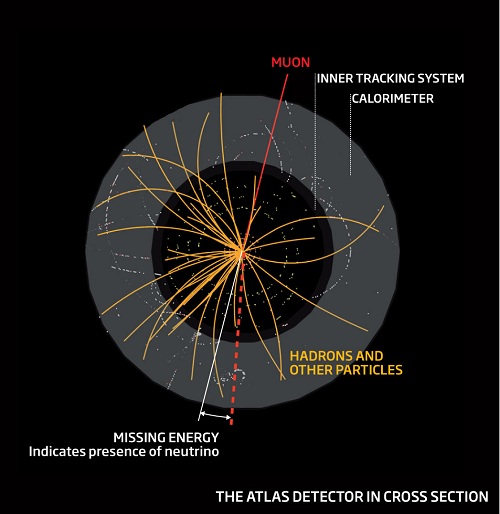
A hiányzó energia jelzi a neutrínók jelenlétét
"Az észlelés leginkább azért érdekes, mivel a standard modell szerint több új részecske, köztük a tömegért felelős Higgs-bozon is W-bozonokká bomlik. A W-bozonok nagyon lényegesek" - magyarázta Andreas Hoecker, az Atlas fizikusa.
A rivális CMS detektor együttműködés részéről David Barney fejezte ki elismerését, kiemelve, hogy az Atlas észlelése hozzájárul a két nagy általános célú detektor közötti egészséges versengéshez. Barney szerint számos érdekes eseményt kell még közösen felfedezniük, hogy teljes képet alkothassanak.
Ez önmagában nem olyan nagy szó, mivel a W bozonokat már más ütköztetőkben is észlelték, 1983-ban a CERN fedezte fel. Azonban mielőtt az LHC bármelyik detektora megkísérelne egy új részecskét felfedezni, újra fel kell fedeznie a már elfogadottakat. Fabiola Gianotti az Atlas csapat vezetője szerint nagyszerű jel, hogy ilyen hamar észlelték a részecskét. "Ez azt demonstrálja, hogy mind az LHC gyorsító, mind az Atlas kiválóan működik" - tette hozzá.
A gyenge kölcsönhatásáról (angolul weak) elnevezett W-bozon szinte azonnal leptonokká és neutrínókká bomlik. Az LHC múlt havi 7 TeV energiaszintre emelése óta a leptonokat - legyen egy pozitron vagy egy müon - két esetben észlelték az Atlas kaloriméterében és müonkamráiban. A neutrínó nem lép kölcsönhatásba a detektorral, jelenléte azonban kikövetkeztethető a bomlás teljes momentumának - hiányzó energiájának a kiegyensúlyozatlanságából.

A hiányzó energia jelzi a neutrínók jelenlétét
"Az észlelés leginkább azért érdekes, mivel a standard modell szerint több új részecske, köztük a tömegért felelős Higgs-bozon is W-bozonokká bomlik. A W-bozonok nagyon lényegesek" - magyarázta Andreas Hoecker, az Atlas fizikusa.
A rivális CMS detektor együttműködés részéről David Barney fejezte ki elismerését, kiemelve, hogy az Atlas észlelése hozzájárul a két nagy általános célú detektor közötti egészséges versengéshez. Barney szerint számos érdekes eseményt kell még közösen felfedezniük, hogy teljes képet alkothassanak.