Informatika és tudomány

Hunter

Elkészült a Mandelbrot "igazi" 3D-s változata

Többször megkíséreltek 3D-s Mandelbrot képet előállítani, de egyszer sem sikerült a valós fraktál viselkedés ábrázolása. A Mandelbulb viszont már szinte tökéletes.

Elkészült a legpontosabb háromdimenziós Mandelbrot fraktál, a Mandelbulb. A fraktálokat egy "ismétlődő" folyamat állítja elő, egy számon egy egyenletet alkalmaznak, majd a kapott eredményen újra és újra megismétlik ugyanezt az egyenletet. Amikor az eredményeket egy geometriai alakzattá alakítják olyan formákat kapnak, amik ugyanazokat a struktúrákat tartalmazzák más-más méreteken, vagyis önhasonlóvá válnak. A természetben bizonyos mértékig ilyen a levelek erezete, vagy a hópelyhek alakja. A dolog nehézsége az érdekes képek kialakítására alkalmas, megfelelő egyenletek megtalálásában rejlik.


Egy 2D-s fraktál, a régi demók egyik elengedhetetlen elemeként sokan találkozhattak vele

A leghíresebb fraktál egyenlet a kétdimenziós Mandelbrot-halmaz, amit a Yale Egyetem matematikusáról Benoit Mandelbrot, a "fraktál" név kitalálójáról neveztek el. Emellett természetesen számos más fraktál típus létezik két és három dimenzióban egyaránt, utóbbiakra talán a Menger-szivacs a legegyszerűbb példa.

Többször megkíséreltek 3D-s Mandelbrot képet előállítani, de egyszer sem sikerült a valós fraktál viselkedés ábrázolása, magyarázta Daniel White, egy amatőr brit fraktálkép készítő. Ha megforgatunk egy kétdimenziós Mandelbot fraktált, vagy egy magasabb dimenziójú matematikához fordulunk, könnyedén kaphatunk egy látszólag háromdimenziós Mandelbrotot, azonban egyik módszer sem adja vissza azt a részletességet és önhasonló alakzatokat, amit White szerint egy valódi 3D-s fraktálképnek tükröznie kellene. Ezért két évvel ezelőtt elhatározta, hogy megalkotja a Mandelbrot egy "valódi" 3D-s változatát.


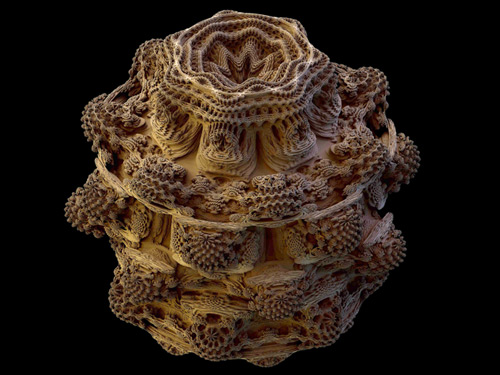
White Mandelbulbja

"Megpróbáltam megfigyelni hogyan működik az eredeti 2D-s Mandelbrot, hogy értelmezhessem három dimenzióban" - magyarázta. "Alkalmazhatunk összetett matematikákat, illetve nézhetjük a dolgokat geometriai szemszögből is." A komplex sík tulajdonságainak köszönhetően az utóbbi megközelítés működőképesnek tűnt.

A komplex sík épp olyan felület, mint a valós sík, csak ebben a koordináta-rendszerben a sík pontjait nem az (a,b) koordináták határozzák meg, hanem minden pontot egy a+bi alakú szám képvisel. Az "a" és "b" itt is a pont koordinátája, az "a" a szám valós része, a "b" a képzetes része. Az "i" szimbólum csak arra emlékeztet, hogy a számnak melyik része a képzetes. Az a+bi nagysága (abszolút értéke) egyenlő az a2+b2 négyzetgyökével. A számok szorzása a komplex síkon, megegyezik a forgatással, az összeadás pedig a síkon való eltolással.

A Mandelbrot sorozat előállításához csak ezeket a geometriai hatásokat kellett megismételni a sík minden egyes pontján. Egyesek a végtelenségig dagadtak, teljes egészében elhagyva a halmazt, míg mások nullára zsugorodtak. Egy tipikus fraktálkép különböző színei a nulla eléréséig lezajlott ismétlődések számát tükrözik.


A Mandelbulb közelről, ezerszeres nagyításnál is döbbenetes a részletessége

White kíváncsi volt, ha végrehajtja ugyanezeket a forgásokat és eltolásokat egy 3D-s térben, megkapja-e egy Mandelbrot-halmaz lényegét komplex számok alkalmazása nélkül. Ezek nem használhatók három dimenzióban, mivel csak két tengelyen helyezkednek el. 2007 novemberében közzétett egy képletet, ami már egészen közel járt a valódi 3D-s Mandelbrothoz, azonban még mindig nélkülözte a fraktál valós részletességét.

Ezután a fraktálok megszállottjai által látogatott Fractal Forums weboldal tagjaival közösen folytatta kutatását, aminek meg is lett az eredménye: Paul Nylander végül magasabb szintre emelte White képletét. Ezzel azonban White kutatása még nem ért véget, a bedfordi úriember szerint még a Mandelbulb sem tekinthető "valódi" 3D-s Mandelbrotnak. "Még mindig akadnak "homályos" részei, ahol nincs meg a kellő részletesség" - emelte ki. A probléma részben annak tudható be, hogy a Mandelbrot kiterjesztése a harmadik dimenzióra számos szubjektív választást igényel, ami nagyban befolyásolja a végeredményt. Például egy síkot úgy is kiterjeszthetünk 3D-be, hogy egy négyszöget kapjunk és úgy is, hogy egy gömb legyen az eredmény.


Mandelbulb "gerinc", mellette egy hasonló 2D-s Mandelbrot

"Ez egy érdekes elméleti feladat, minden attól függ, milyen tulajdonságokat akarunk megtartani a harmadik dimenzióban" - mondta Martin Turner a Manchester Egyetem fraktálokra szakosodott számítógép tudósa. A White által használt egyenletek alkalmasak lehetnek a feladat végrehajtására, azonban az algebra rendszere nem alkalmazható minden 3D-s matematikára. "A következő szakasz a matematikai szigor bevezetése lesz" - mondta Turner.

Hozzászólások

A témához csak regisztrált és bejelentkezett látogatók szólhatnak hozzá!
Bejelentkezéshez klikk ide
(Regisztráció a fórum nyitóoldalán)
  • ujfe #65
    Tisztelt Uraim és Hölgyeim !

    Megalázóan gyenge matematikai ismereteimre sikerült fényt derítenetek...már annyira, súlyos a helyzet, hogy a későbbi személyeskedést és néhány "hozzáértő" vitáját illetően is elvesztettem a fonalat... :)
    De le a kalappal, jó látni, hogy vannak körülöttünk olyanok akik ennyire értik a dolgukat ezen a területen és ha eljön a világ vége, nem lesz áram és számítógépek sem, elfogy a tüzelőanyag ami a gépeket hajtja, még mindig be tudnak majd üzemelni egy napórát, hogy ki tudják számolni mennyi időnk van még hátra...de mindezt csak azért, hogy mi, hozzá nem értő ateisták, reménykedhessünk, hogy tévednek :D
    De a viccet félre téve: őszintén becsülöm azokat akik ennyire vágják ezt a témát !
  • Epikurosz #64
    Apropó, ma belenéztem Bethlen Janiba az m1-en.
    Egy magyar matekos beszélt neki a Gömböcéről. Érdekes volt.
    Kara kánként folytatom tanításom.
  • Julius Caesar #63
    Ezt az idézeted nekünk a magyar tanárunk máshogy tanította, de lehet csak a fordítás volt más.

    Amúgy meg ezek a fraktálok lenyűgözőek. Imádom!
  • Epikurosz #62
    A Wikipédiáról vettem ennek a 3D-s Júlia-halmaznak a képét.
  • Epikurosz #61
    Kara kánként folytatom tanításom.
  • Epikurosz #60
    Az #56-os lényege az volt, hogy Donna Quijotina megint harcba indult. Ma velem, holnap veled, holnapután valaki mással.

    Egyébként, őszintén szólva engem csöppet sem zavar, jól elszórakozom rajta. Én úgy vagyok az emberekkel, hogy kiismerem őket, e célból néha ki is provokálom, hogy meddig lehet elmenni, aztán besorolom őket valahová, persze nem végleg, mert időnként előveszem a skatulyákat, és ellenőrzöm a régi címkék lejárati idejét.

    KillerBee, amellett - és ezt nem elfeledve! - hogy egy rendkívül intelligens és okos, sőt nekem éppenséggel szimpatikus nő, (a) erős bizonyítási kényszerben szenved, ami jórészt fiatal korának, illetve itteni újdonsült mivoltának tudható be, (b) szerintem van egy szkizoid vonása a személyiségének, ami konkrétan merevségben nyilvánul meg, de ez leküzdhető lenne, ha akarná.

    Először is meg kellene tanulnia pár dolgot - nem sokat, mert nagyjából egy kezemen meg tudom őket számolni:

    1. Különböző korú, felkészültségű, vallású, ideológiájú, mentalitású, ÉS kedvű emberek toppanak ide be. Ki gyakrabban, ki ritkábban. A kedvet azért hangsúlyozom, mert én elég gyakran poénkodni jövök be, mert például fáradt vagyok egy ledolgozott nap után, de azért benézek, mert egyrész megszokás, másrészt épp nincs jobb dolgom.

    2. Másrészt, vannak olyan ismeretek, amelyeket az ember nem szívesen osztana itt meg (mert azért tévedés ne essék, vannak, akik az internetről lopott ötletekből csinálnak pénzt maguknak!), és akkor az ember inkább viccesre veszi a figurát. Attól még nem hülye.

    3. Én is néha visszaolvasom évekkel ezelőtti hozzászólásaim, és magam is csodálkozom azon, hogy mennyi zöldség vagy reduncancia van bennük, hogy néha becsússzon valami értelmes is. De ezekért megéri elzagyválni a sok zöldséget. (Egyébként is erősen evolutív a gondolkodásom, de ez más téma.)

    4. Tele vagyok kérdésekkel és kétségekkel, amelyeket nem szívesen osztanék meg, mert úgy érzem, hogy túl mélyre mennék. Ilyenkor is jobb egy beszólás, egy poén, mert kitölti az űrt. Néha tévedek is. Mint ahogy összekevertem a nyomást a gravitációval, igaz, utólag megköszöntem a kiigazítást, de ezt valahogy az elvtársnő elfelejtette. Amúgy, nem csak nekem dörgöli az orrom alá múltbéli tévedéseim. Ugyanezt eljátszotta kvp-vel, babajagával, Doktor Kotásszal, bvalek2-vel és még másokkal is. Rögeszme. De ha ő ilyen, ám legyen, ezt is meg lehet szokni, sőt, el is lehet viselni, ha az ember kap valamit cserébe.
    De vajon a tényszerű, száraz ismeretek mindenért kárpótolnak? Én egyébként próbáltam már finoman figyelmeztetni KillerBee kartársat arra, hogy ne legyenek illúziói: ha nem 50 év múlva, akkor 100 év múlva biztosan megjelenik a mesterséges intelligencia. Tehát, pusztán a tudás bálványozása lehet, hogy jobb, mint a fizikai erőnek, vagy a pénznek az imádata, de nem ez az non plus ultra.
    Pál apostol mondja a Rómaiakhoz írt levelében a következőket:
    „Szólhatok az emberek vagy az angyalok nyelvén, ha szeretet nincs bennem, csak zengő érc vagyok vagy pengő cimbalom. Lehet prófétáló tehetségem, ismerhetem az összes titkokat és mind a tudományokat, hitemmel elmozdíthatom a hegyeket, ha szeretet nincs bennem, mit sem érek. Szétoszthatom mindenemet a nélkülözők közt, odaadhatom a testemet is égőáldozatul, ha szeretet nincs bennem, mit sem használ nekem. A szeretet türelmes, a szeretet jóságos, a szeretet nem féltékeny, nem kérkedik, nem is kevély. Nem tapintatlan, nem keresi a maga javát, nem gerjed haragra, a rosszat nem rója fel. Nem örül a gonoszságnak, örömét az igazság győzelmében leli. Mindent eltűr, mindent elhisz, mindent remél, mindent elvisel. S a szeretet nem szűnik meg soha. A prófétálás végetér, a nyelvek elhallgatnak, a tudomány elenyészik. Most megismerésünk csak töredékes, és töredékes a prófétálásunk is. Ha azonban elérkezik a tökéletes, ami töredékes, az véget ér. Gyermekkoromban úgy beszéltem, mint a gyerek, úgy gondolkoztam, mint a gyerek, úgy ítéltem, mint a gyerek. De amikor elértem a férfikort, elhagytam a gyerek szokásait. Ma még csak tükörben, homályosan látunk, akkor majd színről színre. Most még csak töredékes a tudásom, akkor majd úgy ismerek mindent, ahogy most engem ismernek. Addig megmarad a hit, a remény és a szeretet, ez a három, de közülük a legnagyobb a szeretet.”

    Ezt az idézet egyébként nem lehet elég sokszor elolvani. Engem, például most, ahogy ide beírtam, az döbbentett meg, hogy egy keresztény apostol a túlbuzgóságot, a vakhitet is kevesebbre tartja a szeretetnél. Világosan kimondja, hogy „hitemmel elmozdíthatom a hegyeket, ha szeretet nincs bennem, mit sem érek”. Sőt, a végén, még külön ki is hangsúlyozza: [i]„megmarad a hit, a remény és a szeretet, ez a három, de közülük a legnagyobb a szeretet.”[i]

    5. Ezt elfelejtettem, de lehet, hogy majd szembe jut. De annyira már nem is fontos.
  • physis #59
    Az alapkereteket nem értem, egy tartalmi részt viszont külön is fontosnak tartok, szerintem azt jó volt felhoznod.

    Először az alapkeretek:

    #43-ban egy személyesen hozzám írt szakmai kérdést egy magánjellegű, személyes hangú felvetés követett Epikuroszról:

    ,,(Mellékesen: meglepődtem, hogy Epikurosz egy éve még értelmes dolgokat is tudott írni.)''


    A felvetés hozzám íródott (kapcsolt komment), nem pedig kapcsolatlan hozzászólásként lett elküldve.

    Én egyszerűen egy (nick)név szerint hozzám intézett üzenetre válaszoltam. A válaszban több helyen is utaltam rá -- igaz, nem mindenütt elég alaposan -- hogy itt az én személyes SG-használatomról van szó: én a magam részéről ismeretelméleti kérdések esettanulmányaként (is) használom az SG-t.

    Ugyanazzal a civil hozzáállással reagáltam a magánjellegű felvetésre, mint magára a kérdésre. Mindkét estben ugyanaz volt a ,,célom'', ,,szándékom'': hogy válaszoljak olyasvalamire, amit személyesen hozzám szólva vetettek föl. Ugyanúgy, ahogy arra is válaszolok, ha az utcán valaki megkérdezi az időt.

    Más lenne a helyzet, ha a hírek topikjaiba bértopikoltam volna kéretlenül és zavaróan. Szintén más lenne a helyzet ha mások vitáiba szóltam volna bele tiszteletlenül, az egyéni érzelmeket, hátteret és kontextust figyelembe nem vevő módon.

    Ez az összemosás nem korrekt, a személyes sértés részt vissautasítom.

    Epikurosz kommentjei ,,a Vonal alatt'', a hírektől elválasztva jelennek meg. Profilján megadta személyes blogját, és egyik hozzászólásában egy wikipédia-kontribúcióját is. Ezenkívül általában a kontextusból is adódik, hogy nem kelti hamisan a hitelesség látszatát. Általában nem támad alapból (inkább a régi viták és sérelmek lángolnak fel újra meg újra). Nem kapott még büntetőpontot.

    Mindezért, nem látom, hogy etikai megítélés alá esnék.

    Bár az #56-os üzenetedet nem tudom megragadni, de az üzenet felhoz egy nagyon lényeges és tartalmas témát, ezt nagyon fontosnak tartom, erre külön is szeretnék válaszolni. Annyira különböző területeket érint, mint a tudomány népszerűsítése, a tévhitek elleni harc, a családon belüli erőszak kezelése.

    Nem mellébeszélésképp említettem az ismeretelméletet, hanem nagyon is gyakorlati okból. Ha az ember a gyakorikerdesek.hu-n a ,,család'' és az ,,önismeret'' rovatban az odaíró kamaszok kérdéseire válaszol

    * miért iszik apu állandóan
    * normális dolog-e a mindennapi verés
    * miért vannak vízióim),
    ....

    akkor hamar beleütközik a válaszoló abba a korlátba, hogy nem elég csak valami szaktudományos választ odaönteni a kamaszok elé, hanem igenis érzékelni kell azt, hogy ők csak azokat a problémákat tudják maguknak megoldani, amit saját a maguk gondolkodásmódjával is át tudnak látni. És ismerni kell ezt is.

    Igenis figyelembe kell venni, hogy a kamaszok nem formális logikával gondolkodnak, hanem analógiák mentén, és a gondolkodásmódjuk alapvetően esszencialista, vagyis nem szerződések és struktúrák révén látják szerveződni a világot, hanem sok dolgot valahogy úgy elve adottnak tekintenek, valahogy úgy, mint az arisztotelészi fizika (a vas azért süllyed el, mert ,,nehéz'', a fa azért úszik, mert ,,könnyű''). A gyakorikerdesek.hu-n az ismeretelmélet nem mellébeszélés, hanem mindennapos, húsbavágó, véres gyakorlat: aki azt nem veszi figyelembe, az nem fog tud segíteni a kamaszoknak, aki pedig igen, az sikeresen segít. Nekem is van egy csomó elrontott próbálkozásom. E terepen a türelmetlenség szinte biztos kudarchoz vezet.

    Mindez persze csak lazán illik az Általad felvetett kérdésekhez, de mégis előhoztam, mert talán ez is hozzájárult ahhoz, hogy nem értem az Epikurosz iránti erősen negatív érzelmi-etikai töltést, nem tudok mit kezdeni ezzel, teljesen idegen a számomra.

    Az SG a ,,Vonal fölé'' teszi a cikkeket, ott jön szóba a hitelesség kérdése. A ,,Vonal alatt'' vannak a hozzászólások, ott nem a szakmai hitelesség a lényeg, hanem a kibeszélés és a feldolgozás. Itt szó szerint mindenre van példa: analógiás gondolkodás, esszencializmus, arisztotelészi fizika, antropomorfizmus, moralizálás. És épp az a jó, hogy ezek ott vannak, mert épp az a jó, hogy előjönnek. Ha a tudományt csak az iskolában öntik le az emberek előtt, és sehol sem beszélgethetnek róla az emberek a saját maguk nyelvén, a saját maguk felvetései szerint, akkor szerintem éppen hogy megnehezedik a tudomány népszerűsítése, nem pedig megkönnyebbedik. Az analógiás és az esszencialista hozzáállás valamiféle nem kiirtandó szégyen, hanem inkább kibeszélendő dolog. Csacska dolog lenne rejtegetni, szégyellni. Egyrészt szőnyeg alá nyomva attól még ottmarad, másrészt valaha a tudomány részei voltak ezek a gondolati keretek is, és az abból nőtt ki lassan.
  • Epikurosz #58
    (az Rákóczi induló dallamára köll énekelni, zengeni, masírozva)
    Kara kánként folytatom tanításom.
  • Epikurosz #57
    Fel, fel csatára, a határra,
    gaz ellenségnek birtokára,
    öljük az ellent, szúrjuk, vágjuk,
    csípjük, rúgjuk, lórúl lerántjuk.
    Sej!
  • KillerBee #56
    "Epikurosz egyszerűen csak túláltalánosított egy általában korrekt modellt, de ez belefér az SG-n általában is folyó viták hangulatába, és a tudománytörténetnek is része a modellek állandó kalibrálása"

    A tudománytörténet figyelembe vételével sem helyes ezt a marhaságot egy "általában korrekt modell" túláltalánosításának nevezni, hiszen az adott problémát (gravitációs erő egy gömbhéjon ill. egy homogén gömbön belül) ugyanaz a Newton válaszolta meg több mint 300 ével ezelőtt, aki magát a gravitációs törvényt és a pontmodellt megalkotta. Sőt Newton ugyanazzal a módszerrel (integrálás) és ugyanazon lépésben jutott a pontszerű testek modelljéhez, mint amellyel megalkotta a gömb(héj) gravitációs modelljét (shell theorem). A kettő keverését még extrém eufemizmussal sem lehet túláltalánosításnak nevezni, sokkal inkább a newtoni gravitációs elmélet alapvető meg nem értésének.

    "A gravitációs példában is igaza volt alapvetően"

    Alapvetően mennyire lehet igaza annak, aki alapvetően nem érti az elméletet, és a megfigyelésekkel és az elmélettel homlokegyenest ellenkező dolgot állít?

    Amint akkor szerinted nyilván abban is alapvetően igaza van, hogy a termodinamikában a víznek három kritikus pontja van: az olvadáspont, a forráspont és 374 Celsius fok (nyomás megjelölése nélkül!). Hiszen ő csak "túláltalánosította" a kritikus pont fogalmát - idézem: "kritikus pont = kritikus hőmérséklet, amikor egy anyag halmazállapotot vált"- vagyis kiterjesztette, ahogy akkor írta, mikor szembesítették a tényekkel.

    "A kommenteket nemcsak azért szoktam olvasni, hogy szaktudományos kérdésekben tájékozódjam, hanem azért is, hogy a történelem tudománytörténeti zege-zugait kicsiben újra-elismételve újra lássam, és ismeretelméleti kérdések is felmerüljenek."

    Igen sajnálatos, hogy ebbe neked belefér az is, hogy "alapvetően" igazat adva neki erkölcsi támogatást nyújts olyan embernek, aki többszáz éve megcáfolt tévhiteket terjesztve a fizikai topicokat sorra telesza/órja mindenféle képtelenségekkel. Számomra elképzelhetetlen mértékű, a jellemtelenséggel határos arcátlanság és cinizmus (vagy pusztán szervilizmus? - mindegy) szükségeltetik ehhez. Nem értem, milyen szándék vezetett, mindenesetre számomra hiteltelen emberré váltál. (Tudom, túléled.)
    Válasz 'physis' üzenetére (#46)
    http://magyarorszag21.blog.hu/2009/04/16/p1069869
    \"Terrorists may attack the open society, but only governments can abolish it.\" (The Pirate Party)
További bejegyzések a fórumban...