Gyurkity Péter
Olcsóbb alternatíva a Mars megközelítésére

Egy matematikus javaslata szerint jóval kevesebb üzemanyaggal is elérhetnénk szomszédunkat.
A Mars az utóbbi időben (mint az emberiség soron következő célpontja az űrkutatásban, illetve az égi szomszédokra indított küldetések terén) kiemelt szerepet kap a szaksajtóban. Szó esett itt már ember nélküli, illetve űrhajósok részvételével tervezett expedíciókról, bár a konkrét lépésekre csak az évtized végén, illetve a 2020-as években kerül majd sor. Most egy nem igazán új alternatíva kínál olcsóbb megoldást a problémára.
A matematikusként dolgozó Edward Belbruno nemrég közzétett dokumentumában a Föld és a Mars közötti utazások költségeinek lefaragásáról, az ezek során elhasznált üzemanyag mennyiségének jelentős csökkentéséről olvashatunk. Ezt egy viszonylag egyszerű lépéssel érné el a szakember, az eddig gyakran használt Hohmann transzfer pálya helyett ugyanis a Hold esetében már többször bevált ballisztikus befogás (ballistic capture) módszerével oldaná meg a szomszédhoz történő utazást, ami ugyan jóval több időt venne igénybe, ám lecsökkentené az eszközök által hordozott üzemanyag mennyiségét és ezzel olcsóbb küldetéseket tenne lehetővé.
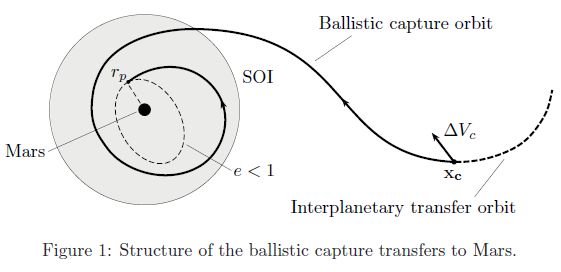
A megoldás lényege a szomszédos égitestek megközelítésének módszerében rejlik. A Hohman transzfer pálya esetében az erre kijelölt eszközt egy szűkebb orbitális pályán gyorsítják fel, majd ez elliptikus szakasz révén egy tágabb pályára állítják, amelyen végül a felé közeledő égitesthez érve le kell fékeznie, hogy a kiszemelt égitest körül keringjen tovább. A fékezési manőver jelentős mennyiségű üzemanyagot igényel, ezt már a fellövéskor biztosítani kell, ami természetesen növeli az eszköz súlyát és a költségeket. A ballisztikus befogás alkalmazása révén viszont ugyanezen eszközt korábban útnak indítanák, a megfelelő pályára állítanák, mégpedig az égitesthez képest némileg alacsonyabb sebességen, lehetővé téve, hogy az (jelen esetben a Mars) utolérje az űrben száguldó eszközt és orbitális pályára „szippantsa”, állítsa azt.
Az előzetes számítások szerint a második módszerhez 25 százalékkal kevesebb üzemanyag is elegendő lenne, ezzel komoly pénzeket takaríthatnának meg mindazon projektek, amelyek a Mars elérését tűzték ki célul. Az anyagot az elkövetkező hónapokban a területtel foglalkozó kollégák véleményezik majd, itt pedig több problémára, így például a többi bolygó gravitációs hatásának kérdésére is megnyugtató választ kell adni. A Hold esetében ez a kilencvenes évek elején már sikerült, akkor éppen Belbruno segítségével tudták pályán tartani és kísérőnkre letenni a japán Hiten holdszondát, az eljárást pedig azóta több alkalommal is sikerrel alkalmazták.
A Mars az utóbbi időben (mint az emberiség soron következő célpontja az űrkutatásban, illetve az égi szomszédokra indított küldetések terén) kiemelt szerepet kap a szaksajtóban. Szó esett itt már ember nélküli, illetve űrhajósok részvételével tervezett expedíciókról, bár a konkrét lépésekre csak az évtized végén, illetve a 2020-as években kerül majd sor. Most egy nem igazán új alternatíva kínál olcsóbb megoldást a problémára.
A matematikusként dolgozó Edward Belbruno nemrég közzétett dokumentumában a Föld és a Mars közötti utazások költségeinek lefaragásáról, az ezek során elhasznált üzemanyag mennyiségének jelentős csökkentéséről olvashatunk. Ezt egy viszonylag egyszerű lépéssel érné el a szakember, az eddig gyakran használt Hohmann transzfer pálya helyett ugyanis a Hold esetében már többször bevált ballisztikus befogás (ballistic capture) módszerével oldaná meg a szomszédhoz történő utazást, ami ugyan jóval több időt venne igénybe, ám lecsökkentené az eszközök által hordozott üzemanyag mennyiségét és ezzel olcsóbb küldetéseket tenne lehetővé.

A megoldás lényege a szomszédos égitestek megközelítésének módszerében rejlik. A Hohman transzfer pálya esetében az erre kijelölt eszközt egy szűkebb orbitális pályán gyorsítják fel, majd ez elliptikus szakasz révén egy tágabb pályára állítják, amelyen végül a felé közeledő égitesthez érve le kell fékeznie, hogy a kiszemelt égitest körül keringjen tovább. A fékezési manőver jelentős mennyiségű üzemanyagot igényel, ezt már a fellövéskor biztosítani kell, ami természetesen növeli az eszköz súlyát és a költségeket. A ballisztikus befogás alkalmazása révén viszont ugyanezen eszközt korábban útnak indítanák, a megfelelő pályára állítanák, mégpedig az égitesthez képest némileg alacsonyabb sebességen, lehetővé téve, hogy az (jelen esetben a Mars) utolérje az űrben száguldó eszközt és orbitális pályára „szippantsa”, állítsa azt.
Az előzetes számítások szerint a második módszerhez 25 százalékkal kevesebb üzemanyag is elegendő lenne, ezzel komoly pénzeket takaríthatnának meg mindazon projektek, amelyek a Mars elérését tűzték ki célul. Az anyagot az elkövetkező hónapokban a területtel foglalkozó kollégák véleményezik majd, itt pedig több problémára, így például a többi bolygó gravitációs hatásának kérdésére is megnyugtató választ kell adni. A Hold esetében ez a kilencvenes évek elején már sikerült, akkor éppen Belbruno segítségével tudták pályán tartani és kísérőnkre letenni a japán Hiten holdszondát, az eljárást pedig azóta több alkalommal is sikerrel alkalmazták.