Hunter
A minósziak megelőzték Arkhimédeszt?
Minószi falfestményeken több, mint ezer évvel korábban megjelentek azok a geometriai alakzatok, melyeket a köztudatban Arkhimédesznek tulajdonítunk.
A festmények matematikai jegyei azt sugallják, hogy a késő bronzkori Minósz i.e. 1650 környékén sokkal előbbre járt a geometria ismeretében, mint azt eddig bárki feltételezte volna, állapította meg az Athéni Nemzeti Műszaki Egyetem kutató csoportja. A festményekre a jelenlegi Santorini, akkor Théra szigetén, az egykori minószi város, Akrotiri egyik épületének ásatása és restaurálása közben bukkantak rá. A városra egy vulkán kitörés mért végzetes csapást i.e. 1650 körül, viszont a vastag hamuréteg számos épületet és műtárgyat konzervált.
 Eddig 10 épületet tártak fel, köztük egy szokatlanul nagy alapterületűt, ami az ősi rakpart közelében állt egykoron. Méretéből és terjedelmes falfestményeiből ítélve a Xeste 3 névre keresztelt építmény valamilyen középület lehetett, például egy templom, vagy valamilyen rituális ünnepségeknek otthont adó csarnok.
Eddig 10 épületet tártak fel, köztük egy szokatlanul nagy alapterületűt, ami az ősi rakpart közelében állt egykoron. Méretéből és terjedelmes falfestményeiből ítélve a Xeste 3 névre keresztelt építmény valamilyen középület lehetett, például egy templom, vagy valamilyen rituális ünnepségeknek otthont adó csarnok.
A festmények legszembetűnőbb jegyeit spirálok egy sorozata adja, melyek mindegyike megközelítőleg 32 centiméter átmérőjű és pöttyökkel díszített. A kutató csapat vezetője, Constantin Papaodysseus, számítógép tudós bebizonyította, hogy ezek az alakzatok szinte tökéletes arkhimédeszi spirálok.
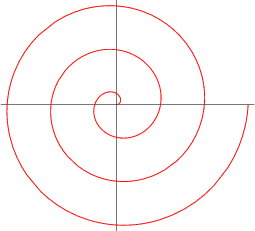
Sok spirális alakzat fordul elő a természetben is, gondoljunk csak a csigaházra, Arkhimédesz spirálja azonban egyikre sem hasonlít. Két egymást követő íve közötti távolság állandó, azaz egy állandó szélességű csigavonalról van szó, ami a kutatók szerint nem létezik a természetben. Papaodysseus szerint ez a legkorábbi fejlett geometriai alakzat, amivel eddig találkoztak, a következő ismert alakzat nem kevesebb, mint 1300 évvel később bukkant fel.
 Mivel azokból az időkből nincsenek ismert írásos emlékek, ezért a kutatók nem tudják, mennyire lehetett tudatos a geometria alkalmazása a minószi művészek munkájában. Elvileg a legrosszabb esetben is legalább kísérletezniük kellett a geometriai eszközökkel ahhoz, hogy megalkossák ezeket a festményeket. A spirálokat már évekkel ezelőtt észlelték a területen dolgozó régészek, azonban eddig mindenki úgy vélte, hogy azok szabad kézzel készültek. Papaodysseus elemzései azonban azt bizonyítják, hogy az ívek túl pontosak ehhez, általában legfeljebb egyharmad milliméterrel térnek el az egyszerű, ám annál szigorúbb matematikai formulától.
Mivel azokból az időkből nincsenek ismert írásos emlékek, ezért a kutatók nem tudják, mennyire lehetett tudatos a geometria alkalmazása a minószi művészek munkájában. Elvileg a legrosszabb esetben is legalább kísérletezniük kellett a geometriai eszközökkel ahhoz, hogy megalkossák ezeket a festményeket. A spirálokat már évekkel ezelőtt észlelték a területen dolgozó régészek, azonban eddig mindenki úgy vélte, hogy azok szabad kézzel készültek. Papaodysseus elemzései azonban azt bizonyítják, hogy az ívek túl pontosak ehhez, általában legfeljebb egyharmad milliméterrel térnek el az egyszerű, ám annál szigorúbb matematikai formulától.
Papodysseus szerint sablonokkal érhették el ezt a pontosságot, melyek az elemzések szerint a könnyebb szállíthatóság és a festmények felvitele érdekében hat részre voltak darabolva, a kérdés csupán az, hogyan készültek maguk a sablonok.
A festmények matematikai jegyei azt sugallják, hogy a késő bronzkori Minósz i.e. 1650 környékén sokkal előbbre járt a geometria ismeretében, mint azt eddig bárki feltételezte volna, állapította meg az Athéni Nemzeti Műszaki Egyetem kutató csoportja. A festményekre a jelenlegi Santorini, akkor Théra szigetén, az egykori minószi város, Akrotiri egyik épületének ásatása és restaurálása közben bukkantak rá. A városra egy vulkán kitörés mért végzetes csapást i.e. 1650 körül, viszont a vastag hamuréteg számos épületet és műtárgyat konzervált.
 Eddig 10 épületet tártak fel, köztük egy szokatlanul nagy alapterületűt, ami az ősi rakpart közelében állt egykoron. Méretéből és terjedelmes falfestményeiből ítélve a Xeste 3 névre keresztelt építmény valamilyen középület lehetett, például egy templom, vagy valamilyen rituális ünnepségeknek otthont adó csarnok.
Eddig 10 épületet tártak fel, köztük egy szokatlanul nagy alapterületűt, ami az ősi rakpart közelében állt egykoron. Méretéből és terjedelmes falfestményeiből ítélve a Xeste 3 névre keresztelt építmény valamilyen középület lehetett, például egy templom, vagy valamilyen rituális ünnepségeknek otthont adó csarnok. A festmények legszembetűnőbb jegyeit spirálok egy sorozata adja, melyek mindegyike megközelítőleg 32 centiméter átmérőjű és pöttyökkel díszített. A kutató csapat vezetője, Constantin Papaodysseus, számítógép tudós bebizonyította, hogy ezek az alakzatok szinte tökéletes arkhimédeszi spirálok.
Sok spirális alakzat fordul elő a természetben is, gondoljunk csak a csigaházra, Arkhimédesz spirálja azonban egyikre sem hasonlít. Két egymást követő íve közötti távolság állandó, azaz egy állandó szélességű csigavonalról van szó, ami a kutatók szerint nem létezik a természetben. Papaodysseus szerint ez a legkorábbi fejlett geometriai alakzat, amivel eddig találkoztak, a következő ismert alakzat nem kevesebb, mint 1300 évvel később bukkant fel.
 Mivel azokból az időkből nincsenek ismert írásos emlékek, ezért a kutatók nem tudják, mennyire lehetett tudatos a geometria alkalmazása a minószi művészek munkájában. Elvileg a legrosszabb esetben is legalább kísérletezniük kellett a geometriai eszközökkel ahhoz, hogy megalkossák ezeket a festményeket. A spirálokat már évekkel ezelőtt észlelték a területen dolgozó régészek, azonban eddig mindenki úgy vélte, hogy azok szabad kézzel készültek. Papaodysseus elemzései azonban azt bizonyítják, hogy az ívek túl pontosak ehhez, általában legfeljebb egyharmad milliméterrel térnek el az egyszerű, ám annál szigorúbb matematikai formulától.
Mivel azokból az időkből nincsenek ismert írásos emlékek, ezért a kutatók nem tudják, mennyire lehetett tudatos a geometria alkalmazása a minószi művészek munkájában. Elvileg a legrosszabb esetben is legalább kísérletezniük kellett a geometriai eszközökkel ahhoz, hogy megalkossák ezeket a festményeket. A spirálokat már évekkel ezelőtt észlelték a területen dolgozó régészek, azonban eddig mindenki úgy vélte, hogy azok szabad kézzel készültek. Papaodysseus elemzései azonban azt bizonyítják, hogy az ívek túl pontosak ehhez, általában legfeljebb egyharmad milliméterrel térnek el az egyszerű, ám annál szigorúbb matematikai formulától.Papodysseus szerint sablonokkal érhették el ezt a pontosságot, melyek az elemzések szerint a könnyebb szállíthatóság és a festmények felvitele érdekében hat részre voltak darabolva, a kérdés csupán az, hogyan készültek maguk a sablonok.

