729
Elméleti fizika - Elektrodinamika, Elméleti mechanika, Kvantumfizika
-
Irasidus #569 Ugyanígy nem lehetséges, itt kint sem, ha a szökéssi sebesseg kisebb. Ez ugyanaza fizika, ugyanazt írja le. Egyébként keringhet a polúsok felett. Bocs de hülye vagy még mindig. -
hiper fizikus #568 Szia !
"diagrammokkal egyszerűen illusztrálható a téridő oksági struktúrája"
De ez az oksági struktúra egészen más az eseményhizonton belül mint kívül .
"de ettől még az eseményhorizontot átlépve nem fogsz tapasztalni más fizikai törvényeket vagy ilyesmit."
A fizikai törvények valóban nem lehetnek mások, de másképen viselkednek .
Pl. a fekete lyuk belsejében egy ottani bolygó körül nem keringhet egy ottani hold, mert a köztük lévő saját kisebb gravitációs terük csak egyirányú(!) lehet, tehát ezért ott nincs rendes kerigési pályájuk sem, ami elengedhetetlen a hold meglétéhez .

Utoljára szerkesztette: hiper fizikus, 2018.11.22. 14:01:26 -
 #567
#567
az általad idézett bekezdés arról szól, hogy a penrose diagrammokkal egyszerűen illusztrálható a téridő oksági struktúrája, és hogy ez hogy van ábrázolva a diagrammokon. de a téridő fizikája nem változik meg az eseményhorizontot átlépve, sempedig nem lesz végtelen. az csak a szingularitásnál történik meg.
azért jelölik egyirányúnak a teret az eseményhorizonton belül, mert az eseményhorizontot átépve végül úgyis a szingularitásba jutunk, más megoldás nem lehetséges. de ettől még az eseményhorizontot átlépve nem fogsz tapasztalni más fizikai törvényeket vagy ilyesmit. egészen a szingularitás eléréséig. a szingularitás meg csak egy pont a fekete luk közepén.
Utoljára szerkesztette: botyika, 2018.11.22. 13:51:34 -
Irasidus #566 Google fordító? Lol. :D -
 #565
#565
meg nyilván nem is igaz, mert nincs a környéken olyan tömegű fekete lyuk aminek beleférnénk az eseményhorizontjába. de egyébként mi is egy eseményhorizonton belül élünk, a megfigyelhető univerzum eseményhorizontján belül. -
hiper fizikus #564 A WP eng Penrose diagram cikkben azt írják, hogy
"This is due to the interchanging of timelike and spacelike coordinates within the horizon of a black hole (since space is uni-directional within the horizon, just as time is uni-directional outside the horizon). "
Ezt úgy fordítja a Google fordító, hogy
"Ez annak köszönhető, hogy a fekete lyuk horizontján a timelike és spacelike koordinátákat váltják (mivel a tér egyirányú a horizonton belül, ahogy az idő egyirányú a horizonton kívül)."
Tehát az "egyirányú teret" nem az újamból szoptam ki . Természetesen ebbe az egyirányú térbe belefér az is, hogy csak 90 fokos szögig bezárólag lehet eltérni tőle .

-
fonak #563 Van olyan elképzelés, hogy mi is egy fekete lyuk eseményhorizontján belül élünk, bár ez nyilván nem a többség által elfogadott gondolat. -
 #562
#562
illetve egyébként pont úgy kell elképzelni mint az ábrán. az eseményhorizont egy gömbfelület (álló külső szemlélők ugyanakkorának látják), a szingularitás meg egy végtelen sűrűségű pont a fekete luk közepén. szóval a kettő teljesen különbözik. a végtelenek a szingularitásnál vannak. -
 #561
#561
1. -esre a válaszom az, hogy szerintem nem végtelen az eseményhorizontnál semmi. egy 10ezer naptömegű fekete lyuk eseményhorizontját gond nélkül át lehet lépni és életben maradni egy embernek. sőt, gondolj bele egy hatalmas nagy tömegű fekete lyuk közelében is simán élhetnénk az eseményhorizonton belül egy bolygón, ami elég messze van a szingularitástól. csak elhagyni nem tudnánk sosem a téridőnek ezt a tartományát, mert ahhoz végtelen gyorsulásra lenne szükség. (legalábbis szerintem)
2. -esre a válasz szerintem az, hogy te mint külső megfigyelő nem tudsz mondani semmit az eseményhorizonton belül történő dolgokról, ez így igaz.
3.- sztem lehet más alakja, pl ha két fekete lyuk köröz egymás körül, akkor nem hiszem hogy gömb az eseményhorizontjuk.
-
Irasidus #560 "{;egyirányú tér}"
A térben való mozgásnak van értelme, ennek az általad kitalált szónak nincs. Az, hogy a részecske vagy a fény a fekete lyuk tömegközpontja felé halad, nem azt jelenti, hogy a tér egyirányú, máskülönben nem csak egyenesen úton haladhat, hanem oldal irányba is, 90 fokos szögig bezárólag. Megint egy újabb bizonyítéka annak, hogy halandzsázol, és fogalmad sincs miről beszélsz. Nézd még mindig látszik, hogy kilóg a lóláb, és olyan sötét vagy mint az éjszaka.
Utoljára szerkesztette: Irasidus, 2018.11.22. 06:18:10 -
hiper fizikus #559 ..ia !
A Minkowski diagramot a speciális relativitáselmélet, a Penrose diagramot az általános relativitáselmélet használja . Köszönöm, hogy felhívtad rá a figyelmemet, de a "stílusod" kíváni valókat hagy maga után . A Penrose diagram olyan Minkowski diagram, ami a végtelent rendszeres véges ábrázolásra képezi le. Ezt a WP eng Penrose diagram cikkéből bogarásztam ki némi személyes interpletációval . Számomra meglepő újdonság az, hogy nem csak timelike{;egyiányú idő} hanem spacelike{;egyirányú tér} koodinátarendszert is bevezet a geometriájába . Olvashatod a cikkben, hogy az eseményhorizont osztja szét a timelike és a spacelike tereket, mint ha a téridőnek két fázisa lenne . Tehát a megszokot geometriánknak az eseményhorizontnál vége szakad, az "egyirányú tér" geometria pedig csak absztrakció, valami más világ . Vagyis a timelike{;egyiányú idő} geometria görbülete a meredekségével egyetemben az eseményhorizontnál véget ér, és valami más spacelike{;egyirányú tér} alakulás követi . Evvel nem azt akarom bizonygatni, hogy neked nincs igazad, hanem azt, hogy amikor arra utalok, hogy a fekete lyuk belsejének a fizikája a mi fizikánkhoz képest más valami, akkor igazam van, mert ugye az "egyirányú tér" fizika más, mint a miénk, persze ott sem lehet kauzális összeviszaság .

-
Irasidus #558 Kérlek vezesd már le, mire gondolsz, ha már fizikáról beszélünk ne szád járjon, hanem a fizikatudásod. Szóval? Amúgy szerinted ha " téridő görbülete az eseményhorizontnál végtelen" akkor a felénél még végtelenebb lesz? Tiszta önellentmondás.
Amúgy a valóság ezzel szemben ez, a kulcsszó a mit keresnél (ha lenne egy csöpp eszed, de nincs), az a Minkowski diagram, vagy Penrose diagram. Mindkét esetben láthatod a nem végtelent.
Utoljára szerkesztette: Irasidus, 2018.11.21. 22:15:16 -
 #557
#557
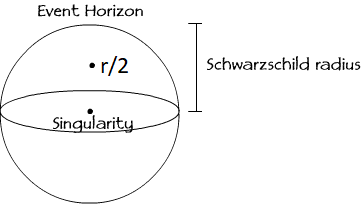
A Schwarzschild sugár fele az bent van a feketelyuk-ban.
Most akkor mire gondoltál tényleg, a gömb felületére, vagy a sugár felére?
-
Irasidus #556 Hát persze, hogy nem te kevered össze, miért is ismernél be valamit ami nyilvánvalóan ordító hülyeség, és csak hárman mondjuk, hogy összekevered? Á dehogy... Miért is lenne bőr az arcodon, hogy beismerd. Túl nagy kérés ez egy embertől. Tényleg.
#477
"A fotonokat valóban elnyeli az eseményhorizont, de éppen hogy azt nem tudjuk, érsd hogy nincs rá egyenletünk, hogy milyen útvonalon haladnak az eseményhorizontot ferdén megcélzó fénysugarak az eseményhorizont mögött, mert ott már nincs téridő, csak egy lyuk és nagyon nagyon fekete !"
#550
"A téridő görbülete az eseményhorizontnál végtelen lesz . Tehát az eseményhorizontnál végtelen lesz a gravitációs gyorsulás ."
Utoljára szerkesztette: Irasidus, 2018.11.21. 21:54:40 -
hiper fizikus #555 Vagy hogy jobban értsed: ad meg számszerűen az Schwarzschild sugár felénél a téridő görbületének a meredekségét ! - nem tudod . -
hiper fizikus #554 Nem szia !
Egyáltalán nem keverem össze az eseményhorizontot és a szingularitást: az eseményhorizon labda felület közepén van a szingularitás pont .
Mindenki olvashatja nálad, hogy nem én kezdtem újra a személyeskedést, ill. a durvulást !
A gravitációs lencse elképzelésemet meg egy kicsit újra értelmeztem, amit Te nem szoktál .
Azt javaslom, hogy térjünk vissza a fizikára, mondjuk ad meg az esményhorizontnál lévő gravitációs gyorsulás képletét; hogy fére ne érdzs nem a szingularitásnál lévőt, de ne a Newton fizikával számold hanem a relativitásossal .

Utoljára szerkesztette: hiper fizikus, 2018.11.21. 20:41:48 -
Irasidus #553 Bizony, hogy nem kellet volna hülyeséget beszélned, és igaza van botyika, és én is írtam #479 már. Egyre kínosabb amit művelsz. Az eseményhorizont az határ amelyen túl az események nem befolyásolhatják a külső megfigyelőt. Te ezt összekevered a szingularitással. Annyit se tudsz, mint egy discoveryn nevelődött, félművelt ütődött ember. Fogalmad sem volt, hogy mi az Einstein-gyűrű amit már tíz évesek fújnak, akiket érdekel a csillagászat. Szánalmas a vergődésed. És ez bullshitartist amit most előadsz, eszemet baromság megint. Neked nincs semmiféle szégyenérzeted, nincs lelkiismereted? Csak nyomatod tovább, és megjátszod az okosat. Tiszta nem egyszerűen egy buta balfék vagy, hanem egy szánalomra méltó buta balfék...
Utoljára szerkesztette: Irasidus, 2018.11.21. 19:01:50 -
hiper fizikus #552 Szia !
1) Nem azt kellett volna mondanom, hogy az eseményhorizntnál végtelen a téridő görbülete, hanem azt, hogy végtelen a téridő görbületének a meredeksége . Márpedig ez a meredekség adja a gravitációs gyorsulást, vagy ha nem, akkor mond meg, hogy mi !?
2) Az úgy van, hogy az eseményhorizont vonatkoztatásában is két inerciarendszer egy-egy megfigyelővel adott .
Az egyik átlépi a szingulárist a saját ideje szerin, a másik megállni látszik a saját ideje szerint . Mindkét tényállítás igaz, és csak azért igaz, mert a relativitáselmélet ilyesmin furcsaságokat szolgáltat a hétköznapokhoz szokot emberek részére .
Tehát ha Te azt mondod, hogy átmegy rajta és ha Én azt mondom hogy nem megy át rajta, akkor mindketőnknek igaza van, csak más szempontból . Azt viszont Te sem tudod megmondani érdzs kiszámolni, hogy az eseményhorizontól a szingularitásig menyi időbe telik neki az út, sőt azt sem, hogy milyen lesz az út pályája . Én szempontom viszont megtudja mondani: semmilyen sem lesz se az idője se a pályája .
3) A fekete lyukak méretét az általános relativitáselmélet nemkorlátozza se lefele se felfele . Azon is vitatkoznak, hogy az eseményhorizontnak egyáltalán lehet-e más alakja, mint a gömb .

-
 #551
#551
az eseményhorizontnál nem lesz végtelen a gravitációs gyorsulás, se a téridő görbülete. az a szingularitásnál van. az eseményhorizontot átlépve nem érez az ember semmi különöset. vannak fekete lyukak amiknek az eseményhorizontja sokkal nagyobb mint a naprendszerünk. -
hiper fizikus #550 Szia !
Ha mindenképpen ki akarod húzni belőlem:
A gravitációs gyorsulás a téridő görbületétől függ . A téridő görbülete az eseményhorizontnál végtelen lesz . Tehát az eseményhorizontnál végtelen lesz a gravitációs gyorsulás . A fekete lyuk belsejében nem lehet konkrétan számolni az általános relativitáselmélet képleteivel . Tehát a fekete lyuk belseje egy ismeretlen tartomány, vagyis határozatlan .

-
kl24h #549 " Elméletileg mekkora a gravitáció a fekete lyuk belsejében, tehát végtelen nagy vagy csak nagyon nagy?"
Konkrétan a fekete lyuk belsejében ahol maximális a gravitáció, az végtelen nagy vagy csak nagyon nagy? -
hiper fizikus #548 Szia
"görbéhez húzott érintő (a Földön) fogja mutatni a csillag látszólagos pozícióját"
Igen, ez így is van, de attól, hogy eltér a szöge, attól még a látszólagos távolsága is kimérhető .

"gravitáció a fekete lyuk belsejében"
Ez fogas kérdés . Ezen még gondolkodnom kell .

-
hiper fizikus #547 Szia !
Persze, hogy értem ! Egyszer azt írod, hogy nem adtak neki nevet, aztán meg azt írod, hogy mások ne is adjanak neki nevet !
Ez hülyeség !
-
 #546
#546

Szerintem félreértettél, sőt biztos.
Általános eset, hogy amikor valaki valamilyen jelenséget elsőkénet felfedez, akkor ő adhat neki nevet, mint felfedező.
Erről ebben az esetben már lekéstünk, mert ugye ezek nem új jelenségek, ahogy te is linkeltél be képeket, tehát már régebben felfedezték őket.
Amire én gondoltam, hogy ha majd te is találsz a galaxisban egy ilyen jelenséget, és szépen levezeted, hogy melyik égitest hatására hogy hajlott meg a fény, milyen mértékben, milyen messze innen, stb-stb, akkor akár meg is lehet próbálni bejegyeztetni a neveket, amiket az #540 -ben kitaláltál. Tehát hivatalossá tenni, hogy ezentúl így hívják őket majd a szakirodalomban. Érted?
Utoljára szerkesztette: Steel, 2018.11.20. 21:01:55 -
kl24h #545 Azért írtam, hogy "nem helyes", mert nem az lesz az eltérés, amennyivel hosszabb a görbe, hanem a görbéhez húzott érintő (a Földön) fogja mutatni a csillag látszólagos pozícióját, ami más eredményhez vezet.
Egy másik érdekes téma: Elméletileg mekkora a gravitáció a fekete lyuk belsejében, tehát végtelen nagy vagy csak nagyon nagy?
Utoljára szerkesztette: kl24h, 2018.11.20. 21:03:40 -
hiper fizikus #544 Szia ! Ez a hozzászólásod korrekt, de amit én magyaráztam annak is van értelme, nem ütközik a kettő !
Utoljára szerkesztette: hiper fizikus, 2018.11.20. 20:50:03 -
hiper fizikus #543 Szia !
Ezek szerint a montászom neked nem elég, legyen hát:
Áttörés a csillagászatban: 56 új gravitációs lencsét fedezett fel a mesterséges intelligencia
Ez a link igazán ide való:
az első és az ötödik képe példa az Einstein-gyűrűre
a harmadik képe példa az Einstein-félholdra
a második és a negyedik képe példa az Einstein-(vegyes)szegmensekre
Ez szintén egy példa az Eistein-(nem vegyes)káprázatra .
Ez példa az Einstein-csillámlásra . -
kl24h #542 A parallaxis szög mérésekor legjobban el tudja görbíteni a fényt a Föld gravitációja, ami azt jelenti, hogy nem ugyanaz a szöget mérnénk az Északi póluson mint a Déli póluson (feltételezve hogy minkét póluson lehet látni a mérendő csillagot). A fényt csak akkor nem görbíti el a Föld, ha pontosan egy olyan szélességi körben végezzük és abban az órában, amikor a "távcsövünket" pont függőlegesre kellene állítani, mert ekkor nem lesz fényelhajlás a Föld részéről. Ezenkívül sokkal kisebb hatása van a Napnak, mivel egy félévre végezzük el a mérést a Nap ellentétes elgörbítést végez. A mérendő csillag gravitációja a parallaxis szög mérésekor nincs hatással.
Még egy fontos dolog, ha távolabbi csillagot szeretnénk mérni csak ezzel a módszerrel és tegyük fel hogy lehetséges is, ekkor figyelembe kell venni a Nap sebességét, pontosabban a keringését ami kb. 220 km/s, ez is már valami egy félév alatt.
Tehát végeredményben a gravitációnak nagyon kis hatása van ezért eléggé pontosan lehet mérni.
Ha más mérési módszereket alkalmazunk, akkor annak megfelelően kell figyelembe venni a gravitációt és más hatásokat.
"Ugye téged nem csak a közeli átlagos csillagok távolságának mérése érdekel a metagalaxis csillagászata korában ?" A kérdést általánosan tettem fel, tehát közeli vagy távoli csillagok esetére.
Utoljára szerkesztette: kl24h, 2018.11.20. 20:45:40 -
 #541
#541
Kreatív magyar neveket találtál. :)
Ha egyszer majd felfedezel egy nevezetes élő példát rájuk, még akár hivatalosan is bejegyezhetik. -
hiper fizikus #540 Szia !
Értem ; tehát ha az Einstein-gyűrű nem teljes, akkor mi nevezzük szegmentális elhajlásnak vagy Einstein-szegmenseknek ; és ennek a szegmentizálódásnak legyen két megnevezett szélsői változata, mégpedig az Einstein-félhold és az Einstein-káprázat . Természetesen az Einsten-félhold a kiterjedtebb szegmentális elhajlás, és az Einstein-káprázat alig kiterjedt szegmentális elhajlások társasága ; az Einstein-káprázat egyik eleme pedig legyen az Einstein-csillámlás .
Hogy tetszik ?
Utoljára szerkesztette: hiper fizikus, 2018.11.20. 14:43:51 -
 #539
#539
Amikor az Einstein gyűrű helyett csak foltok, vagy akár egy folt jelenik meg, akkor azt a legtöbb írásban részleges, vagy szegmentált elhajlásnak nevezik. Nincs hivatalos neve.
A maximális elhajlás-kor jön létre az Einstein gyűrű, a minimális elhajláskor pedig szinte csak egy kis apró folt, vagy pont, amire az #530 -ban nagy valószínűséggel te is gondoltál. -
hiper fizikus #538 Akkor minek nevezik azt, amikor a gravitációslencse efektus következtében csak két ellentétes folt jelenik meg, mint ahogyan a montázsomon is láthatod, és nem Einstein-gyűrű ? Mert ugye nevezni kell valahogyan !

-
 #537
#537
Nem. A gravitációs lencse az maga az effektus neve. Ott van az oldalon, 74-szer fordul elő. (Tehát nem. Itt nem én vagyok vak.)
A teljes gyűrű-t pedig valójában Einstein gyűrű-nek nevezik.
Fényelhajlás pedig minden esetben van, amikor gravitációs lencse effektusról van szó, értelemszerűen.
"A csillagból kiinduló összes fénysugárra hat a nagytömegű objektum..."
Hát ez?
Még azokra a fotonokra is, melyek homlokegyeneset az ellenkező irányba lépnek ki, azaz eleve a nagytömegű objektummal ellenkező irányba terjednek?
"A gyakorlatról meg annyit, hogy ez a topik elméleti fizika, tehát nem a gyakorlatról szól, hanem az elméletről..."
És ami már eleve az elméletben megbukik, esélye sincs, hogy a gyakorlatban működjön. -
hiper fizikus #536 Szia !
Ha nem vagy vak, akkor ezen a montázson láthatod a gravitációs lencsét és a fényelhajlást együtt . Gravitációs lencse akkor van ha teljes gyűrű keletkezik, és fényelhajlás pedig akkor van, ha csak kis folt keletkezik, igaz ami igaz két darab kis folt, ha ezek kicsik akkor pontnak nyilváníthatjuk őket, ill. van középpontjuk . A csillagból kiinduló összes fénysugárra hat a nagytömegű objektum, nem csak a fénykúpra, csak hogy ebből fénykúpnyit látunk, ami fénysugarak kévéje, ha ez kicsi, akkor fénysugárnak nyilváníthatjuk . A módszerem csak anyiban változik, hogy nem az egyik hanem mindkét foltra kell-lehet alkalmazni . A gyakorlatról meg annyit, hogy ez a topik elméleti fizika, tehát nem a gyakorlatról szól, hanem az elméletről, ha a gyakorlattal akarsz foglalkozni, akkor tessék menj egy másik topikba . Ha tudnánk paralaxist mérni a galaxisok között, akkor ott a két folt pozíciója is változna egy kicsit a paralaxis következtében .

Utoljára szerkesztette: hiper fizikus, 2018.11.20. 11:06:02 -
 #535
#535
Szerintem megint fordítva ülsz a lovon.
Pontosan a gravitációs lencse annak a jelenségnek a következménye, amit te már az #527 óta ragozol.
"egyáltalán nem a gravitációs lencse hatásról van szó, hanem csak a gravitáció okozta pontszerű fényforrás fénysugarának az elgörbüléséről"
Az ugye világos, hogy egy csillag fénye minden irányba terjed. A csillag és a megfigyelő között elhelyezkedő nagy gravitációjú test minden irányba ható gravitációs mezője egy kúpvetületnyi fényforrást elgörbít.
A te "módszerednek" pont semmi hasznak nincs a gyakorlatban, mióta tudjuk, hogy nincs abszolút fix pont az univerzumban. Ennek a háromszögednek is állandóan változni fognak a szárai, mert mozog a csillag, a naprendszer, és a Föld is.
A paralaxis szög mérésével olyan objektumok mérhetőek ki, melyek fényforrását nem görbítik el más égitestek, vagy erős gravitációs mezők.
Utoljára szerkesztette: Steel, 2018.11.20. 08:38:55 -
hiper fizikus #534 Szia !
"nem tartalmaz semmilyen fizikai információt, márpedig a szög meghatározásához a tömeg nagyságát ismerni kell"
A tömeg nagyságát ismerhetjük más mérésekből kifolyólag . Ha több tömegről van szó, akkor mindegyiket számbavesszük .

Utoljára szerkesztette: hiper fizikus, 2018.11.19. 21:58:35 -
hiper fizikus #533 Sziasztok !
kl24h látja jól, azt amit magyaráztam ! Irasidus, egyáltalán nem a gravitációs lencse hatásról van szó, hanem csak a gravitáció okozta pontszerű fényforrás fénysugarának az elgörbüléséről ! Mivel különösebben nem sértegettél, ezért nem vágok vissza, nincs miért !
kl24h, paralaxis szög mérésével csak a közeli csillagok mérhetők ki, a galaxisok pedig végkép nem mérhetők ki . De ha egy olyan paralaxis szög mérésével mérhető közeli csilagot akarunk megmérni, amit egy ritka véletlenül egybeeső nagy tömeg elgörbít, akkor az ő fénysugara is görbe lesz a paralaxis szög mérés mindkét végponti mérésénél . No jó ez csak elméleti eset, mert a gyakorlatban nem igen van ilyenre példa .
"Görbült oldallal számolni egy kicsit bonyolultabb és kell ismerni pontosan a görbültségét."
Ez így igaz, de én elvonatkoztattam egy kicsit - ugye tudod mi az az elvonatkoztatás - hogy érzékletesebb legyen a megoldás. Persze ha akarod, akkor bíbelődhetsz a görbe kiintegrálásávál, de ekkor is a görbe hossza a (AC+CB) -től még hosszabb lesz, mint az AB szakasz hossza . Görbültség ismerete a releváns tömegektől függ, kedvező esetben egy tömegtől . Írtam is, hogy "amit bonyolultan számítani lehet" . Ugye téged nem csak a közeli átlagos csillagok távolságának mérése érdekel a metagalaxis csillagászata korában ?

-
kl24h #532 Az hogy a fény görbe utat tesz meg, az út csak egy kevéssel hosszabb az egyeneshez képest, mivel nagyon kicsi az elhajlás.
A paralaxis szög mérésével meg lehet határozni a csillag távolságát, csak az a helyzet, hogy ez a számítás a hasonló háromszögekkel végzett számítással történik és a háromszögek oldalai egyenesek. A mi esetünkben nem mindegyik oldal egyenes, ezért másképp kell számolni. Nem az lesz a különbség, amit leírtál, hogy mennyivel hosszabb a görbült oldal, hanem sokkal nagyobb. Görbült oldallal számolni egy kicsit bonyolultabb és kell ismerni pontosan a görbültségét.
Más távolságmérési módszerrel a fény elhajlása nem okoz gondot. Másképpen is nagyon kevés az elhajlás, tehát eléggé pontosan lehet így is (paralaxis szög mérésével) meghatározni a távolságot.
Utoljára szerkesztette: kl24h, 2018.11.19. 20:13:08 -
Irasidus #531 Ha jól értem, te most a gravitációs lencse hatásról beszélsz. Ennek geometriája kicsi összetettebb, és a probléma a te Móriczka elképzeléseddel az, hogy nem tartalmaz semmilyen fizikai információt, márpedig a szög meghatározásához a tömeg nagyságát ismerni kell, mert az határozza meg a törés nagyságát, mivel a valóságban nincs viszonyítási pont, azaz nincs "egyes" távolság, csak a lencsét látod. És még kismillió dolgot nem vettél figyelembe, mivel itt egy lencsehatásról van szó.
Gravitational lensing formalism
Utoljára szerkesztette: Irasidus, 2018.11.19. 20:03:46 -
hiper fizikus #530 Szia !
A görbülség hozza létre a háromszög két szárát . Evvel a két szárral lesz hosszabb a látszólagos távolság . Mondjuk a távolságmérés legyen a fény spektrumeltolódásával és a fényerővel mérve . Mi nem helyes ebben ? Talán így érthetőbb lesz: A háromszög legyen A, B és C pontú . Az A pont a Föd, B pont a kimérendű égitest helye, és a C pont a fénysugár legnagyobb görbületének a pontja . Különbözet = AB - (AC + CB) ; arány = AB/(AC + CB) . Amit egyszerűen mérni lehet az a (AC + CB) spektroszkópiai távolság, és amit bonyolultan számítani lehet az az AC és az CB közti szög .

Utoljára szerkesztette: hiper fizikus, 2018.11.18. 21:51:17