89
-
Irasidus #89 Miért kellene minden pontján végtelennek lennie? -
nnyiti #88 "Ha végtelen sok csillag lenne, akkor végtelen sok anyag, és így végtelen sok energia."
Végtelen nagy térben...
attól h egy rendszerben végtelen energia van, nem biztos h minden pontjában végtelen energia van, ha a redszer végtelen
de ez a topik már úgyis meghalt, csak így visszatévedtem :D -
 #87
#87
Ígérem, hogy este el fogom olvasni ezeket a hsz-eket, mert hangzásra olyan jóknak tűnnek. -
philcsy #86 "Vagyis ez az ami a pusztán "matematikai modellt" megkülönbözteti a Fizikai valóságot leíró modellektől."
Egy szóval sem mondtam hogy a matematikai modellek mind fizikai modellek.
Én azt mondtam hogy a fizikai modellek matematikai modellek.
1. Kérlek definiáld mit értesz fizikában bizonyíték alatt.
2. "Mindig a kijelentőnek kell bizonyítani." Igen. A kijelentés viszont az hogy a standard gyertyák abszolúlt fényességét ismerjük. Te jössz.
3. "Az illető objektum ismert abszolút (hogy 10 parsec = 32,6 fényév távolságból milyen fényes lenne" Ez a 2.-hoz tartozik. Honnan ismered az abszolult fényességüket?
4. "Elnézés az nnyit volt, aki szerint a fény "elvész"." Mi köze a fény elveszésének a világegyetem időbeni homogenitásához?
5. "Az írtad feltételezi, gondoltam tudod mely csillagászok feltételezik, ha már azt írtad feltételezik..." Az áltlad pontosnak tartott wikipédiára gondoltam. -
Irasidus #85 Sorry a kép nem sikerült, az Androméda galaxist ábrázolta volna, javaslom mindenkinek nézze meg inkább a saját szemével mit lát. Csillagot benne biztos nem... -
Irasidus #84
Az Androméda galaxisban egyetlen csillagot sem látsz, mert ilyen távolságból egyetlen csillag sem látható(!), a Galaxist magát mégis látod, és ez "csak" pár 100 milliárd csillag, nem végtelen! Végtelen sok csillagról meg el sem tudom képzelni, hogy látható lenne. Most jönne az, hogy ennél távolabbi objektumot akkor miért nem látunk? Ezt igyekeztem elmondani: mert 1. Nem statikus "Olbersi" világegyetemben élünk, a fény vöröseltolódáson megy át - de meg van nem vész el (nnytinek). 2. Illetve nem végtelen sok van belőle, hanem "végtelenül" kevés ahhoz, hogy lássuk...
(és így folytatódik a mondat) ... a matematikai modell egyrészt nem definiált (absztrakt, szimbolikus)matematikai objektumokból (például számokból, vektorokból) áll, másrészt az objektumok közötti relációkból. A matematikai modell a matematika szimbólumrendszerén keresztül teremt kapcsolatot a vizsgált rendszer be- és kimenő jellemzői között.
...
A homológ és analóg modellalkotás legtöbbször nem közvetlenül, hanem a matematikai modellen keresztül történik. Ezek az úgynevezett másodlagos leképezések. Jellemzőjük, hogy a jelenség lényegét tükröző absztrahált modellhez először a matematikai modellt alkotjuk meg.
Ezután — felhasználva a hasonlóságelmélet azon törvényszerűségét, hogy a hasonló jelenségeket leíró matematikai összefüggések formálisan azonosak vagy azonos alakra transzformálhatók — létrehozzuk a matematikai modellnek megfelelő, az eredeti jelenséggel homológ vagy analóg modellt. (és figyelj itt jön a lényeg) Az ily módon másodlagos jellegű, a leíró matematikai formulát leképező analóg modell már semmilyen szemléletes kapcsolatban nem áll az eredeti jelenséggel, csak a be- és kimenő jellemzők közti kapcsolatot adja vissza.
Természetesen számítási szempontból minden modell matematikai, de a modellnek a valós fizikai tapasztalatokkal való összevetését a modell tesztelésének (validálásának esetleg verifikálásának) nevezzük. Vagyis ez az ami a pusztán "matematikai modellt" megkülönbözteti a Fizikai valóságot leíró modellektől...
Hipotézis: tudományos feltételezés amely tartalmazza a bizonyítás, vagy cáfolás kritériumait. A nagyon pontosan, tehát gyakran a matematika nyelvén megfogalmazott hipotéziseket tudományos modellnek nevezzük, több egymással összekapcsolható tesztelt modell egzakt tudományos elméletet (teóriát) alkot.
1. A matematikába létezik a bizonyítás, a fizikában bizonyíték.
2. Mindig a kijelentőnek kell bizonyítani. (Honnan tudjam mit állítasz? A mérést ha cáfolni tudod akkor gondolom ismered is őket, nem tudom, hogy mit mondhatnék még róluk ezek után. Szóval te jössz.)
3. Az illető objektum ismert abszolút (hogy 10 parsec = 32,6 fényév távolságból milyen fényes lenne), és mért látszó fényességének összevetésével, felhasználva azt, hogy a fényesség a távolság négyzetével fordított arányban csökken, kiszámítható annak távolsága, ami jó közelítéssel megegyezik az őt tartalmazó galaxis távolságával. A standard gyertya módszerek (pl. cefeida periódus-fényesség reláció, gömbhalmazok, planetáris ködök fényessége) pontos távolságértéket adnak, de "csak" néhány százmillió fényév távolságon belül alkalmazhatóak. Kivételt képeznek a szupernóvák, amelyek segítségével több milliárd fényévre lévő galaxisok távolsága is megbecsülhető.
3. Mint fentebb kifejtettem ez nem matematikai modell.
4. Elnézés az nnyit volt, aki szerint a fény "elvész".
5. Az írtad feltételezi, gondoltam tudod mely csillagászok feltételezik, ha már azt írtad feltételezik... -
djhambi #83 Gondoltam, hogy beokoskodok a témába, talán építőjellegűt is tudnék hozzátenni.
Érdemes elgondolkodni azon, hogy egy pontszerű tényforrás körül zárt felületen ugyanannyi energia halad át. (Poynting-vektor)
Érdemes elgondolkodni azon, hogy az emberi szem egy bizonyos apró felületen lát csak. Így az ember távolodva a fényforrástól egyre kisebbet lát, amíg a fényforrástól embernyi távolságon lévő gömbön a fény energiája ugyanakkora, mint bármilyen sugárra.
Nem tudom, célszerű-e a biológiát a fizikába mosni, ha a fizikában sincs egyetértés.
Ha végtelen sok csillag lenne, akkor végtelen sok anyag, és így végtelen sok energia.
Érdemes hallgatni philcsy-re, mert sokkal többször igaza van, mint nekem.
-
nnyiti #82 Hát nem tudom veled megértetni magam, nem értem én magyarázom ennyire rosszul? Senki más nem érti amit kérdezek?
Vegyük akkor kicsit lassabban:
-van egy pici leded. Kint vagyunk az űrben, nincs semmilyen zavaró közted és a led között. A led tőled 6millió kilóméterre van. Látod a ledet? Nem. Az intenzitása ugyan annyi, mégsem látod a nagy távolság miatt. Eddig remélem egyetértünk.
Most bonyolítunk:
-2 led van. Ugyanolyan erősek. Mérjük a fény "láthatóságát" (ezt neveztem eddig fényességnek) annak mértékében, mennyire szűkül össze a pupillád a fény hatására. Ha egy led 1 méterre van a szemedtől, az legyen 1 egység. Abból a tapasztalatból kiindulva, h a távolabb lévő fény kevésbé érzékelhető, egy két méterre lévő lednek kisebb lesz a láthatósága 1 egységnél. tegyük fel legyen 0,98, ha megengedsz nekem egy becslést. Tehát két led, ha egymás mellett van egy méterre a szemedtől akkor 2 egység a láthatósága, de ha az egyik led hátrébb van 1 méterrel, akkor a szemedbe érkező fény érzékelhetősége csak 1,98. Na ez a következő check point. Ha ezzel is egyetértünk akkor továbbmehetünk.
Vegyük be a paradoxont:
-Ez ha jól értelmeztem, azt állítja a paradoxon, h azért nem létezhet végtelen csillag mert az egymás mögött lévő csillagok fénye annyira felerősítené egymást, h tiszta fényesség lenne minden. Check?
-Most lássuk be h vannak a szemnek érzékelési korlátai, legyen ez a példában lévő led, ha egy kilométer távolságba van a szemtől, akkor már nem érzékelhető. Egységben mondva 0 hatással van a szemre, nincs hatással a pupillára, nem érkezik inger az agyba stb. Nem azt mondom h nincs fény, csak azt h nem látom. Na ha ezt megértetted és elfogattad akkor mehetünk tovább.
-Az állítás szerint (ha jól értem) ha végtelen led van egyás mögött, akkor tiszta fényesség kellene legyen.
-Végezzünk elméletben egy mérést. Tegyük fel h elvégeztük a mérést minden egyes méteren h külön külön mennyire van hatással a pupillára a fényforrás, és azt kaptuk h : 1méteren nyilván 1 egység 2m=0,98 3m=0,95 4m=0,91 ... 1000m=0 Remélem nem nehéz elképzelni, h elméletben végeztünk egy mérést.
Most jön a lényeg:
-fogunk ledeket, és egymás mögé helyezzük méterenként. Előzőleg tisztáztuk h ha egy led 1m-re van 1 egységnyire hat ránk, ha 2m-re van 0,98-nyira, és ha egymás mögött vannak 1 és 2 méterre akkor ezeket a számokat össze kell adjuk, és annyira lesz hatással a szemünkre, tehát 1,98 egységnyire. Namost nem 2őt, hanem 1000 db ledet helyezünk egymás mögé, és az elvégzett kisérletekben a számokat összeadjuk (1+,098+0,95+0,91...) kijön egy szám, legyen mondjuk 453,65. Ez azt jelenti, h 1000 db led ha méterenként egymás mögött van, olyan hatással van a pupillára, mintha az első ledet helyettesítenénk egy 453,65-ször erősebb leddel. Ez így elvileg eddig stimmelnie kéne.
És most jön az apropó! Ha 1001 ledet teszek egymás mögé méterenként, akkor az 1001-edig led érzékelhetősége már nem adódik hozzá, a pupillánk nem fog változni attól h beraktuk az 1001-ediket, mert már olyan messze van h egyedül lenne akkor se látszana! Ugyanígy az 1002-edik, 1003-adik ésígy végtelenségig...
Hiába létezik külömbség a fényerősség intenzitásában, ha 1000 vagy 1001 ledet rakunk egymás mögé, a szem ezt már nem fogja érezni. Az 1000 és az 1233242134 db led között se fog tudni fényintenzitásban különbséget érzékelni a pupilla.
Fuh... ezt már komolyan halál részletesen leírtam, ha ebből nem érted, feladom... -
philcsy #81 a.)
"Ezek szerint nem árulod el mit értesz modell alatt csak használod a szót. A hipotézis nem modell."
Furcsa hogy pont te kéred rajtam számon a definíciókat. Keress rá a google-ben ha nem tudod mit jelent.
A matematikai modell: valamilyen vizsgált rendszerben lejátszódó jelenségnek, a vizsgálat szempontjából lényeges tulajdonságai közötti összefüggések matematikai megfogalmazása.
A hipotézis mindaddig "bölcsleti onanizálás" amíg nem fogalmazod meg a matematika nyelvén.
b.)
"Ezt illenék alátámasztani is."
Álljon már meg a menet. Nem azt kell alátámasztani hogy 'A standard gyertyák miért nem állandók?', hanem azt hogy 'A standard gyertyák miért állandók?'
c.)
"Egyébként távolságot nem csak így lehet mérni. A Hubble-törvény. [...] Itt amint látod szó sincs standard gyertyákról."
Olvass már utána a Hubble-törvénynek mielőtt hivatkozol rá. Hubble-törvény a standard gyertyák fényességének ismeretére támaszkodik támaszkodik.
Szereted a wiki, nem? Ez onnan van:
"The parameters that appear in Hubble’s law: velocities and distances, are not directly measured. In reality we determine, say, a supernova brightness, which provides information about its distance [...]"
Kiegészítés: Nem csak 1a típusú szupernóvát használnak standard gyertyaként.
Az egész kozmológia a standard gyertyák fényességének ismeretén alapszik.
És honnan ismernénk a a standard gyertyák fényességét?
Matematikai modellekből!
Az 1a típusú szupernóvák keletkezését ismertnek vesszük, feltételezzük hogy az ott folyó folyamatokat ismerjük.
Ezek után a megfelelő matematikai modellel:
Definiáljuk a Chandrasekhar-határt, felhasználva a kvantuum-mechanika Pauli-féle kizárási elvét.
Chandrasekhar-határ: Annak a csillagnak a tömege amelyben a gravitációból származó nyomás, egyenlő a Pauli-féle kizárási elvből adódó degenerációs nyomással.
Tegyük fel hogy az 1a tipusú szupernóvaként ismert objektumok olyan stabil fehértörpékből keletkeztek melyek annyi anyagot nyeltek el hogy a tömegük átlépte a Chandrasekhar-határt.
Ekkor össze kell roppanniuk, mivel a degenerációs nyomás az összehúzódással nem nő. Az összehúzódás miadt hirtelen beinduló magfúziót észleljük 1a típusú szupernóvaként.
Ebben a matematikai modellben két feltételezést használtunk:
-Az egyik úgy kezdődik hogy 'Tegyük fel ...'
-A másik az hogy a kvantuum-mechanika érvényességi határa kiterjed a fehértörpékre is. Ez nem egyértelmű, mivel a kvantuum-mechanikát eddig csak viszonylag kis méretekben teszteltük. Pont ez a fizika egyik sötét foltja.
Egy szupernóva robbanásnál vannak kvantuum-os hatások is, de a nagy tömeg miadt fellépnek relativisztikus hatások is.
Folytassam hogy ezzel milyen ingoványos talajra ért a dolog vagy elég? Hány olyan megbízható elméletet tudsz amely ilyen körülmények között biztonságosan használható? (értsd: ilyen körülmények között kísérletben ellenőrizték)
Persze vannak más standard gyertyák is. Például a cefeidák pulzálásának frekvenciájából meghatározható a maximális abszolult fényességük.
És hogy határozható meg, tippelj.
Matematikai modellel. Egy fúziós reakcióban fellépő oszcilláció matematikai modellezésével.
d.)
"Ok, kicsoda?"
Az általad idézett wikipédia oldal!
"Azt is hozzá kell tennünk az előbbiekhez, hogyha figyelembe vesszük a fény véges sebességét, hogy:
3. a csillagoknak nem csak térben, hanem időben is „egyenletesen” kell eloszlaniuk,
hiszen mennél távolabbra nézünk, annál régebbi, amit nézünk. Ez végtelen skálán azt jelenti, hogy
3*. a Világegyetemnek végtelen öregnek kell lennie, mindenféle drámaibb változások nélkül a csillagok természetében."
Ez a világegyetem időbeni homogenitását jelenti.
e.)
"Ezzel nem tudom mit szerettél volna mondani, "
Szerintem érthető voltam...
"rendere elfelejted az energiamegmaradás törvényét"
Hol? Idézd és magyarázd is meg hogy miért. Ne csak úgy mond.
Mi a hiba a következő mondatban:
"Az ABSZOLÚLT fényesség független a távolságtól, a LÁTSZÓLAGOS fényesség nem."
Elemezzük:
'Az ABSZOLÚLT fényesség független a távolságtól.' Igaz? Igen.
'A LÁTSZÓLAGOS fényesség nem független a távolságtól.' Igaz? Igen.
Megint egy kis matek, a diszkrétebbik fajtából: (Igaz 'és operátor' Igaz) = Igaz
f.)
"Már elkezdtem írni, egy kis türelem, válaszolok erre is - csak ez hosszabb lesz."
Várom... -
jamborl #80 a vegtelen ter, vegtelen csillagot(anyagot) feltetelez, persze lehet filozofalni rajta, hogy miert nem
szerintem ez a 4 felteves lehetseges:
ter veges - ido veges (errol gondolom nem kell sokat irni)
ter veges - ido vegtelen (minden fenyes lenne es mar megsultunk volna)
ter vegtelen - ido vegtelen (ha vegtelen ideje szorjak a vegtelen szamu csillagok a fenyuket (egy vegtelen terben), akkor a vegtelen csillag vegtelen energiaja eljutott volna hozzank es minden csillag energiaja eljutott volna a ter osszes pontjara, igy hozzank is, ha betartjuk az energia megmaradas torvenyet. mivel a hidrogen alakul at egyre nehezebb anyagokka a csillagokban, es elobb utobb kialszik, kihul, ezert veszit az energiajabol. ha vegtelen szamu csillag lenne vegtelen ideje, akkor mar mind kihult volna. ez is a veges idot bizonyitja. mint az is hogy az univerzum tagul, es hogy egyes csillagok fenye meg nem ert el hozzank.)
ter vegtelen - ido veges (ido veges vagyis volt egy kezdete, de akkor mi volt az anyaggal? lehet anyagi (energia) forma ido nelkul?) vagyis ebben az esetben a ter is veges kell hogy legyen, vagy helytelen a kezdeti feltetelezes.
viszont a meresek es az altaluk nyert tapasztalat nem azt bizonyitja hogy az ido vegtelen. mivel az anyag nem szakithato el az idotol, ezert inkabb azt kellene behatarolni hogy mit nevezunk a sajat ter-idonknek. mert ez a sajat ter-idonk lehet hogy veges, ugyanakkor mondjuk ugy hogy az "univerzum" ter-ideje lehet vegtelen.
a sajat idonkon azt ertem, amiota tagul az univerzumunk, persze ezen univerzum alatt az eddig megismertet gondolom. ez feltetelezi a nagy bummot.
lehetseges egy fraktal formaju elrendezodes is de ez kivul esik az altalunk megismerteken. es mi csak egy kis resze vagyunk a nagy egesznek.
-
Irasidus #79 Megérteni megértem, csak ez éppen nem objektív, elérkeztük a fantázia birodalmába, aminek a valósághoz semmi köze. Ezek szerint te csak a saját "ötleteidet" veszed figyelembe a tények, megfigyelések (szinte) teljes mellőzésével. Igaz?
Kezdve az olyan apróságokkal, hogy a "fényesség 1", miféle mértékegység ez és, hogy kapjuk meg? Nem tudjuk. Ezek utána - ki tudja milyen összefüggések után - önkényesen megfelezed a fény intenzitását, vagy éppen milliomod tizedestörtre aprózód a kezdeti fény intenzitását, a távolság négyzetével. Hogy hova lett a kezdeti fényerőssége, mennyisége nem derül ki. Mert neked így kényelmes... Egyébiránt meg nem veszed figyelembe, hogy a valóság nem ezt mutatja. Az energia megmarad, és a fény erőssége a fényforrás távolságától nem változik.
-
nnyiti #78 Bocs h bazdmegeztem de nagyon úgy tűnik, nem akarsz megérteni, hanem inkább belekötsz ilyen dolgokba h:
"Az meg csak hab a tortán hogy szerinted a fény elvész, és az energiamegmaradással mi lesz, he? "
"A fényerősség a fényforrástól mért távolságtól független,(középiskolás tananyag, nézd át. Sorry.)" - ki beszélt arról h a test fényerőssége változik?? én arról beszélek h a közelebbi csillag mennyivel látszódik fényesebbnek a mögötte lévő csillagtól...
"a Föld légköre, portalma erősen befolyásolja az átlátszóságot." - ja persze bocs, erre nem is gondoltam... de a te kedvedért akkor tegyük fel h az űrben vagyunk.
"Összeadni valamit nem egyelő a duplázással." te most komolyan hülyének nézel. azért mondtam duplázást mivel feltettem h két azonos erősségű lámpával játszadozunk... egyébként a sorozatos példámban összeadtam és nem dupláztam
a lényeg: a fényforráshoz az a mögött lévő fényforrásnak sosem a teljes fényessége adódik hozzá.
feltételezhetjük h a csillagok igen nagy távolságra vannak egymástól, tehát két egymás mögött lévő csillag a közelebbinek a fényességét nagyon kis mértékben erősíti erre tettem fel egy közelítő matematikai sorozatot. De így is mondhatom h életszerűbb legyen: 1+0,0002+0,000000034+0,00000000000069... stb. Ha ilyen mértékben adódnak össze, ez nem fog a végtelenhez konvergálni.
Csak az idegesít, h nem gondolod végig, hanem belekötsz a pontatlanságokba. -
Irasidus #77 Ha ingerűlt vagy attól még nem lesz igazad. Nem akarom ezt mondani, a Föld légköre, portalma erősen befolyásolja az átlátszóságot. Tehát nem fog kétszer fényesebben vakítani, bár én nem beszéltem neked a fényesősség duplázódásról az előbb az Olbers-paradoxonban. Összeadni valamit nem egyelő a duplázással. -
nnyiti #76 medve-bocs. te nem érted... figyelj: ha van két zseblámpád ami x erősséggel világít, magad felé fordítod az egyiket, a másikat pedig közvetlenül az előző mögött mondjuk 30 kilométerrel hátrébb magad felé fordítod, azt akarod mondani, h a közelebbi lámpa 2x fényességgel fog vakítani? ne vakíts már... az egy dolog ha fényerősség megmarad, de akkora távolságban NEM LÁTOM BAZDMEG, emhogy még 2xesére nagyítsa a fényerősségét a közelebbi lámpának... -
Irasidus #75 A fényerősség a fényforrástól mért távolságtól független,(középiskolás tananyag, nézd át. Sorry.), így a matematikai számításod megbukott. Ellenben azért nem ezt tapasztaljuk mert a fény egy része vöröseltolódást szenved (a csillagközi por és gázfelhők jótékony takaró hatásáról nem is beszélve) vagyis más hullámhosszú elektromágneses sugárzássá alakul át, ami ugye egy statikus (nem táguló) világegyetemben nem történne meg (illetve a por, és gázfelhők az elnyelt végtelen mennyiségű sugárzástól látható fényben izzanának). A fény intenzitása természetesen így is megmarad csak más hullámhosszon érzékeljük, bocs. -
nnyiti #74 Direkt idézőjelbe tettem, tudtam h azért is bele fogsz kötni. Nem vész el, csak átalakul, ahogy szokták mondani. Teljesen mindegy miért: a szétszóródás mértéke miatt, más testek takarása miatt stb. a lényeg h egy idő után nem lesz érzékelhető bizonyos technikai fejlettség mellett sem. Tehát van X csillag ami akkora messziségben van h szabad szemmel nem látható, de 1.0távcsővel igen. Ha szabad szemmel nézek fel az égre, akárhogy is nézem, nem fogom érzékelni az X csillagot - tehát az égboltnak az a pontja szabad szemmel sötét. Van Y csillag ami meg csak 2.0távcsővel látható. 1.0távcsővel már az égen sokkal több csillag látszik, de a technikai tökéletlenség miatt Y csillag helyén akkor is csak sötétséget látunk.
Most tegyük fel h van egy végtelen nagy felbontásba nagyító távcsövünk. Mit láthatunk:
1: mindenhol fényesség van - ebben az esetben nincs bizonyítva h végtelen v vége e a csillagok száma, mivel mindenhol fényesség van ha belenézünk a végtelenül nagyító távcsőbe, tehát nem láthajuk, h a látszódó csillagok mögött van e csillag.
2: nincs mindenhol csillag - szintén nincs bizonyítva, h végtelen v véges csillag létezik e, mivel ránézünk egy pontra, ami fényes, és amögött lehet végtelen sok csillag. Az egymás mögött lévő csillagok fénye valóban összeadódik, de nem a végtelen nagy fényességhez konvergál ez sima matematika:
van egy csillag amit látunk, legyen a fényessége 1. mögötte van egy csillag, mivel távolság van köztük, nem a teljes fényesség adódik hozzá, hanem a távolságtól függően kevesebb, a lényeg h kevesebb. Legyen mondjuk 0,1. Tehát az első csillag fényessége úgy h mögötte van a másik, összesen 1,1 es fényességgel világít. tegyük fel h a hátsó csillag mögött is van egy csillag, a távolság miatt viszont még az előzőnél is kevésbé kell hozzáadódjon, legyen 0,01. Tehát ha van egy csillag, ami mögött van egy csillag és amögött is van egy 1,11 lesz a fényessége a földről nézve! folytassuk a sorozatot, és egy egyszerű matematikai bizonyítással láthatjuk h a sorozat NEM a végtelenbe konvergál, tehát NEM BORÍTJA BE AZ EGET A FÉNYESSÉG attól h végtelen csillag van mögötte
Ergo senem bizonyítéka, senem cáfolata a Olbers paradoxon annak h végtelen sok csillag van e vagy véges. Ezért nem értem ez miért paradoxon... -
nnyiti #73 Na ez az utolsó OFF aztán hagyjuk ezt a témát, nem ide való:
"Én nem azt mondom, hogy dugjuk homokba a fejünket, csak azt, hogy legyünk tisztában azzal, hogy nem tudjuk, hogy kire/mire szavazunk"
Egyetértek, csak ezek a szavak az emberben tudatalatt azt sugallják, hogy nincs értelme szavazni, mert nincs idejük a köntös mögé látni ezért nem hozhatnak felelős döntést. Valószínűleg nem ez volt a célod, de én azért kihangsúlyoztam, h attól függetlenül amit mondtál (igazad volt), érdemes elmenni szavazni, akármennyire nem értünk hozzá. És azzal h siránkozunk, h az emberek többsége hülye és győzikén meg blikken nevelkedik, attól nem fog megváltozni semmi. -
djhambi #72 OFF
"Szóval függetlenül attól h mennyire ért hozzá az ember, én mindenképpen csak szorgalmaznám h ne dugjuk a homokba a fejünket csak azért mert "nem a szakterületünk""
Én nem azt mondom, hogy dugjuk homokba a fejünket, csak azt, hogy legyünk tisztában azzal, hogy nem tudjuk, hogy kire/mire szavazunk. Mert az ember alapfeltevésben valamennyire elfogadja azt, mit lát, vagy hall igaznak, és ez bizalom. A probléma ott van, hogy egy politikusban sem lehet megbízni, mert bár az lenne normális, hogy a mi érdekeinket képviseljék, és aki jobban képviseli a érdekeinket, az nagyobb támogatottságot kap. Valójában ez úgy valósul meg, hogy nem a teljesítményük alapján adnak nekik bizalmat a szavazók, hanem népszerűségi, szimpátia, "program" alapján. Ez pedig sok csalásra ad lehetőséget: bárki lehet népszerű, aki sokat ígér, vagy nagy tömegeket képes mozgatni érzelmi ráhatással, bármelyik párt lehet szimpatikus, amelyik új párt, és még nem sározták be a többiek, bárki írhat bármit a programjába, 4 év alatt úgyis elfelejtik, hogy mit ígértek, és ebből mit teljesítettek. Én mindig is csodálkozok azokon az embereken, akik hívei egy bármilyen pártnak (kb. 90%) mert az azt mutatja, hogy ezeket a dolgokat nem veszik észre, nem látják. Az a kérdés, hogy aki megtallja önmagát egy pártban, az tényleg a pártban találja meg önmagát, vagy a párt "imidzsében"? Senkivel sem találkoztam még, aki felvállalja, hogy Győzikét néz, mégis a legnézettebb műsorok egyike. Emberek milliói vesznek minden nap egy Blikket, csorgatják a nyálukat, hogy Liptai Klaudia harmadik gyereke fekete lett, és akkor vajon az apja Fekete Pákó? Az embereknek cirkusz kell, nem kenyér! Így lehet őket ide-oda rángatni a pártok között. Senkit sem érdekel ma a GDP, a nemzetközi megítélés, de fontoabb az, hogy ki mennyire buzi, és magyar, és hazug, és más jelentéktelen apróságok.
Így lehet őket ide-oda rángatni a pártok között. Senkit sem érdekel ma a GDP, a nemzetközi megítélés, de fontoabb az, hogy ki mennyire buzi, és magyar, és hazug, és más jelentéktelen apróságok.
Sokmindent megadék azért, hogy egy sör mellett őszintén elbeszélgethessek bizonyos politiusokkal (vagy egy hazugságvizsgálóra kötve a villamosszékben :D). Addig marad az, hogy a legkevésbé befolyásolató, hamisítható információk birtokában próbálom a legkisebb rosszt előnyben részesíteni, kizárni a sallangot. De azt is tudom, hogy a hozzám hasonló gondlkodású emberek kisebbségben vannak. -
Irasidus #71 Vagyis szerinted végtelen sok világító testet, végtelen nagy térben az ember nem látna... ühmm. Érdekes érvelés az is "amit valójában látsz" - mert igen ez pont azt mutatja hogy a fentebbi eset nem létezik. Az meg csak hab a tortán hogy szerinted a fény elvész, és az energiamegmaradással mi lesz, he? -
nnyiti #70 Ha olyan távolságon belül van, ami még érzékelhető, akkor igen. De egy bizonyos távolságtól már "elvész". Most gondolj bele: szabad szemmel látunk mondjuk 10^12 db csillagot, ha távcsővel nézem, csak akkor fogom látni a többi 10^10 csillagot, mert a szabad szemem nem érzékeli őket. Ha felteszem h vételen db csillag van akkor csak annyi változik, h az égbolt bármelyik pontjára nézel, lesz ott egy csillag, csak kellően fel kell nagyítani. Ettől függetlenül még nem muszáj látszódnia. -
Irasidus #69 "Öö egyébként ezt a Olbers paradoxont csak én nem értem? Most ha egy csillag végtelen messze van, akkor végtelenül kicsi a fénye a földön, nem? Nem látom át, ha végtelen csillag lenne miért kéne beborítsa az eget a csillagfény..."
1. Azért mert a fényük összeadódik. (lásd pl.: Androméda galaxis, tejút stb.) -
Irasidus #68 Ezek szerint nem árulod el mit értesz modell alatt csak használod a szót. A hipotézis nem modell.
"Arra gondoltam hogy a standard gyertyák abszolult fényessége állandó. Ez egy feltételezés. (Akkor is ha szőrszálhasogatásnak tűnik.) Ettől kezdve az összes "standard gyertyák állandó abszolult fényességén" alapuló következtetés az előbb említett feltételezésen alapszik.
Mielőtt félreértenél nem mondom hogy a standard gyertyák abszolult fényessége nem állandó."
Ezt illenék alátámasztani is. Egyébként távolságot nem csak így lehet mérni. (standard gyertya, geometrikus módszerek, és: )
A Hubble-törvény. A jelenleg ismert legnagyobb hatótávolságú módszer. Azon a megfigyelési tényen alapul, hogy a Világegyetem tágulása miatt a tőlünk egyre messzebb lévő galaxisok egyre nagyobb sebességgel távolodnak tőlünk. Ez a távolodás a Doppler-hatáson keresztül a galaxis fényének vörösödéseként jelentkezik, ami mérhető például a galaxis színképvonalainak az eltolódásából. A vörösödés mértéke (vagy a távolodás sebessége) a Hubble-törvény szerint arányos a galaxis távolságával, az arányossági tényező a Hubble-állandó.
Itt amint látod szó sincs standard gyertyákról.
"A wikipédiát meg azért idézgetem, mert jelen esetben igaza van."
wiki: "A fényesség független a távolságtól"
Ha akarom igaz, ha akarom nem. A meghatározás pontatlan.
Pont te okítottál ki hogy van látszólagos és abszolúlt fényesség. Tehát helyesen:
Az ABSZOLÚLT fényesség független a távolságtól, a LÁTSZÓLAGOS fényesség nem."
Ezzel nem tudom mit szerettél volna mondani de még mindig áll amit az előbb mondtam, rendere elfelejted az energiamegmaradás törvényét, és azt a tényt hogy a csillagok fénye összeadódhat. Lásd Tejút, Androméda galxis stb.
pl.: (ismereterjesztő formában, ha jól tudsz angolul akkor nehezebb, ás frissebb anyagot is belinkelhetek).:
elte
"Nem azt mondtam hogy a homogén világegyetemet az Olbers paradoxon miadt feltételezik, hanem azt hogy az Olbers paradoxonban a világegyetemet homogénnek feltételezik. (Remélem érezhető a kettő között a különbség.) És nem csak térben feltételezik homogénnak hanem időben is!"
Ok, kicsoda?
"A világegyetemet térben homogénnek feltételezni az egy dolog. De mond már el hogy időben miért is kellene homogénnek tartani a világegyetemet?"
Már elkezdtem írni, egy kis türelem, válaszolok erre is - csak ez hosszabb lesz. -
Amergin #67 Az, hogy feltételezünk egy negyedik dimenziót (dehát hol van?; bizonyíték?), hogy ezzel "megmagyarázzuk", hogy miért nincs "széle" az univerzumnak, az a problémát nem oldja meg, csupán eltolja egy dimenzióval felfelé (mert hát annak a 4 dimenziós alakzatnak is van széle...)
Persze hogy "kötekszem", de nem a kötekedésért önmagáért, hanem az igazsághoz szeretnék közelebb jutni és ezért kérdezek. Aki jobban tudja a dolgokat, az remélhetőleg meg is tudja védeni az álláspontját a felmerülő kérdésekkel szemben is. Egyébként olyan dolgokról vitatkozunk, amit nem is lehet definiálni
"Idő", "tér", "anyag" valójában nem tudjuk megmondani, hogy micsodák. Mérni, azaz bizonyos önkényesen kiválasztott részeiket egy másik részükhöz hasonlítani -ez minden, ami tőlünk telik egyelőre... -
philcsy #66 "2: Találj ki egy hipotézist, ami összeegyeztethető a tapasztalataiddal."
Tehát alkotsz egy matematikai modellt.
"3: A hipotézis segítségével adj előrejelzéseket."
A matematikai modelled segítségével kiszámolod a kísérlet várható eredményét, és a várható hibát.
Attól hogy nem mondod ki ezt csinálod, ne?
"Miféle következtetés feltételezés?" ???
Arra gondoltam hogy a standard gyertyák abszolult fényessége állandó. Ez egy feltételezés. (Akkor is ha szőrszálhasogatásnak tűnik.) Ettől kezdve az összes "standard gyertyák állandó abszolult fényességén" alapuló következtetés az előbb említett feltételezésen alapszik.
Mielőtt félreértenél nem mondom hogy a standard gyertyák abszolult fényessége nem állandó.
"A látszólagos fényességet meg félre értetted ha úgy gondolod hogy a "fény" útközben gyengül"
Te elolvastad azt amit írtam? #51-ben is kérdezted "Mond az a szó neked valamit hogy "Látszólagos"?" Képzeld mond. #49-be használtam is.
"A wikipédiát meg azért idézgetem, mert jelen esetben igaza van."
wiki: "A fényesség független a távolságtól"
Ha akarom igaz, ha akarom nem. A meghatározás pontatlan.
Pont te okítottál ki hogy van látszólagos és abszolúlt fényesség. Tehát helyesen:
Az ABSZOLÚLT fényesség független a távolságtól, a LÁTSZÓLAGOS fényesség nem.
"De tudok mást is idézni ha ez az óhajod, de az nem olyan olvasmányos - sok benne a differenciál egyenlet." Ne legyél rest.
"Még egyszer mondom nem az olbers paradoxon miatt tételezik fel a világegyetem homogenitását." Próbálom érthetően:
Nem azt mondtam hogy a homogén világegyetemet az Olbers paradoxon miadt feltételezik, hanem azt hogy az Olbers paradoxonban a világegyetemet homogénnek feltételezik. (Remélem érezhető a kettő között a különbség.) És nem csak térben feltételezik homogénnak hanem időben is!
A világegyetemet térben homogénnek feltételezni az egy dolog. De mond már el hogy időben miért is kellene homogénnek tartani a világegyetemet? -
nnyiti #65 http://edmroa.freehostia.com/vis.html
Én mindenkinek ajánlom, szerintem egy hétköznapi ember is meg tudja nagyjából érteni belőle, kb hogy is néz ki a negyedik dimenzió, főleg ha úgy képzeled el a negyedik dimenziót, mint az időt. Csak rá kell szánni egy kis 'negyedik dimenziót' :D És így mindjárt könnyebb elképzelni az önmagába forduló teret is. -
nnyiti #64 ö pf ne kezdjünk el politizálni hambi, mert már kaptál ezért felkiálítójeleket nem olyan rég :D
a politikás példád pont a lényegben veszti el értelmét, mert ezt a példát elvileg arra hoztad fel h az embernek megvannak a szakterületei, és más szakterületekhez nem nagyon tud hozzászólni, mert nem annyira ért hozzá. A politika viszont pont az a terület amihez bármennyire is nem értesz, hozzá KELL(ene) szólnod.
Mert amikor elmész szavazni, nem azért mész el, mert teljességgel értesz a szakmához. Pontosan ez a baj, az embereknek ezért csak a fele megy el szavazni, mert azt mondja "Én nem értek hozzá". Holott a lényeg nem azon van h most te tudod-e, hogy az xy politikus vajon igazat mond-e, vajon tényleg beválik-e a gazdasági modell amit hirdet, vajon csak azért manipulál h saját malmára hajtsa a vizet stb. Ezt nem az átlag embernek kell eldöntenie, hanem a politikusokra kell bízza.
Az ember azért megy el szavazni, mert az ominózus politikus megígért valamit, képvisel vmilyen értéket/érdeket, ami számomra szimpatikus, ami az én értékem/érdekem is Az pedig az alapműveltség része, hogy legalább annyit tudjunk, h körülbelül melyik párt mit ígér. Szóval függetlenül attól h mennyire ért hozzá az ember, én mindenképpen csak szorgalmaznám h ne dugjuk a homokba a fejünket csak azért mert "nem a szakterületünk"
Mellesleg
"Én igazat adok Magnul Pl-nek"
Magnul Pl konkrétan arról beszélt amire én válaszoltam, amivel te egyetértettél és arra fejtettél ki vmit.
Öö egyébként ezt a Olbers paradoxont csak én nem értem? Most ha egy csillag végtelen messze van, akkor végtelenül kicsi a fénye a földön, nem? Nem látom át, ha végtelen csillag lenne miért kéne beborítsa az eget a csillagfény... -
Irasidus #63 Soha nem értetem hogy kozmológiai számítások eredményeit amit csak hasonlatokkal lehet elmagyarázni, miért gondolják egyesek hogy így - ismeretterjesztő módon - megérthető a világegyetem. Elég nehéz a kérdésedre úgy válaszolni hogy közben ne tudj belekötni, mivel olyan ismerteink vannak ilyen téren - tehát a világegyetemről - amire nincsenek emberi kifejezések, csak hasonlatok. Viszont a hasonlatok önmagukban véve rosszak, mert csak hasonlat...
Próbáld meg két dimenzióban elképzelni az univerzumot, ami egy önmagába görbülő három dimenziós teste alkotna - gömböt. Nos ezen mint síkidom emberke bármilyen irányba indulsz el nem találnád meg a végét, holott magának a gömbnek van kiterjedése... most ezt próbáld meg ha tudod 3d-ben elképzelni, nekem nem sikerűlt. -
Irasidus #62 Miért kellene minden tudományághoz érteni? Én az általános műveltségről beszéltem, te láthatólag másról. Egyébként ha nem vagy tudományfilozófus, vagy részecskekutató akkor a te felfogásod szerint most éppen "mindenhez érten" próbálsz... Amit én is, te is elismerünk nem lehet. -
Irasidus #61 De értem a matematikai modellt, meg a többszintes modell közti különbséget is. Elmondanád te mit értesz modell alatt?
"Megnézném hogy a kisérlet elvégzése után mit csinálsz a kapott adatokkal. Mert hogy közvetlenül egy eredménnyel nem fogsz tudni semmit sem csinálni az biztos."
1: Vizsgáld meg valamilyen szempontból az univerzumot.
2: Találj ki egy hipotézist, ami összeegyeztethető a tapasztalataiddal.
3: A hipotézis segítségével adj előrejelzéseket.
4: Teszteld az előrejelzéseket kísérletekkel vagy további megfigyelésekkel.
5: Változtasd meg a hipotézist az eredményeknek megfelelően.
6: Folytasd a 3. lépéstől.
"Az Olbers paradoxon ettől függetlenül nem bizonyítja a világ végességét, mert a paradoxon máshogy is feloldható."
Persze azt még nem sikerült elmondani hogy... Nézd egy csillag fényét x távolságból észleljük, sok csillag fényét sokkal messzebbről is észleljük, mert a fényük összeadódik - nézd meg szabad szemmel pl.: az Androméda galaxist magát, viszont egyetlen önálló csillaga sem látható. A látszólagos fényességet meg félre értetted ha úgy gondolod hogy a "fény" útközben gyengül (persze ha porködön megy át akkor igen, de végtelen sok csillag összesugárzása (nem fénye) elnyelve már annak is izzania kéne. Az energiamegmaradás törvénye szerint.)
A wikipédiát meg azért idézgetem, mert jelen esetben igaza van. (De tudok mást is idézni ha ez az óhajod, de az nem olyan olvasmányos - sok benne a differenciál egyenlet.)
Még egyszer mondom nem az olbers paradoxon miatt tételezik fel a világegyetem homogenitását. De ha szerinted így van akkor nyugodtan idézz be egy tudományos cikket. Elolvasom.
"Hubble megfigyeléseiből levont következtetések maguk is feltételezésen alapulnak."
Miféle következtetés feltételezés? Ha doppler hatásra gondolsz, az jól elkülöníthető a galaxisok sajátmozgásától, illetve a gravitácíós potenciáljukból eredő vöröseltolódástól. -
djhambi #60 "Egyébként a tudomány csak azok számára átláthatatlan, vagy érthetetlen akik nem művelik, nem érdekel, nem veszik a fáradságot hogy legalább ismeretterjesztő szinten átnézzék..."
Kétféleképp lehet érteni a tudományhoz. Nagy vonalakban, mint a szabadbölcsész, vagy a műszaki menedzser, ak mindenhez ért egy kicsit, de valójábansemmihez sem ért, illetve úgy lehet érteni, hogy beleásod magadat, és egy teljes szakmát vagy szakirányt kitanulsz. Akkor a témánk olyan szakértője vagy, aki egy nem szakértőt bármikor lemos a föld színéről értelmes vitában.
Minden szakma ilyen, legyen az romanisztika szakso nyelvész, hídépítőmérnök, médiajogász vagy nemzetközi közgazdász vagy hajóács. Elképzelhető, hogy egymás szakmáit meg tudnák tanulni, ha foglalkoznának vele, de mivel nincs idejük, és nem foglalkoznak vele, nem rendelkeznek megfelelő tudásanyaggal. A tanulásra való képesség és a tudás nem ugyanaz, mert előtte azt meg is kell tanulni.
És ezt azért mondtam el, mert a felsőoktatásban sokbeképzelt ember van, aki mert csinálja, vagy netán diplomája is van, azt hiszi, hogy ő most mindenhez ért, és mindenkinél jobban tudja, és okosabb. Ez pedig egy sajnálotos emberi visszamaradottság, mondhatni hiányosság.
OFF
Vicces, de ilyen szakma is a politikai. No nem olyan érelemben, hogy ki kell tanulni. Van benne kommunikációs készség, retorika, különböző szociális statisztikákra épülő felépített szereplések, pszichológiai trükkök, a politika a manipulálás tudománya. És itt jön be a lényeg: mivel az emberek 99%-a nem szakmabeli, nem is lehet elvárni tőlük, hogy rájöjjenek ezekre a manipulációkra, hogy tudatosítsák magukban, hogy mit miért tesznek, miközben gondosan felépítenek a választókban illúziókat, hamis képeket. Sokszor egy bezéd tartalmilag teljesen érthetetlen értelmes ember számára, csak azt hallja ki, hogy egy percen belül már nyolcadszor mondák ki, hogy "magyar", vagy "jólét", vagy mindegy, különböző tartalomcsinált hívószavakkal manipulálnak, az emberekbe belesúlykolják az akaratukat, felépítenek egy várat, ami kívül szép, de belül a hétfejű sárkány lakozik. És mivel az átlagember nem szakmabeli, és csak a várat látja, mindegy, hogy mi van mögötte. Egyszerűen az emberek többségének nincs elegendő információja ahhoz, hogy egy döntést képes legyen meghozni. Az emberek leragadnak a külsőségeknél, a megjelenésnél, szimpátiánál, programoknál, hívószvaknál, és még ki tudja, hány manipulációnál. Én legalább odáig eljuottam, hogy értem, hogy ilyen van. Hogy a várfal mögé lássak, politikusnak kéne lenni. Ahogy nem értek a skandináv nyelvekhez, és nemértek a szobrászathoz sem. A politikusok olyanok, mint a kortárs művészek, akik rajzolagtnak vonalakat, és ők maguk között értik, hogy mi azoknak a vonalaknak az értelme, tartalma, az emberek pedig a kiállításon azt látják: de szép színek, biztos ezért jó a kép. Az embereknek pedig nincs elég információjuk ahhoz, hogy felfedezzék a festmény valódi célját.
Ha célról beszélünk, talán felvázolhatnám, hogy genetikai okokból az embert mi is motiválja: a hatalom (pénz, erő, nőstényekért vívott harc, az uódok életfeléteeinek javítása) és a legkisebb energiára törekvés (fölöslegesen senki sem töri magát). A kettő együtt valahogy a politika mocskos motivációja. -
Amergin #59 0,999... = 1
Ha az univerzumban az idő és a tér a végtelenhez tart (márpedig jelenleg úgy tűnik), akkor az univerzum véges vagy végtelen? Állítólag az univerzum "sík" azaz nem görbül önmagába, hiszen a benne lévő tömeg gravitációja nem képes lassítani a tágulást. Milyen akkor tehát az alakja? Hogyan kell elképzelni az Univerzum Alakját, polgártársak?
Nem három dimenziós. Igen? Akkor mennyi?
Három dimenziós. Nocsak! Akkor bizonyára széle is van...
-
philcsy #58 Hubble megfigyeléseiből levont következtetések maguk is feltételezésen alapulnak. -
philcsy #57 Én csak az mondtam hogy az Olbers paradoxonban feltételezik.
Az Olbers paradoxon ettől függetlenül nem bizonyítja a világ végességét, mert a paradoxon máshogy is feloldható. -
philcsy #56 "... Olbers erről beszélt."
Nem kéne orba-szájba wikire hivatkozni ugye. -
philcsy #55 "Szerintem te nem érted a modell fogalmát. Milyen modellről beszélsz?"
Matematikai modellről. Ha ezt nemérted...
"A kísérleti előtt kell egy elmélet (nem modell) amit tesztelsz..."
Megnézném hogy a kisérlet elvégzése után mit csinálsz a kapott adatokkal. Mert hogy közvetlenül egy eredménnyel nem fogsz tudni semmit sem csinálni az biztos. -
MacropusRufus #54 "...köztük a tömegért felelős Higgs-bozon is W-bozonokká bomlik...."
nem értem. Ha a Higgs-bozon ad tömeget, akkor ha lebombil, a tömeg megmarad?
Akkor mi is ez a Higgs-bozon? Hogyan tud valami a semminek tömeget adni, úgy hogy lebomlás után a tömeg megmarad? Azért a semmihez, mert ha valaminek nincs tömege az gy.k. nem is nagyon létezhet (mindennek van tömege, akármilyen picike is, még az atomnak is meg az atomot alkotó elemeknek is és a zőket alkotóknak is stb...)
-
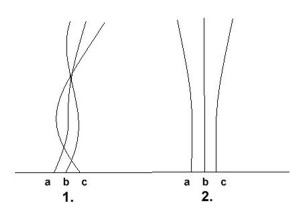
Irasidus #53 Hubble megfigyelései arra engedtek következtetni, hogy az Univerzum rendezett struktúrákkal rendelkezik, vagy legalábbis olyannak látszik. Ha kiválasztunk néhány önkényes világvonalat, amelyek mondjuk galaxisokhoz tartoznak, azok kétféleképpen nézhetnek ki.
Az 1. esetben egymást metsző,
a 2. esetben rendezett mozgású galaxisok világvonalai láthatók. Ezt a második esetet fejezi ki a Weyl-posztulátum: konstruálhatók olyan térszerű hiperfelületek konstans világidőknél, hogy a rajtuk átmenő világvonalak merőlegesek a hiperfelületre...
Stb. -
Irasidus #52 Nem Olbers paradoxonja miatt feltételezik a világ homogenitását. -
Irasidus #51 Szerintem te nem érted a modell fogalmát. Milyen modellről beszélsz?
A kísérleti előtt kell egy elmélet (nem modell) amit tesztelsz...
Mond az a szó neked valamit hogy "Látszólagos"? A csillagok látszólagos fényességének mértékegysége a magnitúdó. Minél fényesebb egy adott csillag, annál kisebb a magnitúdó értéke. A magnitúdó logaritmikus mértékegység: ha két csillag látszólagos fényessége között 1 magnitúdó különbség van, akkor az egyik csillag 2,512-szer fényesebb a másiknál. A látszólagos fényesség nem utal a csillagok valódi fényességére. Egyes halvány csillagok látszó fényessége azért kicsi, mert nagyon távol vannak a Földtől. Ezért a csillagok valódi fényességét az abszolút fényesség adja meg, amely a csillag 10 parszek távolságból megfigyelhető látszólagos fényessége. Olbers erről beszélt. -
philcsy #50 Ja és ha megfigyeled az Olbers paradoxban feltételezik a világ homogenitását("egyenletesen elhelyezkedő csillagot tartalmaz"). A világ viszont a tapasztalatok szerint nem homogén. Vannak nagy üres területek.