1111
Elgondolkodtató matematikai, logikai feladatok, feladványok
-
 #230
#230
Kaptam egy "bunkó" nevű mp3-at, amiben 4 kérdést tesznek fel és ha már egyre tudod a választ, akkor nem vagy bunkó! Nagyon jó. Igazából nem bunkó vagy, ha nem tudod, csak ennek nevezték el, nemtom miért. Privizzen rám egy e-mail címmel az, akinek kell. Vagy itt is feltehetem a kérdéseket, de az egyik olyan, hogy fórumban lehetetlen jól megcsinálni, de a többit is inkább hallani jó.
Az e-mail címekkel nem fogok visszaélni
-
 #229
#229
Igen, igen. Imádom Örkény egyperceseit:) -
 #228
#228
Szabályos futballkapu, benne szabályos kapussal, aki a látogatóknak a 11-es
vonalról leadott lövéseit játszi könnyedséggel védi, jeléül annak, hogy
végeredményben minden lövés védhető.
De néha-néha, ha arra téved egy válogatott csatár (mint egyszer Jaka II. az
öccse esküvője után), hirtelen csönd lesz a futballkapu körül. Hiszen
köztudomású, hogy egy válogatott csatár védhetetlen tizenegyest is tud rúgni,
másfelől viszont egy ilyen kivételes képességű kapus a védhetetlen lövést is
védeni tudja. Ők tehát már nem emberi szinten fognak összecsapni, hanem odébb,
képességeink határán túl.
És mi történik most? A lövés (mint annak idején Jaka II. süvítő ballábasa is)
mindig erős, és jól irányzott, de az a valami, az a kis plusz, a végtelenség
akarása mégiscsak hiányzik belőle. A kapus pedig ugyanolyan könnyedén, mint
máskor, ezt a nagy lövést is vetődve kivédi.
Utána, alig észrevehető mosollyal, odabiccentenek egymásnak. -
 #227
#227
most megkerestem, neten is fent van: Örkény István: A Vidám Parkban :) -
 #226
#226
Húú. Ez most jó kérdés, de azt hiszem, hogy "a cirkuszban". De ebben több rövid nem összefüggő történet van. De mondom, nem biztos a neve sem, és az sem, hogy ebben van. -
 #225
#225
Örkény rulz. Mi ennek a művének a címe? -
 #224
#224
Örkény Istvánnak van egy nagyon hasonló egyperces novellája. Ott egy nagyon jó focista, aki tud védhetetlen hetest lőni és egy kapus, aki a védhetetlen lövést is védi. A focista belövi, majd a végén alig észrevehetően odabiccentenek egymásnak....
Érdemes elolvasni -
 #223
#223
hat igazabol ez nem eletszeru, igy baromsag, dehat vegulis ha nagyon el akarjuk kepzelni, akkor egyszeruen nekimegy, es visszapattan rola talan -
 #222
#222
egyszer még kisiskolás koromban vmi ilyen paradoxont hallottam: mi történik akkor ha az összetörhetetlen,megállíthatatlan,eltéríthetetlen vonat nekiütközik egy kidönthetetlen,elferdíthetetlen, megmozdíthatatlan oszlopnak? -
Dougie #221 jaja, ez is benne van a wikipédiában, ez a születésnap-paradoxon
link
ami egyébként szintén nem is paradoxon, ugyanis nincs ebben semmi ellentmondás, inkább csak meglepő, de igaz -
 #220
#220
Igen,nem azért mert ott mi választunk és nem biztos h rosszat(kecskét) nyitunk ki?
Amúgy meg olvastam nemrég valami olyat,hogy ha tetszőlegesen kiválasztunk 23 embert,akkor 50% az esélye annak,hogy közülük ketten egy napon születtek. 60 embernél ez nagyjából 99%....ez nem feladvány,csak valószínűségszámítás. De érdekes. -
 #219
#219
igen, csak kevesbe hatekonyan -
 #218
#218



-
 #217
#217
most azon gondolkodom h ezt az áll az alkuban lehetett-e volna alkalmazni...:) -
Dougie #216 akkor ne három ajtóban gondolkodj, hanem legyen mondjuk 10
az elején választasz egyet, ha egy jó van, akkor 10% az esély hogy jót választasz - akármi trténik ez után az 10% marad, mert az az összes közül választottad, tehát a többi 9 együttvéve 90% (külön-külön persze ott is 10, de együtt 90% hogy azok között van) eddig gondolom világos
na most, ha elveszel a 9 fennmaradóból 8-at, akkor az az egy ami közülük maradt 90% hogy a jó, mert azok együttese 90 volt, tehát mindenképpen váltani kell a legvégén -
 #215
#215
"Az, hogy a műsorvezető ezek után kinyitja a másik két ajtó egyikét, megmutatván egy kecskét, nem változtat ezeken a valószínűségeken, továbbra is 1/3 az esélye, hogy az elsőre választott ajtó mögött van az autó."
ezt most én sem értem :) Az ajtónyitás után miért marad 1/3 az esélye az autóra, amikor csak kettő közül választ. Igaz hogy eredetileg 1/3-ad volt az esélye, de az már nem 1/3-ad lesz mikor kinyílik az ajtó, szóval most csak így tudok rágondolni :) A kecskés ajtót már kinyitották, tehát azt nem tudja a játékos "újra kinyitni". szóval? -
 #214
#214
Ne kelljen már erre is egy C programot írnom :D -
Thanatos #213 bazz és igy elolvasva tényleg, még ismertem is ezt a feladványt csak nem emlékeztem rá, basszus :D -
 #212
#212
a montihólt viszont butaságnak tartom :S
1. ajtó 2. ajtó 3. ajtó Monty kinyitja Ha váltunk
kecske kecske autó a 2. ajtót nyerünk
kecske autó kecske a 3. ajtót nyerünk
autó kecske kecske valamelyiket vesztünk
mi az hogy kinyitja valamelyiket :\ ugyanúgy fel kéne írni hogy kinyitja a másodikat, vesztünk, kinyitja a harmadikat, vesztünk. és máris 2-2 a győzelmek és vereségek aránya, tehát 50-50%.... -
7evenb #211 akkor jöhet 4D-ben:) -
 #210
#210
nekem jónak tűnik végre :) -
7evenb #209 ha ez sem jó, feladom... -
7evenb #208 -
 #207
#207
Lassan elárulhatnád...
;D -
 #206
#206
gondoltam azért szenvedsz, mert már 3D-ben is megoldod lassan...:D -
7evenb #205 azért annyira nem szenvedek:)
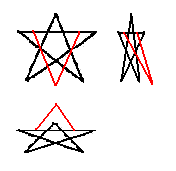
2d-ben szerintem nincs ilyen. 1 egyenes max 2-vel növeli a háromszögek számát. -
Easy Rider #204 ha 3dben van akkor nem metszheti a pentagrammát, szóval csak 6 háromszöged van! -
 #203
#203
omg, naon szenvedsz vele:D -
 #202
#202
Elolvastam Wikipédián és most kezdem érteni :) Nagyon érdekes. -
Dougie #201 igen ez az, ugyanez magyarul rövidebben
egyébként a dolog másik verziója is érdekes:
Ebben a változatban ugyanúgy három ajtó van, egy autó, két kecske, de ezúttal két játékos választ egy-egy ajtót. (Nem ugyanazt.) A következő lépésben az egyik játékos, aki kecskét választott, kiesik, Monty pedig kinyitja az általa választott ajtót, majd felteszi a bentmaradó játékosnak a szokásos kérdést. Ha mindkét játékos kecskét választott, Monty véletlenszerűen dönti el, hogy ki fejezi be a játékot. (Természetesen erről a játékosok nem tudnak.) A kérdés ezután ugyanaz: érdemes-e a bennmaradt játékosnak váltania?
(és ebben az esetben nem érdemes váltani) -
 #200
#200
azaz, monty hall -
 #199
#199
Mondjuk szerintem annyira nem elgondolkodtató, mindinkább érdekes.
http://en.wikipedia.org/wiki/Monty_Hall_problem
Itt van a leírás. -
 #198
#198
kocsis-kecskés feladványra okoskodas
SPOILER! Kattints ide a szöveg elolvasásához!Ez a nemtommi-paradoxon. A választás előtt 1:3 volt az esélye, hogy az autót választja, 2:3, hogy kecskét választ. Miután ki lett nyitva a 3. ajtó, és kiderült, hogy kecske van mögötte, annak esélye, hogy -és itt jön a lényeg- az autót választotta, továbbra is 1:3, hiszen a tény, hogy 3 ajtóból 1et válaszott, továbbra is megmarad; illetve annak, hogy az autó valamelyik csukott ajtó mögött van, 1:1 az esélye még mindig, hisz mindenképp csukott ajtó mögött van, ez érthető. Viszont ezekből látszik, hogy az ő ajtajának 1:3 az esélye, az összes ajtónak 1:1, tehát a második ajtónak 1:2höz, emiatt érdemes váltania. -
 #197
#197
Igen. -
 #196
#196
Hát először is az eredeti kérdés az volt, hogy hány háromszög van az ábrán. Elkezdtem számolni és jájöttem, hogy több, mint 10 és kiagyaltam, hogy a feladat feladója valószínűleg olyanra gondolt, amiben nincsen másik vonal (kis háromszög). Ezért hát elkezdtem ilyenen gondolkozni és be is szúrtam egy képet, és kiderült arról, hogy nem jó. Nem azért, mert rosszul értelmeztem (az egyébként először rosszul is megfogalmazott feladatot), hanem én is (mint páran mások is) rosszul számoltam össze és egy négyszöget háromszögnek néztem (#107).
Egyébként nem Zrínyin, hanem sima megyein lettem első. De szerintem nem ettől függ, hogy egy fórumban vissza tudom olvasni a hozzászólásokat. Vagy igen??? -
7evenb #195 :D -
 #194
#194
Azért mert ha a kocsit elviszi a műsorvezetőnek a kára? =P Mert a műsorvezetőnek kell a kocsi és ezért kecskét akar neki adni =P -
 #193
#193
Neked van ilyenre időd? :D:D:D -
Dougie #192 most ha azt mondom hogy nem jó a válaszotok, akkor azzal már elárulom hogy igen
oké, szóval a kérdés az, hogy miért előnyös ha vált (mert előnyös) -
7evenb #191 3D-ben: