4415
Matematika feladatok
-
hiper fizikus #4415 Sziasztok !
1. Ha megfenyítünk egy gyereket a rosszaságáért, akkor egyáltalán nem mindegy, hogy hová ütünk neki !
2. A diákot azért büntetni, mert nem ismeri a tanulás módszerét vagy mert akarta de nem tudta megtanulni elemi pedagógiai hiba !
3. A kommunizmus idején az antikommunisták gyerekeit megverték az iskolában a diákok és a tanárok egyaránt; tudom mert velem is ezt csinálták, de neveket nem említhetek, mert kimoderálnának ! Úgy hogy én kívülre kerültem a közösségből, és megállapítottam, hogy kívületek jobb mint veletek; páá !
4. Egyébbként én imádom a matematikát -> a racionalizmust és az empírizmust !

-
kreon81 #4414 sziasztok :)
-
hiper fizikus #4413 néhány vicc link a tudományhoz:
http://www.t-es-t.hu/humor/vicc.htm
http://members.iif.hu/visontay/ponticulus/rovatok/humor/viccek.html
https://liked.hu/elet/szorakozas/21-tudomanyos-poen/

-
#4412
matek poén gif
SPOILER! Kattints ide a szöveg elolvasásához!
-
 #4411
#4411
Egy kicsit off, de lehet örül majd neki innen valaki
latex-math-in-office -
 #4410
#4410
Ó bakker, ja hogy így kéne. Köszi szépen, megvan akkor (azért leellenőriztem..) -
cylontoaster #4409 P(X=1)=0.2975
P(X=2)=0.2678
P(X=3)=0.1607
----------
P(1<=X<=3)=0.726
Nem tudom ez így segít-e, vagy ennél több kéne. Online kalkulátorral számoltam ki... -
 #4408
#4408
Hali!
Kéne egy kis help Poisson eloszlásos feladatban.
Lambda(10perc) = 1.8 =v.é. -> szórás 1.34
Feladat:
Mi a vszg-e annak, hogy a 10 perc alatt érkező ügyfelek száma legfeljebb 1 szórásnyival tér el? (0.7260 a megoldás)
Nem csak a P(3.14>#>0.46) t kellene kiszámolni? Mert nekem erre nem jön ki. Akkor mégis hogy kell kiszámolni? -
 #4407
#4407
Köszönöm! Ebben a nyomatéki egyensúlyi egyenletben tudnál esetleg segíteni? -
 #4406
#4406
Hogy mi?
Egy egyensúlyban levő libikóka bármilyen szöghelyzetében egyensúlyban van (vagy ha úgy tetszik: "egyensúlyban marad").
A forgáspontra felírt nyomatéki egyensúlyi egyenletből fog az kijönni, hogy mindkét oldalon az alfa szög koszinusza jelenik meg, amivel egyszerűsítve egy olyan egyenlet lesz, ami alfától nem függ és mindig egyenlő. -
 #4405
#4405
Sziasztok!
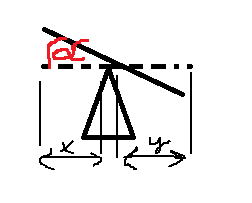
A képen egy libikóka látszik, X és Y egyforma hosszúságú, és a szaggatott vízszintesben van, a másik pozíció tetszőleges eldőlést mutat az egyik irányba. Hogyan lehetne a pirossal jelölt alfa szöget levezetni X ből és Y ból? semmi nincs megadva, se hosszúság, se magasság, se semmi.
Köszönöm! -
 #4404
#4404
7/2, 9/2
19/2, 7/2
Utoljára szerkesztette: ZilogR, 2017.03.01. 22:11:59 -
kl24h #4403 Ki nem tudja megoldani? -
 #4402
#4402
Ha van általános matek topik, akkor bocsi :)
https://www.reddit.com/r/math/comments/5vbjkr/what_books_in_math_written_in_the_past_20_years/
Top komment:
Galois groups and fundamental groups by Tamas Szamuely. A lovely book written in a clear style. -
 #4401
#4401
:))
-
dopli #4400 Köszi a segítséget, a hozzászólásodnak köszönhetően megoldódtak a problémáim. Egyébként nem egyetlen műveletre gondoltam, hanem műveletegyüttesre. Pl: (log17(n))^7,5+23=x
Ez a képlet pl n=38-885 -re olyan x-eket ad, amelyek esetében az x/n arány 0,612 és 0,816 közé esik -
TZson #4399 Közben rájöttem, hol a hiba a 2)-ben: nem log_x(n)-nek kell 0,6 és 0,7 között lennie, hanem az n-szeresének. Tehát az előzőeket javítva:
0,6<ln(n)*n/ln(x)<0,7
0,6*ln(x)<ln(n)*n<0,7*ln(x)
A két egyenlőtlenség:
ln(x)<ln(n)*n/0,6
ln(n)*n/0,7<ln(x)
Mivel ln(n)*n a vizsgált tartományban monoton, ezért elegendő a határakon megnézni.
ln(x)<38*ln(38)/0,6=230,3804...
ln(x)>855*ln(855)/0,7=8245,988...
De ennek továbbra sincs megoldása. -
TZson #4398 Hali!
Nem teljesen értem a kérdésben a "matematikai művelet" kifejezést.
1)
Ha tetszőleges függvényt értesz alatta, akkor például az r/n=0,65 egyenlet átrendezésével kapott r=n*0,65 szabállyal adott függvény jó lesz, azaz f(n)=n*0,65. Ennek az eredménye valós lesz, hiszen egész szám racionálissal szorozva racionális marad.
2)
Ha a középiskoláig tanított műveletekre gondolsz, akkor például egy logaritmus megfelelő lehet, hiszen ennek az értéke is mindig valós. Az a kérdés, hogy milyen alapú logaritmust vegyünk hozzá. Legyen a logaritmus alapja most x, és kicsit átalakítjuk, hogy számológéppel könnyebben lehessen számolni:
log_x (n)=ln(n)/ln(x)
Ennek kell 0,6 és 0,7 között lennie, azaz
0,6<ln(n)/ln(x)<0,7
Feltesszük, hogy ln(x) pozitív (ha nem az, akkor nem is oldható meg, hiszen ln(n) mindig pozitív lesz), ezért átszorozhatunk vele:
0,6*ln(x)<ln(n)<0,7*ln(x)
Olyan x kell nekünk, amire a fenti egyenlőtlenségek teljesülnek 38<n<855 esetén. Ezek alapján tehát
0,6*ln(x)<ln(n)<=ln(38) mivel ez a legszigorúbb
és
ln(855)<=ln(n)<0,7*ln(x)
Azt kapjuk tehát, hogy
0,6*ln(x)<ln(n)<=ln(38)
ln(x)<ln(38)/0,6=6,0626...
A másik oldal:
ln(855)<0,7*ln(x)
9,644=ln(855)/0,7<ln(x)
Ilyen x tehát nincs, bár lehet, hogy valahol elszámoltam...
3)
Ha programozni akarsz és nem kell, hogy r és n számok szinkronban legyenek egymással, akkor egy RAND() függvényt lehet használni. Ez általában 0 és 1 közötti számokat választ egyenletes eloszlás szerint. Ami nekünk most kell:
f(n)/n=c
f(n)=n*c
ahol c 0,6 és 0,7 közötti random szám, tehát az előző RAND() utasítást kell kicsit átalakítani:
c=RAND()/10+0,6
Ezzel már jó értékeket fogsz kapni. -
dopli #4397 Hali!
Olyan matematikai műveletre van szükségem ami egy n (38<n<855) természetes számból egy r valós számot csinál, de úgy, hogy az r/n arány 0,6-0,7 között legyen. Hogyan fogjak hozzá? -
 #4396
#4396
:) nagy a pangás
Utoljára szerkesztette: Jim Morrison, 2016.11.19. 23:16:15 -
 #4395
#4395
Jally... Az ennek a lényege, hogy postoljad és az oldalra mutató link keletkezzen egy közösségi oldalon.
Megérett a világ egy RESET-re.
Akinek mond valamit a KMBK, az tudja, hogy negyedikben már sejtautomatákat színezgettünk négyzetrácsos papíron és számítógép még sehol se volt... Ahhoz képest most egy okádék, amit tanulnak a diákok. -
Gascan #4394 remelem nem sokat idozol ilyen cikkek olvasasaval :D -
Koppixer #4393 Ön meg tudja oldani ezt a 2. osztályosoknak szánt feladatot?
"A 19 leszálló ugyanis állítólag csak egy elterelés, hiszen az teljesen mindegy mennyien szállnak le a vonatról... "
lol :D -
Thibi #4392 Az x^6 az x^3 négyzete, az 1 pedig az 1 négyzete, (a^2-b^2)=(a+b)(a-b) alkalmazható -
Madi92 #4391 Help.
Naaagyon régen nem matekoztam már és már ilyen alap dolgokat sem tudok megoldani. :S
Egy egyszerűsítést kell csak, de már nem tudom, hogyan álljak neki.
(x^6-1)(x^3+1)/x^3-1
Tudom, hogy nagyon egyszerű, de ez van. :D -
Koppixer #4390 Így törd fel a Puttó algoritmusát -
kjhun #4389 Ez jó?
SPOILER! Kattints ide a szöveg elolvasásához!http://moldan.hu/page.php?3 -
 #4388
SPOILER! Kattints ide a szöveg elolvasásához!Hali srácok, nemtudom hogy, szabad e ilyet kérdezni, de valaki nemtudja hogy honnan tudnám tölteni, vagy csak online megnézni ezt a könyvet?, csak javitókulcsot találtam hozzá
#4388
SPOILER! Kattints ide a szöveg elolvasásához!Hali srácok, nemtudom hogy, szabad e ilyet kérdezni, de valaki nemtudja hogy honnan tudnám tölteni, vagy csak online megnézni ezt a könyvet?, csak javitókulcsot találtam hozzá
Utoljára szerkesztette: Jani Hun, 2014.12.14. 13:54:54 -
TZson #4387 Ezt nem tudtam, köszi az infót! :) -
 #4386
#4386
"Sőt, még a fenti egyszerűsítés is lényegtelen a gép szempontjából, mert a hatványozást is szorzásként végzi, ha jól tudom"
Természetesen nem egymás után végzi el annyiszor a szorzást, hanem a hatványozást célszerű logaritmussal szorzásra visszavezetni:
c=a^b számítása: ln(c) = ln(a^b) = b×ln(a), innen: c=exp(b×ln(a)). Ezzel tipikusan sok baj van, mint például pontatlan, mert van benne ln() és exp() is, amik általában korlátozott pontosságú rutinnal vannak megoldva, emiatt pl. régebbi számológépeken a 3^3 nem volt egyenlő 27-tel. -
Gascan #4385 igen, erre jutottam en is .. koszi :) -
TZson #4384 Attól függ, mit értesz időigényesség alatt. :)
Ha kézzel (számológéppel) számolsz, akkor lehet, hogy egyszerűbb, ha az azonos százalékokat csoportosítod, és egyszerre osztasz le velük.
Pl. ha az első két évben 3% a kamat, a 4., 5. és 6. évben 7% és a 7-10. években meg mondjuk 5%, a végén legyen mondjuk 200, akkor egyszerűbb az azonos százalékokkal egyszerre leosztani.
Azaz ahelyett, hogy:
200/1.05/1.05/1.05/1.05/1.07/1.07/1.07/1.03/1.03
érdemes úgy számolni, hogy:
200/((1.05)^4)/((1.07)^3)/((1.03)^2)
Mivel a szorzás kommutatív, ezért ha nem egymás után vannak az azonos százalékok, akkor is lehet így csoportosítani őket.
Ha arra irányult a kérdésed, hogy algoritmikus szinten meg lehet-e oldani gyorsabban, akkor jelen tudásom szerint nem. (Sőt, még a fenti egyszerűsítés is lényegtelen a gép szempontjából, mert a hatványozást is szorzásként végzi, ha jól tudom). -
Gascan #4383 sziasztok .... a kovetkezo szazalekkal kapcsolatos kerdesem lenne
alap 100
1. evben 2% kamatot kapsz = 102
2. evben 3% kamatot kapsz = 105 (102 * 1.03%)
milyen egszeru modon tudom megtudni, hogy mennyi volt az alap ertek a 0. evben ha nem ismerem?
visszaosztassal oldottam meg ... 105/(1.03%)/(1.02%) ...
ha tobb evrol van szo es valtozo szazalekokrol akkor ez eleg idoigenyes... tud valaki egy egyszeru kepletet erre vagy nincs mas megoldas? -
TZson #4382 Talán kicsit "elegánsabb", és ha sok Y érték van megadva, akkor gyorsabb is, ha átrendezzük az egyenletet:
y=72-x^2/18
Mindkét oldalból kivonunk 72-t:
y-72=-x^2/18
Beszorozva (-1)-el (ilyenkor az előjelek változnak):
72-y=x^2/18
Beszorozva 18-al:
1296-18y=x^2
Gyököt vonva (itt kell vigyázni, mert ugyebár egy pozitív szám két számnak is lehet a négyzete):
x1=+gyök(1296-18y)
x2=-gyök(1296-18y)
Pl. 64 esetében:
x1=gyök(1296-18*64)=gyök(1296-1152)=gyök(144)=12
x2=-gyök(1296-18*64)=...=-12
Kicsit bonyolultabb, de hosszútávon megéri ezt a módszert alkalmazni, mert:
1) nem kell mindig egyenletet rendezni, hanem csak beírod a számológépbe, és kijön.
2) nehezebb példákhoz is jó gyakorlás ;) -
 #4381
#4381
Köszi már már értem, végre .. nem is tudom, hogy nem jutott eszembe, hogy az Y helyére helyettesítsem be a 64-et .. szégyen .. 
-
Pio #4380 Semmi gond, azért van ez a topik, hogy segítsünk. :)
Ha y van megadva, akkor egyszerűen azt helyettesíted be:
64=72-x^2/18 |-72
-8=-x^2/18 |*(-18)
144=x^2
x=+-12 -
 #4379
#4379
Tök egyszerű feladat, de kicsit tanácstalan vagyok, sehogy sem jön ki a dolog. Matekból sosem voltam pro.
Adott egy táblázat,
x|0|6|__|18|__|__|__|
y|_|_|64|__|40|22|0|
És van egy egyenlet :
y=72 - x^2/18
Na most az világos, hogyha 0 és 6-ot behelyettesítem, akkor az ugye,
y=72 - 0^2/18 az y=72
ha
y=72 - 6^2/18 az y=70
De ha az Y van megadva, akkor mi a teendő, mit és hogyan ? Kicsit hülyének érzem magam, mert nem bírok rájönni, tök egyszerű tisztában vagyok vele, de segísetek kicsit, hogy eltudjak indulni .. Köszi!
Utoljára szerkesztette: V43 1105, 2014.09.10. 19:52:10 -
DRFlame #4378 Ezt a fa modellezést is többnyire a 4370-re írtam, hogy miért is nem csak 15 (ami inkább 16) féle szám lehet 1 pozíción a számolásunkban. -
DRFlame #4377 Az a baj, hogy te alapból rendezve akarod megszámolni, ami nem hülyeség, csak úgy sokkal nehezebb modellezni.
Mert ha azt mondod, hogy az első szám 1, akkor ha tovább ágaztatod a lehetőségeket akkor sokkal több ágad lesz, mint ahol az első ágadnál a 15 vagy akár 16 szerepel. Ha az első szám nálad 16 onnantól kezdve a többi szám adott (17,18,19,20), vagyis nem ágazik tovább, míg ha az első szám 1, akkor a 2. pozíción lehet 16 féle lehetőség (2-17) és a további ágak is attól függnek, hogy az adott pozíción mi a szám. Ez egy viszonylag szabálytalan fa lesz.
Míg ha abból indulsz el, hogy a sorrend is számít a húzásnál, akkor sokkal szabályosabb a fa. Első résznél 20 fele ágazik, aztán mindegyik további 19, aztán 18 stb... fele, attól teljesen függetlenül, hogy adott pozíción mi a kihúzott szám. Így végül kijön, hogy a fa 20*19*18*17*16 fele ágazik. Tehát ennek a fának végül 1.860.480 ága lesz. És utána tudunk azzal foglalkozni, hogy ezt 120-asával (5*4*3*2*1) be tudjuk csoportosítani a sorrend miatt, és így jön ki végül a 15.504.
A "te fádnak" már eleve annyi vége van, amire kiváncsi vagy, vagyis 15.504, csak éppen sokkal szabálytalanabb, nem homogén. Minden szinten az adott ágon szereplő számtól függ, hogy hány fele ágazik tovább, így nem tudsz úgy szorzást használni a számolásodhoz, mint a másik fánál. Vagyis ez a modell nem használható. Legalábbis messze nem olyan hatékonyan, mint a másik megközelítés.
Ezért van az, hogy akár számít a sorrend akár nem, a modellezéshez abból érdemes kiindulni, hogy számít. Aztán később lehet egyszerűen osztani ha nem számít a sorrend.
(Ha kombinatorikai képleteket használunk és nem modellezgetünk akkor természetesen érdemes egyből a megfelelő képletet választani attól függően hogy számít a sorrend vagy sem)
Tehát ha sorbarendezi a rendszer, akkor nem számít a sorrend, vagyis 15504 a megoldás. Ha pedig a sorrend is számít, akkor 1860480. -
 #4376
#4376
sorrendbe rakni sry 
így még kevesebb a variáció.