Hunter
A világűrben bizonyíthat az E=mc2
Az első atombomba felrobbantásával a világ megtanulta a fizika egyik legfontosabb és legnagyobb következményekkel járó alapelvét, a tömeg-energia ekvivalenciát, amit elsőként Albert Einstein demonstrált speciális relativitás elméletében, a mára már ikonikussá vált E=mc2 egyenletével, melyben E az energia, m a tömeg és c a fény sebessége.
Bár azóta a fizikusok számtalan kísérlettel és számítással igazolták Einstein egyenletét, és számos technológia, köztük a mobiltelefonok és a GPS navigáció is függ tőle, az Arizona Egyetem fizikus professzora, az orosz származású Andrej Lebegy nagy vihart kavart azzal a feltevésével, mely szerint az egyenlet nem minden körülmények között marad fenn.
 Lebegy állításának kulcsa magának a tömegnek a meghatározásában rejlik. Az elfogadott nézet szerint nincs különbség egy mozgó objektum tömege és egy gravitációs mező által az objektumra ruházott tömeg között. Más szavakkal az első, amit tehetetlen, vagy inerciális tömegnek is nevezünk, idézi elő, hogy egy autó eldeformálódik, ha egy másik járművel ütközik, míg az utóbbira, a gravitációs tömegre általában "súlyként" tekintünk. Ez az egyenlőségi szabály a tehetetlen és a gravitációs tömeg között igen nagy pontossági szinttel került megerősítésre. "Számításaim azonban azt mutatják, hogy egy bizonyos valószínűségen túl, van egy nagyon kicsi, ugyanakkor valós esély, hogy az egyenlet megbukik a gravitációs tömeg esetében" - mondta Lebegy.
Lebegy állításának kulcsa magának a tömegnek a meghatározásában rejlik. Az elfogadott nézet szerint nincs különbség egy mozgó objektum tömege és egy gravitációs mező által az objektumra ruházott tömeg között. Más szavakkal az első, amit tehetetlen, vagy inerciális tömegnek is nevezünk, idézi elő, hogy egy autó eldeformálódik, ha egy másik járművel ütközik, míg az utóbbira, a gravitációs tömegre általában "súlyként" tekintünk. Ez az egyenlőségi szabály a tehetetlen és a gravitációs tömeg között igen nagy pontossági szinttel került megerősítésre. "Számításaim azonban azt mutatják, hogy egy bizonyos valószínűségen túl, van egy nagyon kicsi, ugyanakkor valós esély, hogy az egyenlet megbukik a gravitációs tömeg esetében" - mondta Lebegy.
Ha valaki elég gyakran méri a kvantumobjektumok, mint például egy hidrogén atom súlyát, akkor bár az eredmény döntő többségében ugyanaz lesz, a mérések egy kis hányada eltérő eredményt mutat, megsértve az E=mc2 egyenletet. Ez jelentős fejtörést okoz a fizikusoknak, pedig a jelenség megmagyarázható lenne, ha a gravitációs tömeg nem egyenlő az tehetetlen tömeggel. "A legtöbb fizikus nem ért egyet ezzel, mivel szerintük a gravitációs tömeg pontosan megegyezik a tehetetlen tömeggel" - mondta Lebegy. "Az én véleményem azonban az, hogy a gravitációs tömeg nem lehet egyenlő a tehetetlen tömeggel az általános relativitás bizonyos kvantumhatásai miatt. Legjobb tudásom szerint ezt még senki sem vetette fel korábban"
Lebegy tavaly nyáron Stockholmban, egy kongresszuson ismertette számításait és azok következményeit, ahol a hallgatóságtól igen vegyes fogadtatásban részesült. Lebed megkérte tudóstársait, hogy értékeljék ki a számításait és felvázolt egy kísérletet is következtetéseinek tesztelésére. "A fizika legfontosabb problémája a mindenség elmélete - egy elmélet, ami minden természetben észlelt erőt leír" - taglalta Lebegy. "A fő probléma egy ilyen elmélethez való eljutásban a kvantummechanika és a gravitáció egyesítésében rejlik. Én megpróbálok kapcsolatot létrehozni a kvantumobjektumok és az általános relativitás között"
Lebegy érvelésének megértéséhez a gravitáció a kulcs. Papíron bebizonyította, hogy bár E=mc2 mindig igaznak bizonyul a tehetetlen tömeg esetében, nem mindig igaz a gravitációs tömegre. Einstein szerint a gravitáció a tér egy görbületének eredménye. Képzeljünk el egy szivacsmatracot, amin több tárgyat is elhelyezünk, mondjuk egy pingpong labdát, egy baseball labdát és egy tekegolyót. A pingpong labda nem fog látható bemélyedést létrehozni a matracon, a baseball labda is csak egy egészen parányit, míg a tekegolyó belesüpped a szivacsba. A csillagok és a bolygók ugyanígy viselkednek. Minél nagyobb egy objektum tömege, annál nagyobb mélyedést hoz létre a tér anyagában - más szavakkal, minél nagyobb a tömeg, annál nagyobb a gravitációs vonzás.
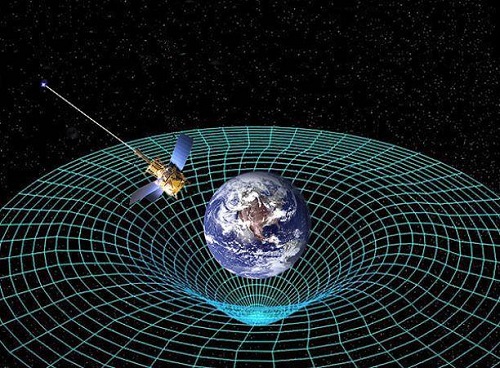
Ebben a modellben jól láthatjuk, hogy egy kis objektum, mint egy űrben vándorló aszteroida, könnyedén belekerülhet egy bolygó által létrehozott "mélyedésbe", ahol fogságba ejti a gravitációs mező. "A térnek van egy görbülete, és ha egy tömeget mozgatunk az térben, ez a görbület megzavarja ezt a mozgást" - mondta Lebegy, aki szerint a görbület különbözteti meg a gravitációs tömeget a tehetetlentől.
Elméletének tesztelését a legegyszerűbb kvantumobjektum, egy hidrogén atom súlyának mérésével kezdi. A hidrogén atom egy magból, egy protonból és egy magányos elektronból áll, ami a mag körül kering. Mivel várakozása szerint a hatás rendkívül kicsi lesz, rengeteg hidrogén atomra van szükség. Íme az elv: Egy ritka esetben az atommag körül keringő elektron egy magasabb energiaszintre ugrik, amire egy szélesebb pályaként tekinthetünk. Rövid időn belül az elektron visszaesik korábbi energiaszintjére. Az E=mc2 szerint a hidrogén tömege meg fog változni az energiaszintben bekövetkezett változással együtt.
Ez eddig szép és jó, de mi történik, ha ugyanezt az atomot elvisszük a Földről, egy olyan helyre, ahol a térnek nincs görbülete? Elméletileg ott az elektron már nem ugorhat át egy magasabb energiaszintre, mivel a lapos térben meg kell őriznie elsődleges energiaszintjét, vagyis ebben a közegben nincs ugrándozás. "Ebben az esetben az elektron csak a hidrogén atom első szintjét foglalhatja el" - magyarázta Lebegy. "Nincs rá hatással a gravitáció görbülete. Ezután közelebb hozzuk a Föld gravitációs mezőjéhez és a tér görbülete miatt már van esélye, hogy az elektron az elsőről a második szintre ugorjon, és a tömege különböző lesz"
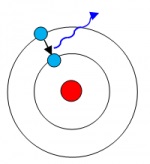 A földi energiaszinteken már mindenféle számítást elvégeztek, azonban Lebegy szerint ez nem sokat ér, mivel a görbület minden esetben ugyanaz, vagyis nincs perturbáció. Azonban azt eddig nem vették figyelembe, hogy az elektronnak azért van lehetősége a szintek közötti ugrálásra, mert a görbület megzavarja az atomot. "A súly közvetlen mérése helyett ezeket az energiaváltási eseményeket kellene észlelnünk, melyek foton kibocsátással adnak hírt magukról" - magyarázta.
A földi energiaszinteken már mindenféle számítást elvégeztek, azonban Lebegy szerint ez nem sokat ér, mivel a görbület minden esetben ugyanaz, vagyis nincs perturbáció. Azonban azt eddig nem vették figyelembe, hogy az elektronnak azért van lehetősége a szintek közötti ugrálásra, mert a görbület megzavarja az atomot. "A súly közvetlen mérése helyett ezeket az energiaváltási eseményeket kellene észlelnünk, melyek foton kibocsátással adnak hírt magukról" - magyarázta.
Magához a kísérlethez egy kis űrhajóra lenne szükség, amit egy hidrogéntartállyal és egy érzékeny fénydetektorral látnak el. A világűrben a tömeg és az energia közötti viszony megegyezik az atom számára, de csak azért, mert a lapos tér nem teszi lehetővé az elektron számára az energiaszint változást. "A Föld közelében a tér görbülete zavarja az atomot, ezáltal meg van az esélye az elektronnak az ugrásra, egy fotont bocsátva ki, amit rögzít a detektor" - mondta Lebegy, aki szerint az űrhajónak nem is kell túl messzire mennie. "A Föld sugarának két-háromszorosára kell küldenünk a szondát és működni fog a kísérlet"
Lebegy szerint munkája az első javaslat a kvantummechanika és Einstein gravitációs elméletének együttes tesztelésére a világűrben. "Nincsenek közvetlen tesztek a két elmélet összeházasítására. Ez nem csupán abból a szempontból fontos, hogy a gravitációs tömeg nem egyenlő a tehetetlenségi tömeggel, de azért is, mert sokan egyfajta rémként tekintenek erre a házasságra. Szeretném letesztelni és látni, hogy működik-e vagy sem" - összegzett.
Bár azóta a fizikusok számtalan kísérlettel és számítással igazolták Einstein egyenletét, és számos technológia, köztük a mobiltelefonok és a GPS navigáció is függ tőle, az Arizona Egyetem fizikus professzora, az orosz származású Andrej Lebegy nagy vihart kavart azzal a feltevésével, mely szerint az egyenlet nem minden körülmények között marad fenn.
 Lebegy állításának kulcsa magának a tömegnek a meghatározásában rejlik. Az elfogadott nézet szerint nincs különbség egy mozgó objektum tömege és egy gravitációs mező által az objektumra ruházott tömeg között. Más szavakkal az első, amit tehetetlen, vagy inerciális tömegnek is nevezünk, idézi elő, hogy egy autó eldeformálódik, ha egy másik járművel ütközik, míg az utóbbira, a gravitációs tömegre általában "súlyként" tekintünk. Ez az egyenlőségi szabály a tehetetlen és a gravitációs tömeg között igen nagy pontossági szinttel került megerősítésre. "Számításaim azonban azt mutatják, hogy egy bizonyos valószínűségen túl, van egy nagyon kicsi, ugyanakkor valós esély, hogy az egyenlet megbukik a gravitációs tömeg esetében" - mondta Lebegy.
Lebegy állításának kulcsa magának a tömegnek a meghatározásában rejlik. Az elfogadott nézet szerint nincs különbség egy mozgó objektum tömege és egy gravitációs mező által az objektumra ruházott tömeg között. Más szavakkal az első, amit tehetetlen, vagy inerciális tömegnek is nevezünk, idézi elő, hogy egy autó eldeformálódik, ha egy másik járművel ütközik, míg az utóbbira, a gravitációs tömegre általában "súlyként" tekintünk. Ez az egyenlőségi szabály a tehetetlen és a gravitációs tömeg között igen nagy pontossági szinttel került megerősítésre. "Számításaim azonban azt mutatják, hogy egy bizonyos valószínűségen túl, van egy nagyon kicsi, ugyanakkor valós esély, hogy az egyenlet megbukik a gravitációs tömeg esetében" - mondta Lebegy.Ha valaki elég gyakran méri a kvantumobjektumok, mint például egy hidrogén atom súlyát, akkor bár az eredmény döntő többségében ugyanaz lesz, a mérések egy kis hányada eltérő eredményt mutat, megsértve az E=mc2 egyenletet. Ez jelentős fejtörést okoz a fizikusoknak, pedig a jelenség megmagyarázható lenne, ha a gravitációs tömeg nem egyenlő az tehetetlen tömeggel. "A legtöbb fizikus nem ért egyet ezzel, mivel szerintük a gravitációs tömeg pontosan megegyezik a tehetetlen tömeggel" - mondta Lebegy. "Az én véleményem azonban az, hogy a gravitációs tömeg nem lehet egyenlő a tehetetlen tömeggel az általános relativitás bizonyos kvantumhatásai miatt. Legjobb tudásom szerint ezt még senki sem vetette fel korábban"
Lebegy tavaly nyáron Stockholmban, egy kongresszuson ismertette számításait és azok következményeit, ahol a hallgatóságtól igen vegyes fogadtatásban részesült. Lebed megkérte tudóstársait, hogy értékeljék ki a számításait és felvázolt egy kísérletet is következtetéseinek tesztelésére. "A fizika legfontosabb problémája a mindenség elmélete - egy elmélet, ami minden természetben észlelt erőt leír" - taglalta Lebegy. "A fő probléma egy ilyen elmélethez való eljutásban a kvantummechanika és a gravitáció egyesítésében rejlik. Én megpróbálok kapcsolatot létrehozni a kvantumobjektumok és az általános relativitás között"
Lebegy érvelésének megértéséhez a gravitáció a kulcs. Papíron bebizonyította, hogy bár E=mc2 mindig igaznak bizonyul a tehetetlen tömeg esetében, nem mindig igaz a gravitációs tömegre. Einstein szerint a gravitáció a tér egy görbületének eredménye. Képzeljünk el egy szivacsmatracot, amin több tárgyat is elhelyezünk, mondjuk egy pingpong labdát, egy baseball labdát és egy tekegolyót. A pingpong labda nem fog látható bemélyedést létrehozni a matracon, a baseball labda is csak egy egészen parányit, míg a tekegolyó belesüpped a szivacsba. A csillagok és a bolygók ugyanígy viselkednek. Minél nagyobb egy objektum tömege, annál nagyobb mélyedést hoz létre a tér anyagában - más szavakkal, minél nagyobb a tömeg, annál nagyobb a gravitációs vonzás.

Ebben a modellben jól láthatjuk, hogy egy kis objektum, mint egy űrben vándorló aszteroida, könnyedén belekerülhet egy bolygó által létrehozott "mélyedésbe", ahol fogságba ejti a gravitációs mező. "A térnek van egy görbülete, és ha egy tömeget mozgatunk az térben, ez a görbület megzavarja ezt a mozgást" - mondta Lebegy, aki szerint a görbület különbözteti meg a gravitációs tömeget a tehetetlentől.
Elméletének tesztelését a legegyszerűbb kvantumobjektum, egy hidrogén atom súlyának mérésével kezdi. A hidrogén atom egy magból, egy protonból és egy magányos elektronból áll, ami a mag körül kering. Mivel várakozása szerint a hatás rendkívül kicsi lesz, rengeteg hidrogén atomra van szükség. Íme az elv: Egy ritka esetben az atommag körül keringő elektron egy magasabb energiaszintre ugrik, amire egy szélesebb pályaként tekinthetünk. Rövid időn belül az elektron visszaesik korábbi energiaszintjére. Az E=mc2 szerint a hidrogén tömege meg fog változni az energiaszintben bekövetkezett változással együtt.
Ez eddig szép és jó, de mi történik, ha ugyanezt az atomot elvisszük a Földről, egy olyan helyre, ahol a térnek nincs görbülete? Elméletileg ott az elektron már nem ugorhat át egy magasabb energiaszintre, mivel a lapos térben meg kell őriznie elsődleges energiaszintjét, vagyis ebben a közegben nincs ugrándozás. "Ebben az esetben az elektron csak a hidrogén atom első szintjét foglalhatja el" - magyarázta Lebegy. "Nincs rá hatással a gravitáció görbülete. Ezután közelebb hozzuk a Föld gravitációs mezőjéhez és a tér görbülete miatt már van esélye, hogy az elektron az elsőről a második szintre ugorjon, és a tömege különböző lesz"
 A földi energiaszinteken már mindenféle számítást elvégeztek, azonban Lebegy szerint ez nem sokat ér, mivel a görbület minden esetben ugyanaz, vagyis nincs perturbáció. Azonban azt eddig nem vették figyelembe, hogy az elektronnak azért van lehetősége a szintek közötti ugrálásra, mert a görbület megzavarja az atomot. "A súly közvetlen mérése helyett ezeket az energiaváltási eseményeket kellene észlelnünk, melyek foton kibocsátással adnak hírt magukról" - magyarázta.
A földi energiaszinteken már mindenféle számítást elvégeztek, azonban Lebegy szerint ez nem sokat ér, mivel a görbület minden esetben ugyanaz, vagyis nincs perturbáció. Azonban azt eddig nem vették figyelembe, hogy az elektronnak azért van lehetősége a szintek közötti ugrálásra, mert a görbület megzavarja az atomot. "A súly közvetlen mérése helyett ezeket az energiaváltási eseményeket kellene észlelnünk, melyek foton kibocsátással adnak hírt magukról" - magyarázta.Magához a kísérlethez egy kis űrhajóra lenne szükség, amit egy hidrogéntartállyal és egy érzékeny fénydetektorral látnak el. A világűrben a tömeg és az energia közötti viszony megegyezik az atom számára, de csak azért, mert a lapos tér nem teszi lehetővé az elektron számára az energiaszint változást. "A Föld közelében a tér görbülete zavarja az atomot, ezáltal meg van az esélye az elektronnak az ugrásra, egy fotont bocsátva ki, amit rögzít a detektor" - mondta Lebegy, aki szerint az űrhajónak nem is kell túl messzire mennie. "A Föld sugarának két-háromszorosára kell küldenünk a szondát és működni fog a kísérlet"
Lebegy szerint munkája az első javaslat a kvantummechanika és Einstein gravitációs elméletének együttes tesztelésére a világűrben. "Nincsenek közvetlen tesztek a két elmélet összeházasítására. Ez nem csupán abból a szempontból fontos, hogy a gravitációs tömeg nem egyenlő a tehetetlenségi tömeggel, de azért is, mert sokan egyfajta rémként tekintenek erre a házasságra. Szeretném letesztelni és látni, hogy működik-e vagy sem" - összegzett.
 Nagyon jó sokat nevettem az utolsó mondatodon köszi..
Nagyon jó sokat nevettem az utolsó mondatodon köszi..