1406
Tényleg nem létezik?
-
 #1366
#1366
a relativitáselmélet értelmében a szabadon esés nem gyorsuló mozgás. ne, ne is fáradj a válaszzal, tudom, hogy nem vagy tisztában a relativitáslmélettel. -
Albertus #1365 Érdekeseket írsz.
http://forum.szkeptikus.hu/viewtopic.php?f=8&p=18341#p18341
Ezt már olvastad? -
Albertus #1364 "Nem szabad elfelejteni, hogy a relativitas pont az allitja, hogy a test szabadon es eromentesen mozog, amikor gravitacios mezoben 'esik'."
Valóban nem szabad elfelejteni.. Mert a folyamatosan gyorsuló mozgás (az esés) az bizony mozgásállapot változás.
Az erőhatás mentes állapotban viszont nincs mozgásállapot változás.
A relativitásnak ez a hamis állítása csak egy a sok közül. -
sublimiter #1363 Nem szabad elfelejteni, hogy a relativitas pont az allitja, hogy a test szabadon es eromentesen mozog, amikor gravitacios mezoben 'esik'.
A felvetesnek ugy van ertelme, hogy egy esni probalo testet folyamatosan megakadalyozzuk az esesben. /szep egy mondat lol/
Ekkor folyamatosan erot kell kifejteni, folyamatos a gyorsulas.
A kulonbseg annyi, hogy ebben az esetben a testet egy masikhoz kepest ugyan olyan potencialis energian tartod, mig sik teridoben noveled a gyorsitassal a mozgasi energiajat.
-
sublimiter #1362 "(gyorsulásnál a sebesség következtében idődilatációval számolhatunk? "
Nem teljesen egyenerteku a mozgo test idodilatacioja es a gravitacios 'terben' levoe.
Gondolj bele, a gyorsulasnal indulhatsz 0 sebessegrol. Ekkor nem lenne idodilatacio, majd az ido fuggvenyeben novekedne. Ennek a logikai szalnak igy nincs ertelme. -
lotsopa #1361 Amennyiben az állandó mértékü gyorsulást egyenértékünek vehetünk egy homogén gravitációs mezővel, (gyorsulásnál a sebesség következtében idődilatációval számolhatunk? gravitációs mezőben kimutatható [elméletileg] gravitonok, gravitációs hullámok jelenléte) akkor megkülönböztethetetlenek lennének, de a gyorsuló mozgást végző test energiája nő, a gravitációs mezőben levői viszont nem. (eltekintve attól amit annak a testnek az energiájából vesz el ami létrehozza a gravitációs mezőt) Ha a tömeg az energia egyik formája akkor nem tekinthető állandónak, de akkor mégsem ekvivalens a gyorsulás és a gravitáció? -
sublimiter #1360 A tehetetlensegi elv kimondja, hogy a tehetetlensegi es a gravitacios tomeg ugyan az.
http://hu.wikipedia.org/wiki/T%C3%B6meg#A_tehetetlens.C3.A9gi_.C3.A9s_a_gravit.C3.A1ci.C3.B3s_t.C3.B6meg_ekvivalenci.C3.A1ja
Ha a gravitacio egyfajta diszperzio mentes fenytores, akkor a tehetetlen tomeg is visszavezetheto egyfajta hullam-tulajdonsagra. Ha a hullamok racskent tudnak egymasra hatni, akkor az osszes tobbi ero felirhato erre a hatasmechanizmusra.
Ekkor minden anyaghullam racskent funkcional, es egy masik anyaghullam kepes megtorni ezen a racson. Ez valami olyasmi, mint a Bragg-diffrakcior, de a racs mozog, tehat jelen van a Doppler-eltolodas is.
A Bragg egyenlet es a Compton szoras egyenlete nagyon hasonlo. A hasonlosag nem veletlen.
Ha egy foton es egy elektron hat egymasra, akkor ennek a hatasnak az erossege a hullamhosszak kulonbsegetol fugg. Ez teljesen megfelel a Bragg-feltetelnek, ott is a hullamhossz es a d racstavolsag a fontos, ettol fugg a toresi szog.
A ket latszolag fuggetlen fizikai folyamat kozott szoros kapcsolat van.
Ez egy hipotezis, mert pontosan nem tudom kiszamolni.
De ha igaz, akkor ra lehet epiteni egy TOE-t.
Ha nem, akkor egy ujabb ertelmetlen szoveg kerult az amugy is ertelmetlensegekkel teleszort internetre.
xD
-
sublimiter #1359 Mielott barki nekikezdene a Schwarzschild megoldassal szamolni.
Nem annyi, hogy betesszuk a newtoni helyere, mert az alabbi harom sorban mindenhol a dt valojaban dT, vagyis a sajatido derivaltja, amit teljesen mashogy kell szamolni, mint a dt-t.
Sot az adott megoldas csak rs/2 egysegben szamolva ad helyes eredmenyt. Tehat mindent at kell skalazni erre, a fenysebessegtol kezdve az rs-ig bezarolag. -
sublimiter #1358 dpdp helyett a
do*do is r2-vel van szorozva -
sublimiter #1357 Igazabol ez sem ujdonsag annak, aki ismeri a Schwarzschild megoldast, hiszen az hasonlo.
ddr = -c*c*(r-rs)/(r*r*r)*dt*dt +(rs/2)/(r*(r-rs))*dr*dr +(r-rs)*do*do;
ddo = -dr*do*2/r;
ddt = -rs/(r*(r-rs)) * dt*dr;
A ddo {nalam ddp.y} szinte egy az egyben ugyan az. A ddt a sajatido es a koordinata-ido kulonbozosege miatt kell. A ddr {ddp.x}-nel a dpdp is r2-vel van szorozva, igy az en peldamban is jobb egyezes erheto el. Sot, a gyok(2) sem kell.
r2 = r-rs;
ddp.x = (-g*m/(r2*r)) + v*v*r2;
Ez az origo eltolas mar onmagaban kiadja az ellipszis-palya nagytengelyenek vandorlasat. A sajatido mar csak kis mertekben valtoztat ezen, nem az az ok, hanem az origo eltolodasa a Schwarzschild sugarra.
-
sublimiter #1356 http://en.wikipedia.org/wiki/File:Relativistic_precession.svg
http://en.wikipedia.org/wiki/Schwarzschild_geodesics
-
sublimiter #1355 Aki nem ismeri ez az egypont ketpont jelolest, annak talan ilyeszto is lehet. Pedig ismert dolgokat takatnak ezek. A hely elso derivaltja a sebesseg, a masodik a gyorsulas. A sebesseg a hely valtozasa, a gyorsulas pedig a hely valtozasanak valtozasa. Egyszeru.
A pontozast Newton talalta ki,
"Az első a Lagrange-féle jelölés, ő használta először a „derivált” kifejezést. A második a Leibniz-féle, ő differenciálhányadosnak nevezte (később Hamilton differenciálkoefficiensként említi). Newton a deriváltat ponttal jelölte: \scriptstyle{\dot{v}} és fluxiónak nevezte."
http://hu.wikipedia.org/wiki/Deriv%C3%A1lt
En d-vel jelolom ugyanezt. p a helyvektor, dp a sebesseg es ddp a gyorsulas.
r = p.x;
v = dp.y;
Itt addp.x az r..
ddp.x = (-g*m/(r2*r2)) + v*v*r;
Mig itt a szoggyorsulas van kifejezve
ddp.y = -2*dp.x*dp.y/r;
http://hu.wikipedia.org/wiki/Centrifug%C3%A1lis_er%C5%91
+ v*v*r
Mivel most polar-koordinatakkal szamolok, ezert itt v az a szogsebesseg.
-
sublimiter #1354 Amiket ir leirtam, azok kozul a legtobb alapszintu fizika /kellene hogy legyen/.
Ha a vilag olyan, ahogy en /es Lorentz vagy Schrodinger/ elkepzelem, akkor a TOE osszes reszletet mar az altalanos iskolaban oktatjak.
Ugy hivjak, hullamfizika.
-
Koppixer #1353 Na, akkor most nekikezdhetsz kidolgozni a TOE-t!
Vagy már eddig is abból közöltél részleteket?
-
sublimiter #1352 Mindezek ellenere valoszinu, hogy ez csak egy kozelites.
De a Schwarzschild radius 100 szorosaig egesz jo az egyezes az Einstein egyenletek Schwarzschild megoldasaval.
A fenytores is csak a helyes sajatidovel adhat jo eredmenyt. Az einsteini egyenletek ezt mar tartalmazzak, tehat azok biztos helyesek. Termeszetesen.
De a Lorentz-elv szerint is fel lehet irni a gravitaciot, meghozza fenytoressel.
Ennyi.
-
sublimiter #1351 Newtoni fizika cafolva?
Hat nem hinnem. -
sublimiter #1350 Kicsit visszaterve a newtoni gravitaciora. Az ember azt gondolna, ez lehetetlen, de polar-koordinatakkal biztos nem mukodik.
Semmi sem lehetetlen. A trukk az, hogy csak a gravitacios gyorsulasnal hasznalom a csokkentett r2 erteket. Nem irom ismet, hogy egyszeru, mert biztos bosszanto. xD
{
skalar r,r2,v,u;
vektor p3;
r = sqrtl(p.x*p.x + p.y*p.y);
u = atan(p.y/p.x);
dp.x = (p.x*dp.x + p.y*dp.y)/r;
dp.y = (p.x*dp.y - p.y*dp.x)/(r*r);
p.x = r;
p.y = u;
for(int j=0;j<lepes;j++)
{
p = p + dp*dt;
r = p.x;
v = dp.y;
r2 = r-rs*1.414;
// r2 = r;
ddp.x = (-g*m/(r2*r2)) + v*v*r;
ddp.y = -2*dp.x*dp.y/r;
ddp.z = 0;
dp = dp + ddp*dt;
p3.x = p.x*cos(p.y);
p3.y = p.x*sin(p.y);
p3.z = 0;
pont(p3*skala,0x00ff00);
}
}
http://en.wikipedia.org/wiki/Kepler's_laws_of_planetary_motion
-
sublimiter #1349 Ez pedig nem egy Einstein cafolat. Csak annyi a lenyeg, hogy az einsteini egyenletek egy fenytorest irnak le.
De ez minden szamolas nelkul is nyilvanvalo a Schwarzschild fenysebesseg egyenletbol.
A relativitas tokeletes.
Az mozgo orak lassulnak, a testek osszemennek. De nem igaz, hogy erre nincs magyarazat. Van.
Az egesz egyszeru hullamfizika. Schrodinger es Lorentz ezt tudta, de keptelenek voltak elmagyarazni. Nem csoda, hiszen meg ma is szinte lehetetlen.
Az egesz fizika rajuk epul. Talan el kellene hinni azt, amiben hittek.
-
sublimiter #1348 ds2 minden kordinata-rendszerben ugyan annyi. -
sublimiter #1347 Pontosabban a Minkowski metrikaban a ds2 az allado. A tavolsag negyzete minusz a fenyut negyzete. Ha ket esemeny kozott a tavolsag egyenlo a fenyuttal, akkor a ds2=0.
Ez a fenykup felulete.
-
palack #1346 v/c ami állandó. Mivel v-t nem tudjuk mérni (illetve értéke relativ más v-hez viszonyítva), ezért nem bizonyítható, hogy c állandó. Ez az ellentmondás úgy lett feloldva, hogy feltételezték, hogy s/t az állandó. Ez egy külső megfigyelő által vizsgált rendszerre (lézeresdi, M.M. kísérlet stb.) megfelelő, de mikor a megfigyelő a rendszer része (űrhajó, ikrek, stb.), már nem. Ez a tökéletes relativitás. -
sublimiter #1345 Mindig elrontom valahol. Helyesen:
c2y = gyok(c2 c2 - c2x c2x)
vagy
c1y = gyok(c1 c1 - c1x c1x)
-
sublimiter #1344 1.215947e-04
2.432175e-04
2.000232e+00
Lol, a kapott szog ketszerese a newtoninak, pedig csak a fenysebesseg kiszamolasahoz hasznaltam az egyik Schwarzschild egyenletet, mit nemreg linkeltem.
A progi a fenti egyenlettel szamolja a feny iranyvaltozasat, tehat fenytorest szammol.
dpx2 = dpx *c2*c2/(c1*c1);
Ennyi.
Vagyis nem egeszen. Tomeggel rendelkezo testre fenyszeru belso mozgasokat kell szamolni. Ez hazi feladat. Az eredmeny tobb, mint meglepo. Nem en fogom leirni a megoldast.
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
typedef long double skalar;
struct vektor
{
skalar x,y,z;
vektor() {x=0;y=0;z=0;};
vektor(int x_,int y_,int z_) {x=x_;y=y_;z=z_;};
vektor(skalar x_,skalar y_,skalar z_) {x=x_;y=y_;z=z_;};
vektor operator + (vektor v) {vektor v_;v_.x=x+v.x;v_.y=y+v.y;v_.z=z+v.z;return v_;};
vektor operator - (vektor v) {vektor v_;v_.x=x-v.x;v_.y=y-v.y;v_.z=z-v.z;return v_;};
vektor operator * (skalar s) {vektor v_;v_.x=x*s;v_.y=y*s;v_.z=z*s;return v_;};
vektor operator / (skalar s) {vektor v_;v_.x=x/s;v_.y=y/s;v_.z=z/s;return v_;};
};
skalar skalar_szorzat(vektor v1,vektor v2) { return (v1.x*v2.x + v1.y*v2.y + v1.z*v2.z);}
skalar hossz(vektor v1) {return sqrtl(skalar_szorzat(v1,v1));}
vektor normalt(vektor v1) { return (v1/hossz(v1));}
vektor vektor_szorzat(vektor va,vektor vb)
{
vektor v_;
v_.x=(va.y*vb.z)-(vb.y*va.z);
v_.y=(va.z*vb.x)-(vb.z*va.x);
v_.z=(va.x*vb.y)-(vb.x*va.y);
return v_;
};
skalar g,c,m,rs,dr,rx,ry,dt;
vektor p,dp,ddp;
int lepes;
void newton_gravity()
{
skalar r;
while(p.x<rx)
{
p = p + dp*dt ;
ddp = normalt(p);
r = hossz(p);
ddp = normalt(p)*(-g*m/(r*r));
dp = dp + ddp*dt;
p = p + ddp*dt*dt/2;
}
}
void refract_gravity()
{
skalar r,dpx,dpy,dpx2,dpy2,c1,c2;
vektor nx,ny;
while(p.x<rx)
{
r = hossz(p);
c1 = c*(1-g*m/(2*c*c*r)) / pow(1+g*m/(2*c*c*r),3.0);
p = p + dp*dt ;
r = hossz(p);
c2 = c*(1-g*m/(2*c*c*r)) / pow(1+g*m/(2*c*c*r),3.0);//uj fenysebesseg
ny = normalt(p);//beesesi meroleges
nx.x = ny.y;
nx.y = -ny.x;
nx.z = ny.z;
dpx = skalar_szorzat(nx,dp);
dpy = skalar_szorzat(ny,dp);
dpx2 = dpx *c2*c2/(c1*c1);
dpy2 = sqrtl(c2*c2 - dpx2*dpx2);
if(dpy<0) dpy2 = -dpy2;
dp = (nx*dpx2 + ny*dpy2);
}
}
void alapallapot()
{
g = (skalar)6.67428e-11;
c = (skalar)2.99792458e8;
m = (skalar)1.9891e30;
rs = (skalar)2*m*g/(c*c);
ry = 1392000e3;//sun R
rx = 150e9;
lepes = 2000000;
dt = (rx*2/c)/lepes;
p = vektor(-rx,ry,(skalar)0.0);
dp = vektor((skalar)c,(skalar)0.0,(skalar)0.0);
}
int main()
{
alapallapot();
newton_gravity();
skalar fi = -atanl((p.y-ry)/rx)*180/M_PI;
printf("%Le \n",fi);
alapallapot();
refract_gravity();
skalar fi2 = -atanl((p.y-ry)/rx)*180/M_PI;
printf("%Le \n",fi2);
printf("%Le \n",fi2/fi);
return 0;
}
-
sublimiter #1343 Oke, nezzuk a hazat.
Hogy mukodik a fenytores?
Mar megint matek, fuuu
sin(fi1)/sin(fi2) = c1/c2
sin(fi1)=c1x/c1
sin(fi2)=c2x/c2
(c1x/c1) / (c2x/c2) = c1/c2
c2 c1x /(c1 c2x) = c1/c2
c1x = c2x c1 c1/(c2 c2)
vagy
c1x c2 c2/(c1 c1) = c2x
c1y = gyok(c2 c2 - c1x c1x)
Mar csak egy fenysugar kell, ami elhalad a Nap mellett.
-
Saintgerman #1342 Hát ja. Ezzel a "furcsaságggal" nekem is szembekellett néznem, amikor azzal jöttem elő, hogy a gyíkemberek köztünk élnek...
Ezért írtam a szög-kalapács példát... ha az "építkezésben" egy részletre fókuszálsz, azt jobban láthatod mint a többi, de ne feledd: a cél az, hogy a "ház kész legen"... -
sublimiter #1341 Nezd, ahhoz, hogy eljussunk a naprendszer barmelyik bolygojara, eleg Newton egyenlete. Most akkor hibas?
Nem. Egy kozelites.
-
sublimiter #1340 Igy igaz.
-
sublimiter #1339 Igen, az a furcsa, hogy ez nekem magyarazat, nektek nem.
Peldaul a masik topikban a Feynman modszer egy egyszeru magyarazat arra, hogy miert megy a foton a legrovidebb uton.
Lathatoan nem erti ott senki, es emiatt agresszivek az emberek. En elmondanam, de az emberek jobb szeretnek harcolni az 'elveikert'. Valojaban csak duhosek, mert nem ertik.
-
steweee #1338 voltam itt pár hete, belemélyedtem a topicba és a szakirodalomba is. anélkül hogy nagyobb vitát robbantanék ki, pusztán közgazdászként gondolkodva felteszek egy kérdést, és kíváncsi vagyok az érvekre és ellenérvekre.
szóval mi van akkor, ha einstein tévedett a téridő-relativitás elmélettel ? ha az egész nem igaz, ahogy azt sokan támadják és legalább olyan hiteles tudományos cáfolatai vannak a dolognak mint úgymond "megérteni a paradoxont" ?
mi van akkor, ha arra a nagyszerű tudományos felfedezésre alapozva hogy megalkották az atombombát az ő elmélete alapján kész tényként kezelik a téridő görbületet meg hasonlókat is ? hiszen bebizonyosodott, hogy ő is tévedett több dologban amikben hitt, vagy amit tudományosan állított.
nem elképzelhető az, h ogy mivel a nyugat európai és egyesült államokbeli tudományos köröket szintén zsidók irányítják, így nem is szivesen ismernék el a tévedést, halogatják ameddig csak lehet, talán még egykét évtizedbe is beletelik míg tudományosan is lehet cáfolni és más elmélettel helyetetsíteni ? -
Albertus #1337 Az idő kvantumos típusú mennyiség. Mint ahogyan Planck E=h*f energia adagjai is kvantumos típusúak, de!
Nem keverendő össze a mérés-létrehozás-érzékelés kvantumossága, a lehetségesen felvehető állapotok folyamatosságának kizárásával.
Hogy jobban érthető legyen, vegyük Planck függvényét!
Igaz, hogy egy-egy konkrét f értékhez, csak egyetlen energia kvantum tartozik, de a felvehető frekvenciák sora folyamatos függvényű.
Azaz a fény kvantumossága egyben nem jelenti azt is, hogy csak adott kvantum sorozatok létezhetnének. Miután bármilyen frekvencia létezik, ezért bármilyen energiájú kvantum is létezik, f=0 --> f=infinity tartományban.
Az időre éppen így érvényes, miután az igaz, hogy az óráinkban egy-egy konkrét frekvenciájú órajelet alkalmazunk forrás időegységként,
ezért maga az időmérés típusa időkvantumokkal történik, de!
Miután tetszőleges frekvenciájú ( f=0 --> f=infinity tartományú) alap órajelet használhatunk, az időkvantumok nagysága nem korlátos.
Azaz tetszőlegesen kicsin infinitezimális időkvantumokat is használhatunk.
-
Saintgerman #1336 Jól elmagyarázod magadnak a dolgokat, de mondanál nekünk is valamit egyszerû halandóknak ezek a "cik - cak" ok nélkül, no meg a wiki nélkül is 
-
sublimiter #1335 Tovabba, ha vakuumban diszperzio lenne, akkor a tavoli csillagokrol erkezo feny kulonbozo spektrumban idobe el lenne tolva, mas palyaszakaszokat latnank.
Tudtommal ilyen nem tapasztalhato, tehat a vakuumban nincs diszperzio.
Magyarul a diszperzio teljesen rossz cafolat a gravitacio fenytoreses magyarazatara. -
sublimiter #1334 http://en.wikipedia.org/wiki/Uncertainty_principle -
sublimiter #1333 Ha az ido is kvantumos, akkor nem merhetsz egy adott idoegysegnel rovidebbet.
A Heisenberg-hatarozatlansag nem csak a
osszefuggesben ismert, hanem a-ben is.
http://upload.wikimedia.org/math/4/d/e/4dec67c5ef710e91f46619b9421804bb.png
Ez azt is jelenti, tobbek kozt, hogy egy adott energia-valtozast nem tortenhet egy adott idonel rovidebb ido alatt. Ilyen ertelemben az ido is kvantalt.
-
 #1332
#1332
O sem ertette h a "valosag" kontextualis.. 
-
 #1331
#1331
Tenyleg van(lehet) az idonek kvantuma..? -
sublimiter #1330 Egyszeru fenytoresnel csak a feny sebessege valtozik. Minden hullamhosszu fenynek ugyan akkora lesz a sebessege. Tehat ha nincs diszperzio, akkor minden szinu feny egy szogben torik.
Alap hullamfizika. -
sublimiter #1329 Egy latszolagfizikustol azt hallottam, hogy a gravitacio nem lehet fenytores, mert ott a hullamhossztol fugg a toresi szog.
Mondom magamban, uristen. Es ez fizikus.
Akkor lassuk.
http://hu.wikipedia.org/wiki/F%C3%A9nyt%C3%B6r%C3%A9s
ha L1=20 es L2=10 az ugyanakkora toresi szoget ad, mint L1=10 L2=5.
Tudni kellene szamolni. Ekkor minden hullamhosszu feny ugyanolyan sebesseggel terjed. Ez tortenik a vakuumban.
A prizman a feher feny szivarvanyszeru szetszorodasanak nem ez az oka, hanem a diszperzio.
http://hu.wikipedia.org/wiki/Diszperzi%C3%B3
De ellenorizheto ez maskepp is.
Ki nem erti a fizikat,
LOL
Tehat a gravitacio lehet fenytores, mert ott csak a sebesseg valtozasatol fugg a toresi szog, nem ugy, mint a diszperzioval megbonyolitott esetben.
A gravitalo tomeg fele egyre jobban lassul a feny.
http://en.wikipedia.org/wiki/Schwarzschild_metric
Ennyire egyszeru.
-
sublimiter #1328 Nem latom ertelmet, tobb okbol.
Eloszor is matekkal felirhato egy megfigyelt folyamat. A feltamadast tudtommal meg nem latott senki, habar a bibliaban volt valami utalas ra, de ebbol egyenletet felirni....
Masodszor, milyen tulajdonsagai vannak a 'feltamadasnak', amit szamokkal le lehet irni? -
#1327 TC.sublimiter.
Írd le légyolykedves a feltámadást matematikai képletekben!!!!!!





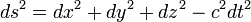

 -ben is.
-ben is.


