84
-
zizikus #84 Udvozletem!
Hat csak annyit fuznek hozza a kommentjeimhez, hogy elvileg jok, csak a kepleteket felejtettem el. :-) Regen volt mar.... :-) Pontosabban az omega-t, meg a centripetalis gyorsulast. Elnezest kerek erte!
-
Archenemy #83 Tőled meg elég lett volna annyi, hogy "mire írtad ezt?". -
Vol Jin #82 "omega =43 000 /60 = 717 1/s
a=omega^2 x r (r=10 000m)
a=514089 * 10^4 m/s^2
a=5.14089 * 10^9 m/s^2
Azaz kb. 5 milliard m/s^2, ami sok, de szemben a gravitacios 4000 milliardjahoz, meg mindig keves."
Majdnem jó. Annyi a különbség, hogy az omega az 2PI-szer nagyobb, mint a frekvencia. :-) Merhogy szegény, nem a fordulatszámot, hanem a szögsebességet jelenti radiánban. Tehát nem azt, hogy hányat forog szegény, hanem azt, hogy hány fokot másodpercenként, és természetesen nem fokban, hanem radiánban.
Úgyhogy 20 milliárd g-re jön az ki. -
Vol Jin #81 "A G pedig nem gyorsulast jelol, hanem a gammat, ami bizony univerzalis allado."
Nem mondtam, hogy az a G a jól ismert 9,81 m/s2. Egy olyan érték, ami a Földre jellemző. Mint a c a légellenállásnál. A trabantnak is van egy, meg egy ferrarinak, és a két érték tök más, mert más a trabant és a ferrari alakja. Jelen esetben más a Föld és egy neutroncsillag tömegeloszlása. -
zizikus #80 Ha mar belejottunk:
A Nap tomege
1.98892 * 10^30 kg
A Neutroncillag tomeget vegyuk 2 naptomegnek.
Mn=3.977784 * 10 ^30kg
g=G*(m1/r^2)
G=6.67 * 10^-11
r=20 000/2=10 000m
Ha igy szamolunk akkor 26* 10^11 m/s^2 jon ki. Ez 2600 milliard m/s^2. Azaz, ha a foldi 10 m/s^2 el akarjuk kifejezni, akkor 260 milliardszor akkora mint a Foldon.
Az elterest a korabbi szamolasomhoz a tomeg megsaccolasabol adodott.
Persze elszamolhattam ezt is.
Zizikus
-
zizikus #79 Udvozletem ismet!
Csak meg egy link:
Neutron Csillag
Az idevago resz:
Egy tipikus neutroncsillag felszínén tapasztalható gravitációs mező megközelítően 2x1011-szer erősebb, mint a Föld felszínén. Ennek megfelelően a szökési sebesség elérheti a 100 000 km/s értéket, azaz a fénysebesség egyharmadát. A mező ereje gravitációs lencsehatást okoz, mely a csillag saját fényét is eltéríti. Ez azt a hatást okozza, hogy a csillag felszínének több mint a fele látható, bármely irányból is figyeljük meg azt.[3]
Itt azt irja, hogy 2*10^11 szer akkora mint a Foldon. Azaz 200 milliardszor akkora. A Foldon kb. 10, akkor ez 2000 milliard m/s^2.
En 4000 milliardot kaptam. Nagysagrendi becslesnek nem rossz. Az idezett cikkben a Neutron csilagog tomege 1,94 és 2,74 naptömeg. A szamolasombol, illetve a cikkben szereplo elterest okozhatja a tomeg illetve az atmero elterese.
Zizikus
-
zizikus #78 Udvozletem mindenkinek!
Mint Vol Jin ramutatott, az elso hozzaszolasomban tenyleg rosszul adtam meg egy kepletet. A helyes:
acp=omega^2*r
igy a fentieket figyelembeveve:
omega =43 000 /60 = 717 1/s
a=omega^2 x r (r=10 000m)
a=514089 * 10^4 m/s^2
a=5.14089 * 10^9 m/s^2
Azaz kb. 5 milliard m/s^2, ami sok, de szemben a gravitacios 4000 milliardjahoz, meg mindig keves.
Kerek mindenkit, ezt vegye figyelembe! Koszonom!
Úgyhogy a "g=G*(m1/r^2)" képlet értelmetlen, illetve nem univerzális, csak a Földre vonatkozik, és csak azért lett létrehozva, mert valaki akart egy képletet, és legyártott egyet, amiben a G nem egy univerzumra érvényes állandó, hanem csak a Földre, éppen ezért minek.
Szerintem mukodik. A gravitacios torveny mukdik a Foldon is (itt sem pontszeru a test, valamint nem homogen tomegeloszlasu a Fold-sem.) A gravitacios torveny fenti eredmenye eppen az integralok osszege. A G pedig nem gyorsulast jelol, hanem a gammat, ami bizony univerzalis allado. A Fenti kepletben a Fold tomege van megadva (m1) es a sugar (r), semmi mas nem utal a Foldre. Ide lehetne a Hold tomeget es sugarat is beirni, azzal meg is kapnank a Holdon merheto nehezsegi gyorsulas erteket (persze meg kell meg hatarozni a forgasbol szarmazo eroket is).
Gravitacio
Idezet a cikkbol:
Szigorúan véve ez a törvény csak pontszerű objektumokra vonatkozik. Ha a tárgynak térbeli kiterjedése van, az erőt integrálszámítással kell megadni. Kimutatható, hogy ha a tárgy gömbszimmetrikus tömegeloszlású, akkor az integrálszámítás ugyanazt az eredményt adja, mintha a test pontszerű lenne. A tárgytól távolodva a kiterjedt valódi és a pontszerű elméleti tömeg közötti elvi különbség egyébként is egyre kisebb jelentőségűvé válik.
Ez pontosan azt jelenti, hogy ha a nem pontszeru testrol van szo, de a kulonbozo surusegu retegek egymasra epulnek, akkor siman hasznalhato a fenti keplet. Akkor kell Integrallal szamolni, ha a tomeg (suruseg) nem hejas szerkezetben valtozik. Ha a suruseg a melyseggel linearisan valtozik, akkor ugyan ez lesz az integralok erteke a felszinre vonatkoztatva. Ugyan ezt kapjuk, ha hagyma modjara epulnek fel a kulonbozo surusegu retegek.
Zizikus
-
Vol Jin #77 200 milliárd g a gravitációs erőhatás egy 20 km átmérőjű neutroncsillag felszínén. A "g=G*(m1/r^2)" képlet meg azért mehet a kukába, mert a neutroncsillag nem a Föld. Itt a G érték a Földre vonatkozik. Mert valójában a Föld minden pontja vonz minket. Ami messzebb van, az gyengébben, ami sűrűbb, az meg erősebben. Itt a nagy G a Föld eltérő sűrűségű és rétegeinek és a felszíntől való távolságainak integrálásával kihozható érték lenne. Ráadásul a szögfüggvények is befigyelnének, mert minket Moszkva is vonz, aminek ellenpontja Marokkó, ami szintén vonz minket, amik oldalirányban kioltják egymást, de mivel a felszín görbe, nekik is van a bolygó közepe felé ható vonzása ránk nézve.
Úgyhogy ez az egész képlet nem használható egy neutroncsillagra űgy, hogy a G marad, csak a sugár meg a tömeg más. Van fogalmunk nekünk arról, hogy milyen sűrűség eloszlás van egy neutroncsillagban. Pár csillagásznak van erre elmélete, a feltételezett adatokat benyomták egy modellező számítógépbe, az meg gondolom méteres kockákra bontotta a neutroncsillagot, és lemodellezte. Kijött 200 milliárd g egy átlagosra. De az is lehet, hogy valami közvetett úton egy megfigyelt lencsehatásból számítottak. Nem tudom, nem vagyok csillagász.
A centripetális hatás meg az a = r x omeganégyzet képlettel 20 milliárd g.
Egyébként a rád ható gravitációs hatás zömét a talpad alatti 100 km-es tömb adja. Mert ami egy km-el a talpad alatt van, az százmilliószor erősebben vonz, mint a Föld túloldalán lévő pekingi utcakő. Mivel az tízezerszeresen is messzebb van. Sőt még annál is messzebb, és mivel négyzetesen csökken a hatás a távolsággal, kijön a százmilliósnál is nagyobb nagyságrendi különbség.
Egy égitest felszínén a gravitáció nem pontszerű testek modelje alapján számítható, hanem integrálszámítással, amiben tényező a távolság mellett a sűrűségeloszlás is.
Úgyhogy a "g=G*(m1/r^2)" képlet értelmetlen, illetve nem univerzális, csak a Földre vonatkozik, és csak azért lett létrehozva, mert valaki akart egy képletet, és legyártott egyet, amiben a G nem egy univerzumra érvényes állandó, hanem csak a Földre, éppen ezért minek. -
zizikus #76 Tiszteletem!
Arra probaltam ravilagitani az akkori hozzaszolasomban, hogy mekkora lehet valojaban a gravitacios tererosseg a neutron csillag felszinen. Erre azert gondoltam, mert tobben felteteleztek, hogy a forgasbol szarmazo, ellentetes iranyu terfogati ero es a gravitacios ero kozel azonos nagysagu lehet ott. Arra a tevutra is ratevedtek tobben korabban, hogy a felszinen merheto nehezsegi gyorsulas nem tartalmazza a forgasbol szarmazo erohatast.
A tenyleges ertek megsaccolasahoz kellett egy szamszeru ertek a kepletbe, mivel nem tudtam milyen tomegu a neutron csillag. Szerencsemre a cikkben szerepel, hogy kb. 1 000 000 Fold tomegenek felel meg, a Wikis cikkben pedig epp a Fold tomege van megadva.
A masodik nagyobb hozzaszolasomban eppen Onnek is uzentem burkolva kicsit:
50,. hozzaszolasban irta:
Merthogy a két erőt kivonni kell egymásból, tehát amikor a két erő ellentétes irányú, akkor az általános iskola alsó tagozatos matekanyaga jusson eszedbe, hogy a negatív szám kivonása az olyan, mintha a pozitív értékét adnád hozzá a másikhoz. Ezért mondom, hogy a két erőt összeadni kell, mert ellentétes irányúak.
A testre hato eredok kiszamitasanal az eroket osszeadni kell, de vektorialisan. Fossz=F1+F2+F3+....+Fn A fentebb irtak ennek nem tesz eleget.
Erre reagaltam a kocsikerekes es a muholdas hasonlattal.
Mint korabban irtam, nem szamoltam utana a kepletekben leirtaknak, csk fejben, de szerintem nagysagrendileg jok.
Zizikus
-
physis #75 Ez akkor gondolom nem más, mint az árapályhatás, csak persze olyan kicsiny objektumok esetén mint az ember, viccesnek hangzik így mondani, de valójában erről van szó. A hírhedt spagetti-hatás, ami a feketelyuk vagy a neutroncsillag közelébe eső ember halálát okozza, az valójában árapályhatás. Úgy tudom a feketelyukba eső ember halálát nem is valami rejtélyes hatás okozza, sőt, az eseményhorizontnak sincs sok köze hozzá. A feketelyuk vagy a neutroncsillag felé eső ember egyszerűen a hétköznap, jólismert árapályjelenségbe hal bele, csak persze ez itt egész kisméretű testek esetében is kézzelfogható. A halál akkor következik be, amikor az árapályerők elérik azt a mértéket, amit a test szakítószilárdsága már nem bír. Ez bekövetkezik persze neutroncsilagnál is, feketelyuk esetében pedig egyaránt bekövetkezhet az eseményhorizonton kívül és belül is, a feketelyuk méretétől függően: kicsiny feketelyukaknál még ,,időben'' érezhető a fájdalom, viszont óriás feketelyuknál a fájdalom -- alattomos módon -- már csak jóval az eseményhorizont átlépése után jelentkezik (amikor már késő), Elméletileg magát az eseményhorizontot az ,,öngyilkos'' megfigyelő észre sem veszi átlépés közben, a testében létrejövő stressz a gradienstől függ, ami persze egyre közelebb egyre nagyobb lesz. -
physis #74 Szerintem értékes volt ez a feladat, én az ilyeneket értékesnek tartom, ezek ürügyén belső képeket lehet megmozgatni és ütköztetni, amik ott lenn lapulnak a mélyen az emberi képzetben, nem is teljesen tudatosan. Állítólag minden embernek van egy fizikai világképe, tudatosan vagy tudattalanul, még a kisebb gyereknek is. A gyerekek kb. az arisztotelészi fizikának megfelelő belső képzetekkel indulnak, és ez jó esetben továbbfejlődik, de nem magától (a nem-mérnök felnőttek a hétköznapi életben többnyire megtartják az arisztotelészi fizikát), hanem a tudatos fizikatanulás során. Az oktatásban az a nehézség van, hogy a képleteket úgy is meg tudja tanulni az ember, hogy a belső fizikai világát valójában érintetlenül megtartja, és a képletet csak zárványszerűen teszi magáévá. A belső képeket nehéz igazából elérni, ezért jók szerintem az ilyen feladatok, amik rákényszerítik az embert a belső képek ütköztetésére. -
pasi29uk #73 A neutron csillagok forgási sebessége akár 43.000 rpm is lehet a cikk szerint. De ez magnetár típus így csak picivel többet mint 8 rpm. Lassul, mert belecsapodott valami nagy...
"A neutron csillag a fekete lyukhoz legközelebb álló közvetlenül észlelhető objektum"
jelentős szerepet játsz6ott ebben. szvsz -
Vol Jin #72 De hogy jön a Föld tömege egy neutroncsillaghoz? -
Vol Jin #71 Erre már én is rájöttem. Viszont pontszerűen gondolkodunk, ami itt nem igaz, mert ahol 20 milliárd g-erőről van szó, ott az ember magassága, és a 10 km sugár összemérhető, még ha tizedszázalékos mértékben is. De a tizedszázalék is itt már milliónyi g-erő. -
Vol Jin #70 Tök igazad van. Csak neked volt időd átgondolni, én megf balga módon nyomtam elsőre azt, amit fejben levezettem. Mentségemre legyen mondva, hogy igen extrém szituációról van szó, ahol nem elégséges a fizika tananyag ismerete, hanem kombinálni is kell. :-) -
Vol Jin #69 Már én is rájöttem. :-D
Physy fogalmazta meg jól, hogy van felületi és van térfogati erő. Itt valóban mindkét erő a test mindkét részecskéjére hat, tehát kiegyenlítődik, és nem a rakétás eset áll fent, ahol a pilóta segge nyomja az űlést, és a részecskék egymásnak adják át az erőhatást.
Viszont van egy csavar, amire senki nem számított. Mivel a sugár 10 000 méter, ami egy ember magasságának 6000-szerese, a talp és a fej között nem egészen pontszerű a távolság. Tehát, ha 20 milliárd g-ről van szó a g különbség milliós nagyságrendű. Ha mondjuk a felszínen a talpnál kiegyenlítődne is a g, a fejtetőnél milliós g különbség lenne, ami azért igen komoly. A felszíni gravitáció is eltérő lenne akár méteres távolságokon is. Szóval komoly bukdácsolások, szétszakadások, pörgések lennének. -
duke #68 " Ellentétesen ható térfogati erők (ellentétben a felületi erőkkel),,fájdalommentesen'' semlegesítik egymást, nincs tépő-húzó-nyomó-nyíróhatás, nincs mechanikai stressz."
Na igen ez terfogati ero hianyzott nekem, probaltam rugoval, gumikotelel modellezni, de ugy nem allt ossze a kep. -
Drinkman #67 Ott a pont én is gecibuta vagyok! 
De attól még Vol Jin te is az vagy mert következetesen hülyeséget beszélsz és még meg is magyarázod!
-
physis #66 Köszönöm, én is üdvözlöm a fórumon. Az #56-ban írt számításnak (kapcsolva alul) is örülük, nem ellenőriztem, de szerintem jól összevág azzal, miért is maradhatnak szinte tökéletes gömb alakúak a neutroncsillagok (úgy tudom, gömbhöz való pontosságuk az ember által eddig alkotott legestökéletesebb gömbökkel, azokkal a fucsa szilíciumgöbökkel van kb. egy szinten). -
zizikus #65 Udvozlet!
A 63. hozzaszolas nagyon szemleletes!
Zizikus -
physis #64 Ugyanakkor ezt a szemléleti képet váltogatom a másik szemléleti képpel is, amely inkább a forgómozgás dinamikai feltételére hivatkozunk
a_cp növelése változatlan F_g mellett F_s csökkenését vonja maga után, hiszen a forgómozgás dinamikai feltétele csak így állhat fönn továbbra is.
-
physis #63 Szerintem használható a lift-analógia, az analízis figyelmebevételével, hogy érezzük, hol egyszerűsítünk, hol ,,rövidítünk'' le valamit.
Az én szemléleti modellemben lefelé ,,gyorsul a lift'', mert a bolygófelszín a görbülete miatt folyamatosan ,,kihajlik'' a test ,,alól'':
(képforrás: Wikimedia Commons)
A Föld esetében is észrevehető a lehajlás, pár kilométertávon nézve néhány decimétert ,,hajlik le'' a földfelszín. A forgó földfelszín tehát folyamatosan ,,lehajol'', kihajlik'' alólunk.
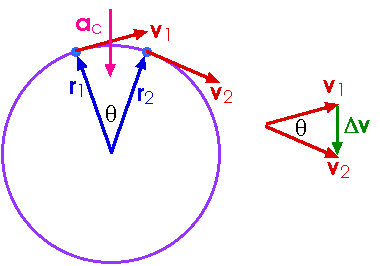
Ha csekély Δθ szögelfordulás mellett megrajzolom a test sebességvektorának változását, lefelé mutató Δv vektorkülönbözet jön ki:
(képforrás innen). Ennek megfelelően a centripetális gyorsulás vektora is ,,lefelé'' mutat, ez megfelel a fenti ,,lefelé gyorsuló liftes'' szemléleti analógiának.
A térfogati erők (ilyen a gravitációs erő és mindenfajta virtuális erő, mármint ha nem inerciarendszerben dolgozik az ember) nem hoznak létre fájdalmas harapófogó-hatást, mert a test minden egyes atomjára hatnak (ezek tehát nem felületi erők). Ellentétesen ható térfogati erők (ellentétben a felületi erőkkel),,fájdalommentesen'' semlegesítik egymást, nincs tépő-húzó-nyomó-nyíróhatás, nincs mechanikai stressz. -
duke #62 Annyiban javitan magam, hogy a liftes meg a repulos pelda onmagaban nem teves, csak nem alkalmazhatok gravitacio kontra centrigualis ero esetre. -
zizikus #61 Udvozletem!
"Csak gondold végig, hogy egy egy g-vel felfelé gyorsuló szerkezettel mekkora erő hatna a pilótára. Pont kettő g. Hidd el nem súlytalannak érezné magát."
"Könnyen ellenőrizheted egy liftben. Ha elindul fölfele a lift, nagyobb súly fog nehezedni a lábadra, amíg gyorsul."
Ez igy van, de ez a gyorsulas kicsit maskeppen van, mint a centripetalis. A ketto kozott a legnagyobb kulonbseg, hogy az egyik a sebessegvektor nagysagat valtoztatja, a masik pedig "csak" az iranyat valtoztatja meg.
Ha a ket erot ezesetben osszeadnank, akkor azt kellene felteteleznunk, hogy peldaul egy auto kerekere tapadt sar annal jobban tapadna a kerekhez, minel gyorsabban forog. Nem ez tortenik. A Gravitacios terben a testre a tomegkozeppont fele mutato sugariranyu ero hat. A forgasbol szarmazo ero pedig a forgas kozeppontjabol sugariranyban kifele hat. (Ezert adott sebessegnel lerepul a sar a kocsikerekrol) Igy az eredo ero a gravitacios- a centri. Maskeppen hogy keringhetnek pl. stacionaris palyan muholdak? Ott nincs alatamasztas sehol sem.
Az alatamasztas ott jon be a kepbe, hogy a tomegpotra hato erok eredoje 0 , mert a felszinhez viszonyitva nem gyorsul. A gravitacios-forgas miatt fellepo erokulonbsegeket kell a feluletnek allnia, ez lesz a test sulya, ekkora erovel nyomja a talajt.
Zizikus
-
duke #60 "Csak gondold végig, hogy egy egy g-vel felfelé gyorsuló szerkezettel mekkora erő hatna a pilótára. Pont kettő g. Hidd el nem súlytalannak érezné magát."
"Könnyen ellenőrizheted egy liftben. Ha elindul fölfele a lift, nagyobb súly fog nehezedni a lábadra, amíg gyorsul."
Ez igy biztos hogy teves, de azert egy kisse elbizonytalanitott, es nem is tudom most ertelmezni a kulonbseget, ezen el kell gondolkodnom. De mas az, hogy egy repulo, vagy lift alulrol emel, mint az hogy az ugynevezett fiktiv centrifugalis ero huz. Mellesleg a beidezett wikipedia oldalon is azt irjak amit mondtam.
"egyrészt a Föld forgása miatt nemcsak a tömegvonzás, hanem centrifugális erő is hat a tárgyakra, mely a gravitáció ellen hat," -
zizikus #59 "m1=5.97 *10^24 * 1 000 000 (cikkben benne van)"
Ez hol van benne?
A Fold tomege a Wikis linkbol kiderul, valamint azt tudtam fejbol is. A cikkben pedig az van irva, hogy a Fold tomegenel 1 millioszoros tomeg koncentralodik 20 km atmeroju terreszbe.
Zizikus -
Vol Jin #58 "m1=5.97 *10^24 * 1 000 000 (cikkben benne van)"
Ez hol van benne? -
Vol Jin #57 Egyél, hugyozzál, szarj és bassz, valamit nyomasd a kedvenc FPS-ed! -
zizikus #56 Udvozletem!
Nem ertem, mennyit szamoltak, es hogy jott ki mindez. Hol 1/min, hol atmero a kepletekbe, nem igazodom ki rendesen, elnezest.
A nehezsegi gyorsulas tartalmazza a forgasbol szarmazo erok altal okozott gyorsulasokat is, raadasul vektoros formaban.
Nehezsegi gyorsulas
Kiszamolgattam mekkora a szimplan a gravitacios gyorsulas allo helyzetben:
g=G*(m1/r^2)
G=6.67 * 10^-11
m1=5.97 *10^24 * 1 000 000 (cikkben benne van)
r=20 000/2=10 000 (cikkben benne van)
Nekem korulbelul 4000 milliard m/(s^2) jott ki.
Forgas miatt:
omega =43 000 /60 = 717 1/s
a=omega x r (r=10 000m)
a=7.71710^6
Namost, 4000 milliard minusz 7 millio, az marad 4000 milliard. ez kb 400 milliard szorosa a foldi erteknek.
Ha nem ekkora lenne, akkor nem is lehetne neutron a felszine. 10 g nem eleg abben a fazisban tartani az anyagot.
Kerem ellenorizzek a szamolasomat, mert csak kutyafuttaban volt ra idom.
Zizikus
-
mester1987 #55 A #22 hsz-t meg konkrétizálom ilyenek kedvéért, mint te:
Szóval a színvonal, hogy minden ilyen cikknél elkezd menni a farokméregetés, ki mennyire okos és ki mennyire tud okoskodni és ki mennyire tudja a másikat felhúzni.
Na ez az SG színvonal, így nélkülem is jól megvannak akik szeretik ezt csinálni. Tény, hogy nem mindenki! -
mester1987 #54 Akkor ne kérdezz. -
physis #53 Ábra link -
physis #52 A galériámban normálisan látszik a kép, ide valahogy használhatatlanul ilesztődik be -
physis #51 Az eredeti csillagászati kontextustól eltekintve most, nekem tetszett ez a kompetenciapélda. Elégedetlen vagyok a szemléleti képemmel ezért kedvelem az ilyeneket. Sokszor elrontom, néha összejön.
A lényeg itt szerintem az, hogy a liftanalógiában a helyes analógia az, hogy ,,lefelé indul a lift'', nem le.
Persze ez csak érzés volt, ezért megpróbáltam végignézni az erőket. Az erő valójában egy viszony két test közt, ezt színezéssel próbálom kiemelni az ábrán (a színezés a hatást kiváltó test szerint megy, nem az elszenvedő test szerint).
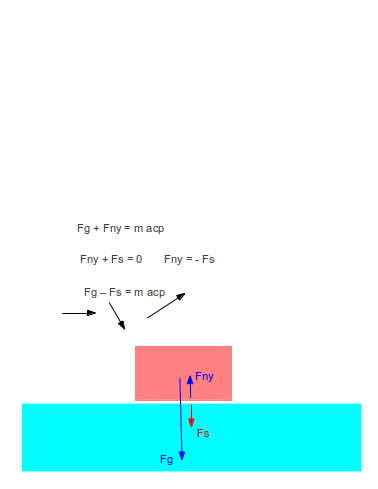
A testre Fg gravitációs erőt fejt ki a bolygó (F_g gravitációs erő, ennek ellenereje a bolygó középpontjában ,,hat'' a test részéről a bolygóra, de ez most nem fontos).
A testre még a bolygó felszíne is fejt ki erőt (Fny nyomóerő).
A testre ható erők eredője tehát Fg + Fny (ahol persze Fny ellentétes irányú vektor). Ennek az eredő erőre kell teljesülnie a körmozgás dinamikai feltételének: körmozgást végző testre ható erők eredője = centripetális gyorsulás és tömeg szorzata.
F_g + F_ny = m * a_cp
A súlyerő: amivel a test nyomja az alátámasztást. Ezt a test fejti ki az alátámasztásra, ezt tkp. nem más, mint az előbb Fny-nyel jelölt nyomóerő ellenereje (az ellentétes színezéssel ezt próbáltam kiemeleni).
F_s = - F_ny
A két képletből együtt következik:
F_g - F_s = m a_cp
A példában elképzelt helyzet: megnő a centripetális gyorsulás (ezt a felfelé bukó ferde nyíllal jelöltem az a_cp betűjel alatt). A többi mennyiségnél is bukó nyilakkal próbáltam jelölni a legalsó képlet alatt, melyik mennyiség nő, melyik csökken csökken. Szóval onnan indulunk ki, hogy az a_cp centripetális gyorsulás nő, tehát az m * a_cp is nő. Ezt kell ,,kigazdálkodni'' a testre ható egyes erőknek. Mivel F_g változatlan marad (a tömegvonzás változatlan), ezért szükségszerűen az F_s súlyerőnek kell csökkennie. Egy felpörgő bolygó egyenlítőjén valóban csökken a súlyerő (ez a Földnél is megfigyelhető gondolom). A sarkon (pólusokon) álló testeknek a felszínre kifejtett súlyerejét persze nem csökkenti ez a hatás. -
Vol Jin #50 Aha, akkor ellenőrizd már le, hogy mit buktál be. Csak gondold végig, hogy egy egy g-vel felfelé gyorsuló szerkezettel mekkora erő hatna a pilótára. Pont kettő g. Hidd el nem súlytalannak érezné magát.
És akkor azt is gondold végig, hogy miként nézted be, hogy osztottál egy másik számításodnál.
És akkor azt is gondold végig, hogy miért akkor érzed magad súlytalannak, amikor zuhansz. Nem akkor egyenlítődik ki a két erőhatás, amikor emelkedsz, hanem akkor, amikor zuhansz. Merthogy a két erőt kivonni kell egymásból, tehát amikor a két erő ellentétes irányú, akkor az általános iskola alsó tagozatos matekanyaga jusson eszedbe, hogy a negatív szám kivonása az olyan, mintha a pozitív értékét adnád hozzá a másikhoz. Ezért mondom, hogy a két erőt összeadni kell, mert ellentétes irányúak.
Ha még kivontál volna, akkor azt mondom egyszerűen elbóbiskoltál. De te osztottad a 200 milliárdot a 20 milliárddal, és kihoztad, hogy az 10 g.
Na most gondold végig ezt a gecibuta vagy fotót. -
Vol Jin #49 "Ha visszaellenőrzöd rájössz hogy 716-al számolgattam."
Az EPM-et néztem be Hz-nek. Azzal tényleg 20 milliárd g hozzávetőleg. A gravitáció viszont 200 milliárd. Tehát a gravitáció még mindig 10xszer nagyobb. Ebből viszont te 10g-t számoltál, ami a testre hat. Ez alapvető tévedés, mert osztottál, amikor összeadni kellett volna. A valóságban 220 milliárd g erő hatna a testre. Mármint ekkora erő nyomná össze. A gravitáció húzná lefele, a perdület tehetetlensége meg hajigálná felfele, azaz a két erő összege nyomná össze. -
Vol Jin #48 "Ha az elképzelésem helyes akkor lényegében a protonok és az elektronok gyakorlatilag egymásba préselődnek és neutron lesz belőlük? Ha jól tudom a proton elektron és a neutron egyaránt 3-3 kvarkból áll. Akkor hogy lesz egy protonból és egy elektronból egy neutron?"
Úgy, hogy részecskeütközéskor nem a két anyag egyesül, hanem a kvantum tulajdonságok összegződnek, és minden energiává alakul, és hirtelen addig nem létező részecskék keletkeznek, amiknek az összes kvantum tulajdonsága azonos. Tömeg, töltés, spin, mozgási energia. Tehát nem a meglévő golyóbisok alkotnak más struktúrát, hanem új golyóbisok keletkeznek, és semmilyen kvantum tulajdonság nem veszik el.
Azt ugye tudod, hogy egy neutron magában 7-8 perc alatt megsemmisül. Az atomok mégis megmaradnak. Hogyan lehetséges ez? Úgy, hogy a proton és a neutron között közlekedik az atommagban egy kölcsönhatás részecske, ami kvantum tulajdonságokat szállít az egyikből a másikba. Egy protonból neutron lesz, egy neutronból meg proton, és újra indul a stopperóra, hogy mikor bomlik le a neutron.
Amikor egy protonba (két U és egy D kvark) bepréselődik egy elektron, akkor az egyik U kvark D kvarkká változik, és egy két D és egy U kvarkból álló neutron lesz. Az elektron töltése elhasználódik, az elektron nem belekerül, hanem megsemmisül, és a felesleges tömeg és mozgási energia megteremt egy új részecskét, egy neutrinot. Az előtte nem volt sehol, addig nem létezett. Ő akkor teremtődött. Nem volt alkatrésze egyik részecskének sem. Ez arra utal, hogy a részecskék nem anyagok, hanem tiszta energiák, amik anyagnak néznek ki. Valójában nem részecskék ütköztek, hanem hullámok, amik energiából vannak. AZ anyagi megnyilvánulása minden részecskének csak egy arca az energiának, amit mutat. Képletesen szólva, ha az anyagok megfelelő energiával ütköznek, akkor az összes tulajdonságot a természet belerakja egy nagy kalapba és újra legózza belőle az anyagokat, amik az ütközésben részt vettek. Ebben az esetben az energia csak arra elég, hogy egyetlen kvarkot módosítson, így neutronosodik a proton, mert egy kvarkja megváltozik, és a maradék energiából csinál egy neutrínót a természet, és még jó nagy mozgási energia is marad neki az összenergiából, tehát az elrepül messzire jó gyorsan köszönés nélkül. És ha az össztömeget, meg mozgási energiát összeadod, meg a spint és töltést is, akkor az új részecskék pont ugyanazt adják ki, mint amikből keletkeztek. -
Drinkman #47 -
Drinkman #46 Ha visszaellenőrzöd rájössz hogy 716-al számolgattam. -
Vol Jin #45 "Meg akkor sem, ha a gravitaciot a centrifugalis ero 1 G nagysagrendjere csokkentene."
Ez egy fizika karó.
Nem kiegyenlítődés történne, hanem összeadódás. A gravitáció lefele húz, a forgás lendülete felfelé tol. Nagyobb lenne a súlyod, nem kevesebb.
Könnyen ellenőrizheted egy liftben. Ha elindul fölfele a lift, nagyobb súly fog nehezedni a lábadra, amíg gyorsul.