64
A grafikus és számjegyes minimalizálási módszer
-
cmsworld #64 A Pannon Egyetemre járok. -
 #63
#63
Te melyik főiskolára jársz? O.o -
mukievil #62 okés nemgond :), de azt hogy nemteljesen jó :D, azt azért fenntartom :) -
cmsworld #61 Belinkelem a korábban felvetett feladat megoldását, ha esetleg a későbbiekben valakinek hasonló problémája lenne. A megoldásért köszönet Mukievilnek!
-
mukievil #60 Tévedtem, kicsit bonyolultabb mint gondoltam! 16-osban már megtudom csinálni, de igy 32-esben még bonyolit egy kicsit a dolgon, ugyhogy ma nem hiszem hogy meglesz, de a hétvégén megcsinálom vmikor!!! -
cmsworld #59 Köszönöm, izgatottan várom! :) -
mukievil #58 Na megvan a megoldás, megcsinálom lefotozom és elküldöm :D de akkor jár a sör nekem :D:D, 3-4 év után nem megy már olyan könnyen :D ,de beugrott, kb két ora és megvan, mert még dolgom van! -
cmsworld #57 Ami a jegyzetemben volt azok olyanok, mint amiket először kérdeztem. Ilyet mint ez a legutóbbi más jegyzetekben sem találtam, őszintén szólván sehol, neten sem. Egy kidolgozott minta nincs erre sehol. De ha egyszer a vizsgán meg ezt kérik számon... -
cmsworld #56 "fel kell írnod az összeset egyenként"
Ez azt jelentené, hogy beírom az összeset a prímimplikáns táblázatba és megvalósítóm az összeset? -
mukievil #55 http://poppy.snu.ac.kr/~kchoi/class/lc_intro/two_level.pdf
itt van középtájon egy ekivalenciás megoldás (ekvivalencia =XNOR)
Sajna nemtudom tényleg megoldani, én már nem emlékszem erre! De ha ez neked tényleg kell, és a főiskolán tanulod, vagy egyetemen, akkor nyilván van jegyzeted amiben benne van, vagy megkérdezed a tanárod, vagy felsöbbéveseket, vagy évfolyamtársaidat, akik ebben benne vannak!
-
mukievil #54 http://www.freeweb.hu/nagyy/projects.html
itt van egy program, de csak az egyszerübbeket kezeli -
cmsworld #53 Azt olvastam egy jegyzetben hogy szimmetrikus függvényt kell rá felírni. Azonban a példa nem volt teljesen kidolgozva és erre valahogy nem igen sikerült felírni. Valaki megmutatná ennek a megoldását, mert ilyen típusúra sehol nem találok egy épkézláb kidolgozott feladatot. Előre is köszönöm! -
mukievil #52 Hát a számjegyesnél ugylátom erre gondolsz amit lejjebb linkeltem:
http://www.kobakbt.hu/jegyzet/DigitTechnika/Feladatok/html/qmc/qmc1.html
quine mclasky modszer vagy mi, de nem e legkönyebb modszer, könnyü hibázni is benne
És mint két kommenttel lejjebb irtam, "sakktábla szerü" elrendezésnél antivalencia kapuk vannak. Azaz egy üres egy egyes, egy üres egy egyes és igy tovább az egész táblára!
Sztem a megoldás az ez lenne:
A (antivalencia) B(antivalencia) C(antivalencia) D (antivalencia) E
A jelét sajna nemtudom, meg nem is lehet talán olyat irni ide
minden egyesre felirhato igazábol az 5 betüböl álló függvény
pl. A negált B C negált D E negált ez meghatároz egy egyest valahol
Ez mindegyikre felirható, aztán az azonossságokat használva, ki lehet az azonosokbol emelgetni betüket, meg különféle trükökkel le lehet vezetni hogy ez egy ANTIVALENCIA.
De az ilyenekre ránézésre rávágjuk!!! -
Hugh Hefner #51 hu a szamjegyes minimalizalas az melyik is? otletem sincs hol vannak a jegyzeteim, de ha jol emlekszem, akkor az az, amelyikben tobb oszlop van, akkor ha jol emlekszem akkor azt igy kell: (de vmi okos biztos megmondja, en vegulis nem infosnak tanulok) (igazából csak a metodikájára emlékszem, arra hogy mi miért van, az már nem nagyon van meg)
1. oszlop: fogod es megnezed, hogy kettes szamrendszerben hany 1-es használsz fel, és növekvő sorrendben felülről lefele írod fel, vonallal elválasztva
2. oszlop: itt a különbségeket nézed, azt nézed, hogy a számok között hol van olyan különbség, ami kettő hatványa. azért kell az első oszlop, mert úgy nézed, hogy az első oszlop első csoportjából hasonlítasz össze számot a második csoporttal. aztán a második csoportot a harmadikkal, és így tovább. és így a második oszlopba is csoportokban jönnek ki a számok, amit így jelölünk mondjuk, 4,6 (2), a 4-et és a 6-ot hasonlítottad össze, és a különbség 2.
3. oszlop: lövésem sincs : \ nem emlékszem már, de mintha valami olyan lenne, hogy egyértelművé teszed, és kizárod azt ami többször van, de tényleg nem akarok hülyeséget mondani.
mondjuk a te példádat nézve:
a faszom, ez egy köcsök feladat, nincs második oszlop, mondd meg a tanárodnak hogy egy geci, elkezdtem csinálni, az 1. oszlop megvan, a 2.-at nemtom, tényleg nincs pár. nézd meg karnaugh táblával, ha ott sincs, akkor ezt tényleg nem lehet, fel kell írnod az összeset egyenként -
mukievil #50 Sajna már nem emlékszem hogy hogy kell levezetni, de a megoldás itt van (lap alján):
"Bár erről még nem volt szó, az ilyen sakktábla-szerű Karnaugh-tábla antivalencia kapukat jelez:"
http://e-oktat.pmmf.hu/digtech32 -
cmsworld #49 pl.: Konkrét függvény: 0 3 5 6 9 10 12 15 17 18 20 23 24 27 29 30 Eddig ilyennel nem találkoztam és neten sem találok egy olyan jegyzetet sem amiben ehhez hasonló lenne. Ezt számjegyesen kellene minimalizálni. -
mukievil #48 Sajna most nincs időm rajzolgatni, neten meg nem találtam, de ha ezt tanultad, csak van rola valami jegyzeted!
Ezek csak nagyon alap dolgok amiket mondtam, a többit fejből meg már én sem tudom nagyon! -
mukievil #47 Pl az antivalenciánál, és az ekvivalenciánál nem párban vannak, de egyébként ha nincs pár, akkor nagy szivásod van :D, mert minden egyes egyest, egyenként kell, meghatározni!
-
Cat 02 #46 12 van ha jól emlékszem (mármint 6 és azoknak a negáltja) -
cmsworld #45 Számjegyes minimalizáláshoz az a kérdésem lenne, hogy mi van akkor ha olyan számok vannak megadva, hogy nem lehet párokat képezni belőlük. Olyankor mit kell csinálni? -
mukievil #44 Jajj, korán van még :), az nem egy 16os tábla :D, csak 8 négyzetből áll :D -
mukievil #43 Nem csak összesadás és szorzás van! Ez igazából digitális technika!
Létekzik: és, vagy, nem, kizáróvagy, kizáróés, ekvivalencia, antivalencia ...
(én már régen tanultam, lehet nem teljesen pontos amit irok)
A veitch tábla, 2 hatványai számau kis négyzetekből állnak! NEm teljesen értem a kérdést! Pl, a 16os tábla, az téglalap alakú!
Egyéb információk google
(boole algebra, logikai függvények, digitális technika alapjai) -
Hugh Hefner #42 jajbocsánat, itt nincsenek megoldott feladatok, vagy levette, vagy rosszul emlékszem, a 2. zh-s anyagrész van itt, az elsőből csak feladatok. ha gyakorolni szeretnél.
de amúgy a lényege h a lehető legnagyobb 2-es hatvány szerinti területet karikázd be (a szélek mintha összeérnének), és egyértelműen írd le, a lehető legkevesebb hurokkal, igen/nem szerint -
Hugh Hefner #41 tessék, itt is van pár feladat megoldva
http://bagira.iit.bme.hu/~tom/digit/viiia041.htm
username: digit
password: vifo1016
horváth tamás te meg szopjál lovat (elvileg nem lehetne kiadni a jelszót, lol) -
lotsopa #40 Csak összeadás és szorzás műveletek vannak értelmezve?
Ez a Veitch-tábla csak négyzetekből álló "nagy" négyzetként ábrázolható, értelmezhető. Nem lehet bonyolítani, kibővíteni? :) -
cmsworld #39 Igen, ezt beértettem annak. :) -
mukievil #38 Tehát az elsö ábrán, ez a C negált * D akart volna lenni!
Ellenkező esetben, minden szinezett négyzet a megoldás lenne (c negált + D) -
mukievil #37 Még egy hiba, van nálam is! Nem mind1, hogy szorzás vagy összeadás van a két betü között! A szorzás az és, az összeadás a vagy!!! -
cmsworld #36 Köszönöm a magyarázatokat. Na meg persze mindenki más segítségét is. -
mukievil #35 és még1, hogy érthető legyen az értelmezés is :
-
mukievil #34 áá, mégse maradt le, csak lassu a net sorry -
mukievil #33 bocsi lemaradt
-
mukievil #32 Egyébként mivel meg van határozva, melyik "betü" milyen értkű, ezért nyilván ha vki más értéket ad egy betünek , más értékek jön ki!
pl:
A=1
B=2
C=4
D=8
vagy forditva
A=8
B=4
C=2
D=1
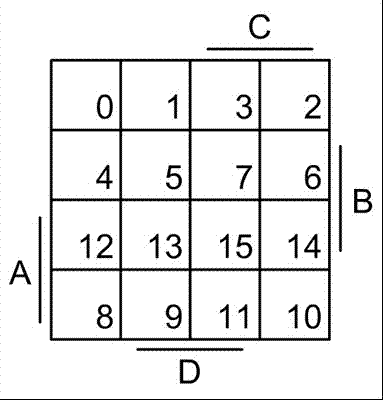
A 6. hozzászolásba lévő Veitch-tábla (a karnaugh tábla, az máshogy néz ki, de ugyanezt ábrázolja igazábol--->google) mivel hibásan van felirva, ezért nehezen értelmezhető!!!!
C=1
A=2
B=4
D=8
Itt egy helyes felirás , amin fel van tüntetve melyik mezőnek, mekkora bináris értéke van:
-
mukievil #31 A megoldás itt van :
http://www.kobakbt.hu/jegyzet/DigitTechnika/Feladatok/html/qmc/qmc1.html -
cmsworld #30 Ilyen módon ha valaki minimalizál egy logikai függvényt és a minimális alakból valaki más peremezést alkalmazva(mivel mindegy) megpróbálná visszanyerni az eredetit, akkor nem jó megoldásra jutna? -
Cat 02 #29 Teljesen mindegy, hogy melyik oldalon van peremezve. Bár általában úgy szokták, hogy jobb oldalt: AB, alul CD (vagy ABC,CDE ...) -
 #28
#28
szerintem ezért a sorozatgyilkos szövegért lassan nagyobb fejbebaszás járhatna, mint maga a szó elrontásáért :) -
cmsworld #27 Sajnos eléggé idő szűkében vagyok, így azzal hogy milyen formátumú képet linkelek nem annyira foglalkoztam. Ezzel a grafikus minimalizálással kapcsolatban pedig már csak ezt nem értem(mint ahogy írtam alább):
"Még azt szeretném megtudni, hogy a peremezése a táblának miért pont olyan ahogy a feladatomban volt? Lehetne másmilyen is vagy mitől függ ez?"
-
Cat 02 #26 Érdekes, hogy vizsgaidőszakig csak Karnaugh-tábláig juttok.
Mi infosok is eljutottunk a flipflopokig és a villanyosok is nálunk. -
Szeszmester #25 Egyenlőre a sorozatgyilkos vág fel, mielőtt beletesz a formalinos üvegbe.
Te az egyelőre szót kerested.
Amúgy, ha már a Karnaugh-táblával is gondok vannak (és BMP-t linkelsz), talán értékeld át ezt az egyetemet. Jóval cifrább dolgok is lesznek ott.