49
a káosz ábrázolása képen, matematikai képletek segítségével
-
Csesza #9 énis :DDDDDDDddd:ASDasdasdasd -
 #8
#8
Én meg az alatta lévőt 
-
 #7
#7
A zöldet betettem háttérnek:D
ColdFire: Én is aszittem először, hogy Cagivamito rokona nyitotta Különös traktorok néven, de úgy tűnik mégse:D -
 #6
#6


Ezeket es a hasonlokat regen nagyon szerettem:) Tobb mint 20 eve (jaj:D), meg Commodore-on foleg ilyenekkel szorakoztam, pontosabban fraktalok, Mandelbrot megoldasok, es kulonfele mozgasok abrazolasa hasonlo modon:) Persze BASIC, a grafika meg az Commodore, vagyis nem ilyen szep:P De utana az elso PC-knel meg Pascal-on is probalkoztam ezel-azal;)
Most mar, inkab csak a kepeket nezegetem:D -
 #5
#5
azthittem Attack Traktorok :c -
mod #4 Nem annyira értem a lényegét, de gyönyörűek. -
 #3
#3
érdekes.de ez nekem bonyolult -
blackgamer #2 lehagyott pár képet az első hozzászólásból 
nem tudom miért, megpróbálom újra linkelni azt a részt...
Az egyszerű attraktorok fix pontba jutnak, vagy periodikusan ismétlődnek.
példa egyszerű attraktorra:
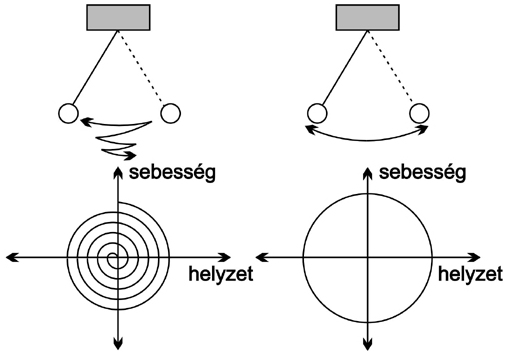
ha egy súrlódásmentes inga mozgását ábrázoljuk
koordináta rendszerben felvesszük a kilengés helyzetét (mondjuk x tengelyre) és a sebességét (y tengelyre)
ekkor a képen egy hurok lesz, ami állandóan ismétli önmagát
ha belevesszük a súrlódást is, egy spirált kapunk ami a nyugalmi pont fele halad
A különös attraktor ezzel szemben sose ismétli önmagát és nem ér fix ponthoz sem.
Egy végtelen hosszú vonal (ami nem metszi magát), véges területen (mint a fraktál is tulajdonképpen)
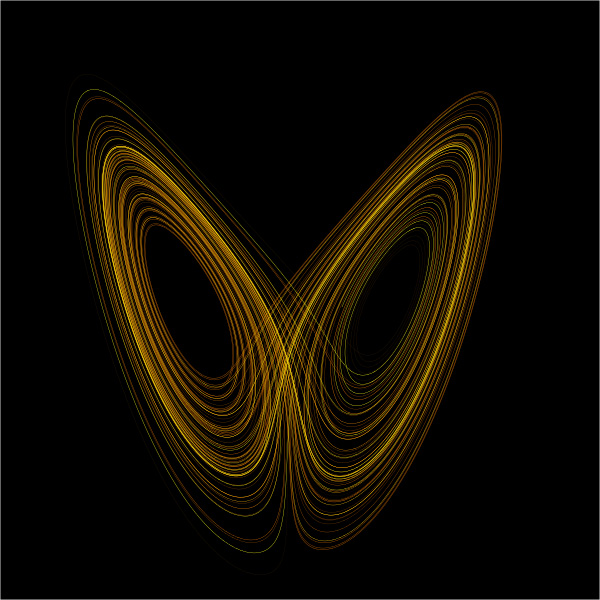
Az első Edward Lorenz nevéhez fűződik, 1963-ban rajzolta a nevét viselő attraktort, melyre 1971-ben figyeltek fel igazán.
Ő az időjárás szabálytalanságát és hosszú távú előrejelzését vizsgálta. Tőle ered a Pillangó-hatás: "Egy pillangó szárnycsapása okozhat tornádót Texasban?"
vagyis a kis input változás nagy output eltérést okozhat, de ebbe nem mennék bele részletesen mert több káosz elmélet topik is létezik...
a lényeg: Lorenz olyan rendszert keresett amiben szintén megfigyelhető a káosz
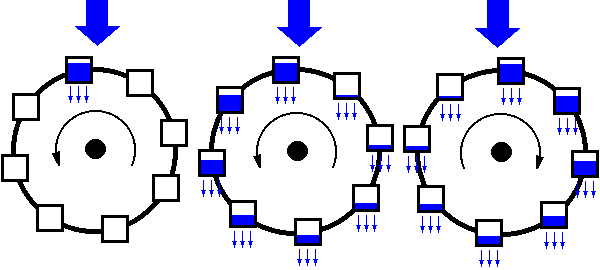
ekkor bukkant a vízkerékre, amibe fentről folyik a víz, a dézsákból pedig lassan kifelé
ha gyorsabban engedjük a vizet, egy bizonyos ponton már nem tud elég víz befolyni mert annyira felgyorsult a kerék, miközben gyors forgás miatt kevesebb víz folyik ki és a kerék forgási iránya megváltozik
ezt a mozgást a Lorenz attraktor ábrázolja (a "pillangó" két szárnya az egyes irányok)
Később több tudós is talált különös attraktorokat a saját kutatási területén. -
blackgamer #1 Sziasztok!
Az attraktorokat időben változó rendszerek képként való ábrázolására használjuk.
Amikor egy tudós egy fázistérbeli képet néz, képzeletében felidézheti magát a rendszert: ez a hurok ahhoz a periodicitáshoz tartozik; ez a csavarodás annak a változásnak felel meg; ez az üres terület ezt és ezt a fizikai lehetetlenséget tükrözi.
A fázistérben egyetlen pont jeleníti meg mindazokat az ismereteket, amelyeket a dinamikai rendszer valamely időpillanatban felvett állapotáról tudunk.
Az egyszerű attraktorok fix pontba jutnak, vagy periodikusan ismétlődnek.
példa egyszerű attraktorra:
ha egy súrlódásmentes inga mozgását ábrázoljuk
koordináta rendszerbe felvesszük a kilengés helyzetét (mondjuk x tengelyre) és a sebességét (y tengelyre)
ekkor a képen egy hurok lesz, ami állandóan ismétli önmagát
ha belevesszük a súrlódást is, egy spirált kapunk ami a nyugalmi pont fele halad
A különös attraktor ezzel szemben sose ismétli önmagát és nem ér fix ponthoz sem.
Egy végtelen hosszú vonal (ami nem metszi magát), véges területen (mint a fraktál is tulajdonképpen)
Az első Edward Lorenz nevéhez fűződik, 1963-ban rajzolta a nevét viselő attraktort, melyre 1971-ben figyeltek fel igazán.
Ő az időjárás szabálytalanságát és hosszú távú előrejelzését vizsgálta. Tőle ered a Pillangó-hatás: "Egy pillangó szárnycsapása okozhat tornádót Texasban?"
vagyis a kis input változás nagy output eltérést okozhat, de ebbe nem mennék bele részletesen mert több káosz elmélet topik is létezik...
a lényeg: Lorenz olyan rendszert keresett amiben szintén megfigyelhető a káosz
ekkor bukkant a vízkerékre, amibe fentről folyik a víz, a dézsákból pedig lassan kifelé
ha gyorsabban engedjük a vizet, egy bizonyos ponton már nem tud elég víz befolyni mert annyira felgyorsult a kerék, miközben gyors forgás miatt kevesebb víz folyik ki és a kerék forgási iránya megváltozik
ezt a mozgást a Lorenz attraktor ábrázolja (a "pillangó" két szárnya az egyes irányok)
Később több tudós is talált különös attraktorokat a saját kutatási területén.
Akit jobban érdekel a téma, mindenképpen olvasson utána. (tervezem egy új topik nyitását ott majd ajánlok könyvet...)
Amiért nyitottam a topikot:
Ezek az attraktorok lélegzetelállító képek tudnak lenni.
Kicsit mások mint a fraktálok, itt nem látni mérettartományban ismétlődést.
Sokat lehet velük bütykölni, aki kicsit is ért a programozáshoz bármilyen grafikát megjelentetni képes nyelven készíthet látványos attraktort, sok képlet van a neten.
Akik próbálkozni szeretnének, több káosz programot találhatnak.
Én a Chaoscope nevű programot ajánlanám elsőre, érdemes a gallery menüpontba is bekukucskálni
indulás után New->megadod a típust, majd jobbra fent húzgálod a csúszkát és voila! kész a gyönyörű kép (ha a képen nyomod a gombot és mozgatod akkor térben fordul)
szal, jöhetnek ide a mestermunkák, plusz bármi a témához illő dolog
remélem nem voltam túl hosszú, álljon itt pár kép amit a netről halásztam...
ui. szeretném figyelmetekbe ajánlani a fraktál topikot is!
Lorenz attraktor paramétereinek időbeni változtatása (youtube)
mozgatás térben (youtube)
[center]