a káosz ábrázolása képen, matematikai képletek segítségével
-
blackgamer #2 lehagyott pár képet az első hozzászólásból 
nem tudom miért, megpróbálom újra linkelni azt a részt...
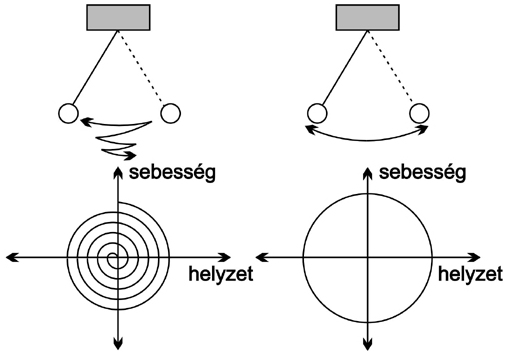
Az egyszerű attraktorok fix pontba jutnak, vagy periodikusan ismétlődnek.
példa egyszerű attraktorra:
ha egy súrlódásmentes inga mozgását ábrázoljuk
koordináta rendszerben felvesszük a kilengés helyzetét (mondjuk x tengelyre) és a sebességét (y tengelyre)
ekkor a képen egy hurok lesz, ami állandóan ismétli önmagát
ha belevesszük a súrlódást is, egy spirált kapunk ami a nyugalmi pont fele halad
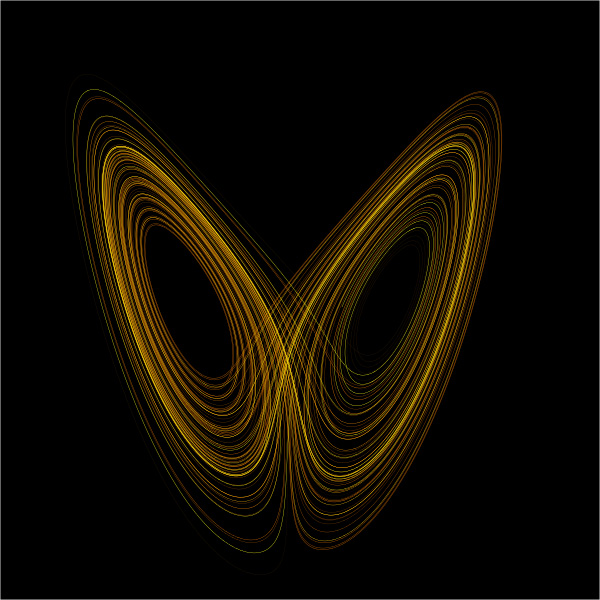
A különös attraktor ezzel szemben sose ismétli önmagát és nem ér fix ponthoz sem.
Egy végtelen hosszú vonal (ami nem metszi magát), véges területen (mint a fraktál is tulajdonképpen)
Az első Edward Lorenz nevéhez fűződik, 1963-ban rajzolta a nevét viselő attraktort, melyre 1971-ben figyeltek fel igazán.
Ő az időjárás szabálytalanságát és hosszú távú előrejelzését vizsgálta. Tőle ered a Pillangó-hatás: "Egy pillangó szárnycsapása okozhat tornádót Texasban?"
vagyis a kis input változás nagy output eltérést okozhat, de ebbe nem mennék bele részletesen mert több káosz elmélet topik is létezik...
a lényeg: Lorenz olyan rendszert keresett amiben szintén megfigyelhető a káosz
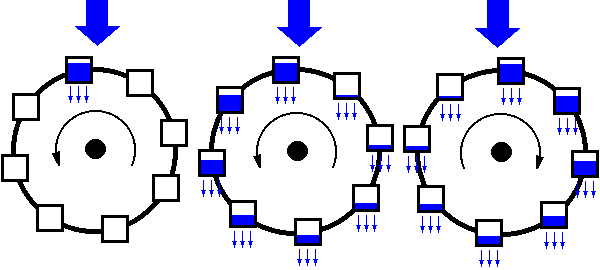
ekkor bukkant a vízkerékre, amibe fentről folyik a víz, a dézsákból pedig lassan kifelé
ha gyorsabban engedjük a vizet, egy bizonyos ponton már nem tud elég víz befolyni mert annyira felgyorsult a kerék, miközben gyors forgás miatt kevesebb víz folyik ki és a kerék forgási iránya megváltozik
ezt a mozgást a Lorenz attraktor ábrázolja (a "pillangó" két szárnya az egyes irányok)
Később több tudós is talált különös attraktorokat a saját kutatási területén.