MTI
A folyami kavics kopásának modelljét írták le magyar tudósok

A folyami kavics alakváltozását írták le magyar matematikusok és egy amerikai geofizikus, felfedezésük segítségével a Marson talált kavicsok formájából könnyen lehet következtetni a hajdan ott folyó víz sebességére és más jellemzőire.
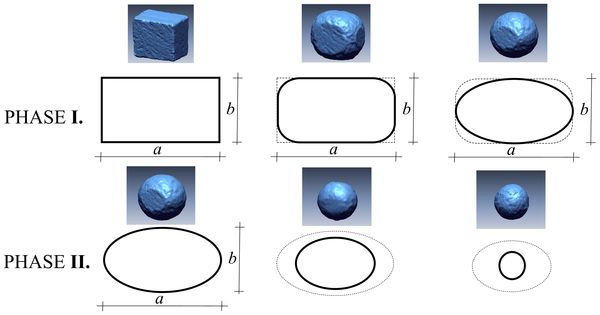
A folyók medrében található kavicsok az alsóbb szakaszokban többnyire kisebbek és gömbölyűbbek. A kavicsok felülete simára kopik, ahogy a folyó sodorja őket, ám vitatták az okát, miért kisebbek a kövek az alsó szakaszokon: elképzelhető, hogy a kopás a méretüket is csökkenti, de az is lehet, hogy csak a kisebbeket szállítja magával a víz. A Pennsylvaniai Egyetem Douglas Jerolmack geofizikus vezette kutatócsoportja a Budapesti Műszaki Egyetem matematikusainak közreműködésével kimutatta, hogy a jelenségben a kopás játssza a főszerepet, ennek pedig két jól elkülöníthető fázisa van: a kőről először lecsiszolódnak az élek és a kiálló részek, eddig a mérete nem változik. Ezután kezdi csökkenteni a kavics méretét a kopás - olvasható a kutatóknak a PLoS One tudományos portálon megjelent tanulmányában.
A két kutatócsoport az interneten bukkant egymásra. "Évek óta foglalkozunk a kövek formálódásának elméleti aspektusaival, az amerikai kollégák pedig a jelenség geológiai vonatkozásaival. Az egyik publikációnk feltűnt nekik, megkerestek bennünket, és innentől kezdve igen szoros volt az együttműködés. Mi a matematika oldaláról érkezünk, ők a geológia oldaláról, mindkét fél érdeklődik a másik területe iránt is - magyarázta az MTI kérdésére Domokos Gábor, a magyar kutatócsoport vezetője, a Budapesti Műszaki Egyetem tanára, a Gömböc nevű szerkezet Várkonyi Péterrel közös megalkotója.
Matematikai modellel sikerült megmagyarázni egy nagyon régi geológiai paradoxont: a köveknek a terepen általában a centiméterben mért szélességét és hosszát szokták megállapítani, és azt tapasztalták, hogy a folyók felső szakaszain ez a méret szinte nem változik, pedig a kavicsok jelentős kopáson mentek keresztül. Ezt a megfigyelést sikerült most egyszerű, jól érthető matematikai modellel megindokolni - közölte a kutató. "A kavicsoknak először az éles részét távolítja el a kopás, ez a folyamat pedig erős párhuzamot mutat a hővezetéssel, ami nem más, mint a hő térbeli és időbeli terjedése. A mi modellünkben a hőmérsékleti kiugrásnak a kavics görbülete felel meg, tehát például a kavicson egy csúcs egy kiugróan magas hőmérsékletű ponttal áll párhuzamban, és ez a kis helyen koncentrált hő igen gyorsan terjed szét egy testben" - hangsúlyozta Domokos.
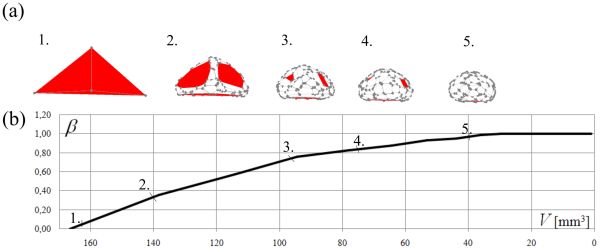
Ez nemcsak formai analógia, maguk a jelenséget leíró egyenletek is rokonok egymással, csak a hővezetést sokkal kimerítőbben vizsgálták, mint a bonyolultabb geometriai jelenségeket. Nagyon szoros kapcsolatot mutat a két jelenség viselkedése. Először egy gyors fázist látunk, amikor a hő szétterjed a testben mindenhová, és utána jön egy lassú kiegyenlítődési fázis. Geometriailag ez az élek gyors kopását követő lassú, a gömbhöz közelítő formaváltozásnak felel meg - állapította meg a kutatócsoport.
A jelenséget matematikai egyenletek támasztják alá. Richard Hamilton, a Columbia Egyetem világhírű matematikusa már az 1990-es években megsejtette, hogy a geometriai egyenletek két jól elkülönült fázist jósolnak meg. Sem gépi számításra, sem kísérleti adatokra nem támaszkodott, kizárólag matematikai eszközökkel jutott erre a következtetésre. Szabad kézzel rajzolt vázlatban rögzítette, szerinte hogyan zajlik a folyamat, és ezt a sejtést sikerült húsz évvel később a fizikai valóságban igazolni - világított rá a magyar kutató.
A felfedezés jelentőségét így foglalta össze: ismét bebizonyosodott, hogy a matematika a természet nyelve, tehát érdemes matematikai modelleket vizsgálni, mert megmagyarázzák a természeti jelenségeket, szép példa erre a folyami kavicsok kopásának folyamata. A kutatás másik üzenete gyakorlati jellegű. "Egy kavicsra ránézve a legfontosabb az a kérdés, hogy miként alakulhatott ki formája, vagyis aktuális állapota, a NASA marsi küldetésének egy fontos témája is ez" - húzta alá a professzor.
"Mi egy egyszerű és határozott állítást tettünk, amivel ez a kérdés ha nem is tökéletesen, de részben megválaszolható. Mivel a tanulmányunkban leírt két fázis élesen elkülönül, azt gondoljuk, ha több marsi kavicsot vizsgálunk, egyértelműen meg lehet mondani, hogy azok melyik fázisban vannak, milyen lehetett a kopástörténetük, mennyi ideig voltak vízben, hogy folyt a víz. A Mars esetében a rég eltűnt víz folyásának sebességére és egyéb jellemzőire is könnyen tudunk következtetni a kavicsok tulajdonságaiból - összegezte Domokos Gábor.
A folyók medrében található kavicsok az alsóbb szakaszokban többnyire kisebbek és gömbölyűbbek. A kavicsok felülete simára kopik, ahogy a folyó sodorja őket, ám vitatták az okát, miért kisebbek a kövek az alsó szakaszokon: elképzelhető, hogy a kopás a méretüket is csökkenti, de az is lehet, hogy csak a kisebbeket szállítja magával a víz. A Pennsylvaniai Egyetem Douglas Jerolmack geofizikus vezette kutatócsoportja a Budapesti Műszaki Egyetem matematikusainak közreműködésével kimutatta, hogy a jelenségben a kopás játssza a főszerepet, ennek pedig két jól elkülöníthető fázisa van: a kőről először lecsiszolódnak az élek és a kiálló részek, eddig a mérete nem változik. Ezután kezdi csökkenteni a kavics méretét a kopás - olvasható a kutatóknak a PLoS One tudományos portálon megjelent tanulmányában.

A két kutatócsoport az interneten bukkant egymásra. "Évek óta foglalkozunk a kövek formálódásának elméleti aspektusaival, az amerikai kollégák pedig a jelenség geológiai vonatkozásaival. Az egyik publikációnk feltűnt nekik, megkerestek bennünket, és innentől kezdve igen szoros volt az együttműködés. Mi a matematika oldaláról érkezünk, ők a geológia oldaláról, mindkét fél érdeklődik a másik területe iránt is - magyarázta az MTI kérdésére Domokos Gábor, a magyar kutatócsoport vezetője, a Budapesti Műszaki Egyetem tanára, a Gömböc nevű szerkezet Várkonyi Péterrel közös megalkotója.
Matematikai modellel sikerült megmagyarázni egy nagyon régi geológiai paradoxont: a köveknek a terepen általában a centiméterben mért szélességét és hosszát szokták megállapítani, és azt tapasztalták, hogy a folyók felső szakaszain ez a méret szinte nem változik, pedig a kavicsok jelentős kopáson mentek keresztül. Ezt a megfigyelést sikerült most egyszerű, jól érthető matematikai modellel megindokolni - közölte a kutató. "A kavicsoknak először az éles részét távolítja el a kopás, ez a folyamat pedig erős párhuzamot mutat a hővezetéssel, ami nem más, mint a hő térbeli és időbeli terjedése. A mi modellünkben a hőmérsékleti kiugrásnak a kavics görbülete felel meg, tehát például a kavicson egy csúcs egy kiugróan magas hőmérsékletű ponttal áll párhuzamban, és ez a kis helyen koncentrált hő igen gyorsan terjed szét egy testben" - hangsúlyozta Domokos.

Ez nemcsak formai analógia, maguk a jelenséget leíró egyenletek is rokonok egymással, csak a hővezetést sokkal kimerítőbben vizsgálták, mint a bonyolultabb geometriai jelenségeket. Nagyon szoros kapcsolatot mutat a két jelenség viselkedése. Először egy gyors fázist látunk, amikor a hő szétterjed a testben mindenhová, és utána jön egy lassú kiegyenlítődési fázis. Geometriailag ez az élek gyors kopását követő lassú, a gömbhöz közelítő formaváltozásnak felel meg - állapította meg a kutatócsoport.
A jelenséget matematikai egyenletek támasztják alá. Richard Hamilton, a Columbia Egyetem világhírű matematikusa már az 1990-es években megsejtette, hogy a geometriai egyenletek két jól elkülönült fázist jósolnak meg. Sem gépi számításra, sem kísérleti adatokra nem támaszkodott, kizárólag matematikai eszközökkel jutott erre a következtetésre. Szabad kézzel rajzolt vázlatban rögzítette, szerinte hogyan zajlik a folyamat, és ezt a sejtést sikerült húsz évvel később a fizikai valóságban igazolni - világított rá a magyar kutató.
A felfedezés jelentőségét így foglalta össze: ismét bebizonyosodott, hogy a matematika a természet nyelve, tehát érdemes matematikai modelleket vizsgálni, mert megmagyarázzák a természeti jelenségeket, szép példa erre a folyami kavicsok kopásának folyamata. A kutatás másik üzenete gyakorlati jellegű. "Egy kavicsra ránézve a legfontosabb az a kérdés, hogy miként alakulhatott ki formája, vagyis aktuális állapota, a NASA marsi küldetésének egy fontos témája is ez" - húzta alá a professzor.
"Mi egy egyszerű és határozott állítást tettünk, amivel ez a kérdés ha nem is tökéletesen, de részben megválaszolható. Mivel a tanulmányunkban leírt két fázis élesen elkülönül, azt gondoljuk, ha több marsi kavicsot vizsgálunk, egyértelműen meg lehet mondani, hogy azok melyik fázisban vannak, milyen lehetett a kopástörténetük, mennyi ideig voltak vízben, hogy folyt a víz. A Mars esetében a rég eltűnt víz folyásának sebességére és egyéb jellemzőire is könnyen tudunk következtetni a kavicsok tulajdonságaiból - összegezte Domokos Gábor.