20
Minden terület, ahol felmerül
-
#20
majd holnap kigúglizom:P
jó éjt:D -
debussy #19 mondj Tolsztojtól műveket és szólok, hat talált :) -
#18
Hallottam erről már és csak betippeltem:D -
debussy #17 És tudod is, hogy melyik mű, vagy csak betippeltél két nagy oroszt? :P -
debussy #16 Igen
Dosztojevszkij nagy kedvencem, de a megfejtés Tolsztoj -
#15
Dosztojevszkij vagy Tolsztoj írta? :D -
debussy #14 Van egy mű, amiben a szereplő élete a könyv 1/3 része, a haldoklása pedig a 2/3 része. Ugyanis ez alatt az idő alatt kezd el tartalmasan gondolkodni és ekkor kap értéket rövidke maradék ideje. Na ki tudja melyik könyv? (Segítek: orosz) -
#13

-
 #12
#12
Ja, hát ez divat kategória. Vannak építészek, akik szeretik, vannak, akik nem.
Zenében is hasonlóképp.
A lényeg, hogy ebből aztán kurvára semmi értelmeset nem lehet levezetni, és ráadásul még 100% szubjektív is.
Nem véletlenül halt el ez a filozófiai irányzat... -
#11
igen, de van hogy zenében pont a disszonancia, vizuálisan pedig
az asszimetria vagy valamilyen káosz ad élményt:) -
 #10
#10
Annyi szerintem a párhuzam, hogy a zene a hangok harmóniája, az aranymetszés meg a látványé. -
#9
A zenében semmi haszna az aranymetszésnek. -
 #8
#8
Pepsiék szeretik, úgy tűnik... :)
PDF (kifejtve, hogy hogyan aranymetszés, meg mitmiért) -
 #7
#7
Annak idején ilyen oldalarányokkal (0,62 1 1,62) terveztem hangfalakat, azóta ezt a módszert megszüntettem, mert rezonanciák szempontjából van előnyösebb is. -
 #6
#6
"Azt mondták, hogy az õket körülölelõ világban ugyanúgy, mint bennünk, valamint a zenében is megtalálható a számok harmóniája, tehát ha tanulmányozzuk a zenében rejlõ harmóniát, akkor az élet dolgainak megértése is könnyebbé válik. "
Itt jön be az, hogy amikor valaki egy témával többet foglalkozik annál, mint ami egészséges lenne, akkor kissé beleőrül. Amikor már azt hiszi, hogy körülötte, illetve a figyelmének tárgya körül forog a világ.
Hoznak 3 példát a természetből, aztán ráfogják, hogy ez olyan, mint a zene (ami _szándékosan_ egy harmonikus dolog), és ebből akarják levezetni a világ nagy dolgait.
Nem csodálom, hogy erről a pitagoreizmusról még soha nem hallottam, elég szűk réteg követheti ezt a filozófiai irányzatot... -
 #5
#5
aranymetszés
lényegében arányok arra hogy mit tartunk esztétikusnak -
GM Jojo #4 Sokan nem ismerik ezt a kifejezést pedig életünkben sokszor találkozunk vele.
Itt egy kis izelítő:
Az aranymetszés számai a matematikában és a zenében is egyaránt elõfordulnak. Aranymetszés akkor jön létre, ha az egész (egy kicsi és egy nagyobb rész összege) úgy aránylik a nagyobb részhez, mint a nagyobb a kisebbhez. A nagyobb rész mértani középarányossá válik. Ha az egész egyenlõ eggyel, akkor a nagyobb rész egyenlõ 0,618, míg a kisebb rész 0,382 közelítõ értéket vesz fel, ugyanis az aranymetszés aránya irracionális szám (0,618034…). Bármely távolság aranymetszete az egész távolság és a 0,618 szorzása során megkapható.
Az 1200-as évek elején egy pisai tudós a számok különleges sorozatát fedezte fel. Ez a legegyszerûbb, egész számokkal kifejezhetõ aranymetszéssor:1; 2; 3; 5; 8; 13; 21; 34; 55; 89… A matematika – a pisai tudós után – Fibonacci-számsornak nevezte el. A lényege:
1+2=3
2+3=5
3+5=8
5+8=13...
A sorban elõre haladva két szomszédos szám hányadosa egyre jobban megközelíti az aranymetszést, például 13/21=0,619 és 21/34=0,618 stb., illetve bármely szám négyzete azonos (1 különbséggel) az elõtte és utána álló két szám szorzatával.
Az aranymetszés számait sok tudományban és a legkülönbözõbb mûvészetekben fedezhetjük fel. Nézzünk néhány példát.
Matematika: Kepler-háromszög: ha a derékszögû háromszög magasságát behúzzuk, az átfogó a már ismert arányban oszlik fel, és derékszögû háromszögek keletkeznek, amivel a sor folytatható: így lényegében az átfogó mértani közepét kapjuk meg, amelyet már a pitagoreusoknál is megemlítettünk.
Míg a kör ívére a sugarat hatszor, addig a sugár aranymetszését pontosan tízszer lehet rámérni.
Biológia: a Nautilus egy tengeri csigafaj, melynek csodálatosan szabályos héja van. Bárhogyan is húzunk vonalat a középponton áthaladva, mindegyik metszés- (AC:DB=FG:EG) arány aranymetszés.
A fenyõtoboz korongján a spirálvonalak olyan rendszere fut a középponttól jobbra és balra, amelyben a csigavonalak száma mindig a Fibonacci-sor értékeit veszi fel: 3; 5; 8; 13; 21… Más tobozfajtákban ez 5; 8; 13; 21; 34… stb.
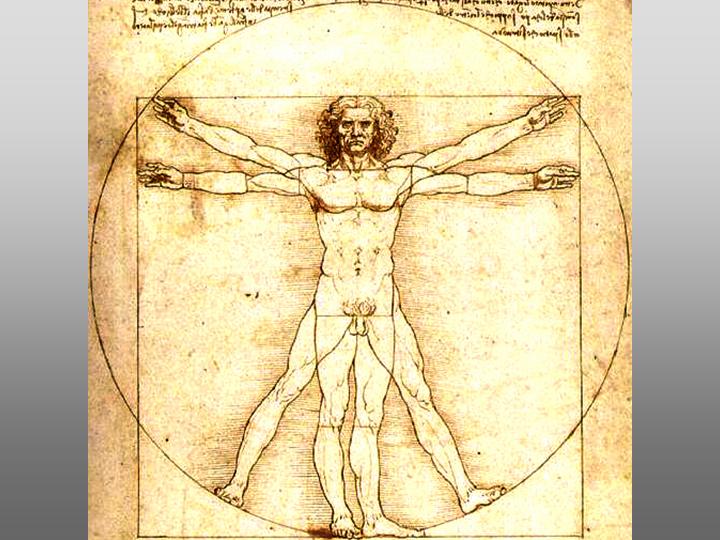
Végül egy utolsó példa a biológia területérõl: az emberi test aranyközéppontja a köldök, a felsõtesté a gégefõ, és az arcé a szemöldökvonal.
Mûvészetek: talán a legjelentõsebbek az építészet csodái.
Az ókori Egyiptomban a piramisok mindegyikében éppen az aranyszög (vagyis „a szinusz és a kotangensgörbék találkozási pontja” 51o49´38”) az oldallapok dõlésszöge az alaphoz képest.
A következõ állomás az ókori Görögország: az atheni Pantheon több szempontból is érdekes: a statikáját az adja, hogy két négyzet rajzolható bele, míg a dinamikája az aranymetszésbõl ered (A, B, C, D… H pontok).
Az építõmûvészet egyik legnagyobb remeke a Szent Péter Bazilika, ahol több helyen felfedezhetõk érdekes arányok. Itt csak egyet emelek ki, a csúcsán lévõ keresztet. Itt Michelangelo a görög stílust követte, miszerint „a Föld (a négyzet) egyensúlyban van az Éggel (a kör)”, tehát kerületük egyenlõ. Így a háromszög szöge egyenlõ az aranyszöggel (51o49´38”).
Ebbõl származik a jellegzetes szerkezeti háló, amely meghatározza a mûalkotás felépítését. Az alapháló három köre aranymetszés-viszonyban van egymással.
Az irodalomból is egy példa: Dante Isteni színjátéka, amelynek 100 énekébõl a 62.-ben (amely a 100-nak aranymetszete) válik el Dante Vergiliustól, és itt csatlakozik hozzá Beatrice, hogy a Paradicsomon végigkísérje.
Végül a számomra legfontosabbak, a zene arányosságai: a zenetörténeti korszakok során többször is érvényesültek a szerkesztés rendjében.
Elsõként Ockeghem (flamand születésû zeneszerzõ kb. 1420–1495 között) alkalmazta tudatosan. A késõbbi idõk legjelentõsebb zeneszerzõi: Bartók Béla és Kodály Zoltán, akik alkalmazták az aranymetszés kínálta lehetõségeket. LendvaiErnõ több mûvükben is felfedezte a 0,618 és 0,328 aránypár szerinti szerkezeti felosztást.
Vegyünk néhány példát: Kodály Psalmus Hungaricusa 395 ütembõl áll, a 245. vagyis a 395x0,618-adik taktus kezdetével esik egybe a mû eszmei mondanivalójának kimondása: „Istenben vessed bizalmadat.”
Ugyanígy fedezhetõ fel Bartók kétzongorás-ütõhangszeres szonátájának a reprízbelépés pontján, hogy az ütemfelosztás aranymetszés: tehát a 443-ütemes mû 274. ütemében történik.
Mûveik közül még sok darabban van az aranymetszés szerinti ütemfelosztásnak jelentõsége (fordulópontként, tetõpontként). Néhány ilyen darab: Mese a kis légyrõl; Tört hangzatok; Háry János.
A pitagoreusok filozófiája az aranymetszés „értelmezésével” teljesedett ki. Azt mondták, hogy az õket körülölelõ világban ugyanúgy, mint bennünk, valamint a zenében is megtalálható a számok harmóniája, tehát ha tanulmányozzuk a zenében rejlõ harmóniát, akkor az élet dolgainak megértése is könnyebbé válik.
-
 #3
#3
füzeteken a vignetta.
De mondok még egyszerűbbet. Az emberi test. -
 #2
#2
Szerintem írhatnál róla több dolgot is... :)
Esetleg saját vélemény, bővebben kifejtve. :) -
GM Jojo #1 Szerintem ez is egy érdekes téma. Gyakorlatilag az élet bármely területén megtalálhatjuk.
Kíváncsian várom mit tudtok ebben az érdekes témában. Ha vki esetleg nem hallott még erről, ajánlom a Pi című filmet.