Eddig úgy hitték, nincs semmi, ami hidegebb lenne az abszolút nulla foknál, német kutatók azonban elérték, hogy egy anyagnál negatív hőmérséklet alakuljon ki, átültetve egy eddig csupán elméleti síkon mozgó kísérletet a gyakorlatba. A felfedezés megingathatja elképzeléseinket a hőmérsékletről és segíthet megismerni olyan különös entitásokat, mint a sötét energia, valamint a szubatomi részecskék közötti kölcsönhatások.

Hagyományos értelemben véve nincs semmi különös a negatív hőmérsékletekben, az utóbbi napokban uralkodott fagypont alatti hőmérséklet is jó példa erre, a tudományos hőmérsékleti skálán azonban az abszolút nulla -273,15 Celsius foknak felel meg. A Kelvin skálán a hőmérsékletet a részecskék kinetikus energiája határozza meg, ezért egy lassú részecskékből álló gáz hidegebb, mint egy gyorsan mozgó részecskéktől hemzsegő. Az abszolút nulla annak a pontnak felel meg, amint a részecskék mozgása teljesen megáll, aminél semmi nem lehet hidegebb.

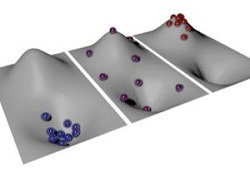Ez azonban még nem a teljes történet. A hőmérséklet a részecskék energiáinak a gázon belüli eloszlásától is függ, meghatározva entrópiájukat, vagy rendezetlenségüket. Abszolút nulla felett az energia hozzáadás az entrópia növelésének felel meg. Képzeljünk el egy hegyet és mellette egy völgyet (képünkön), melyen a csúcs egy részecske energiájának felel meg, és az esély, hogy adott magasságon egy részecskét találunk, az entrópiát testesíti meg. Abszolút nullánál a részecskék mozdulatlanok és egyikük sem rendelkezik energiával, ezért a völgy aljában helyezkednek el, minimális entrópiát tanúsítva. A gáz melegítésével a részecskék átlagos energiája nőni kezd, egyes részecskék rengeteg többlet energiához jutnak, míg mások csak egészen kevéshez.

Szétszóródva a hegy oldalán, a részecskék különböző energiákkal rendelkeznek, ezért a rendezetlenség magasabbá válik. A hőtanban alkalmazott entrópia meghatározása szerint a legmagasabb lehetséges pozitív hőmérséklet felel meg a rendszer legrendezetlenebb állapotának. Ez egyenlő számú részecskét jelentene a "táj" minden egyes pontján. Ha tovább növeljük az energiát, az entrópia ismét csökkenni kezd, mivel a részecskék egyenletes eloszlása megszűnik, eredményként ez a pont jelenti a pozitív hőmérsékleti skála végét.

Az alapelveket tekintve azonban lehetséges lenne a részecskék hevítése, miközben az entrópiát csökkentjük. Mivel ez megszegi az energia-entrópia kölcsönösséget, ez jelzi a negatív hőmérsékleti skála kiinduló pontját, ahol az energia eloszlás megfordul. Ahelyett, hogy a legtöbb részecske alacsony energiával, míg néhány magasabbal rendelkezik, a többségé a magas energia és csak néhány részecske alacsony energiájú. A negatív skála végét akkor érjük el, amikor minden részecske az energia-hegy csúcsán van.

Az így kapott hőmérő több mint szokatlan: a skála nulláról indul, plusz végtelenig kúszhat fel, majd mínusz végtelenre ugrik, mielőtt a negatív számok nőni kezdenének egészen addig, míg el nem érik a negatív abszolút nullát, amivel az összes részecske eléri a hegy csúcsát. "Az általunk ismert hőmérsékleti skála nullánál kezdődik és végtelenig megy fel, itt azonban még nincs vége" - mondta dr. Ulrich Schneider, a müncheni Ludwig Maximilian Egyetem fizikusa, a kísérlet vezetője.

A negatív birodalomba való belépés érdekében Schneider és munkatársai atomokat hűtöttek az abszolút nulla közelébe és egy vákuumba helyezték azokat. Ezután lézerekkel egy energia-völgy görbéje mentén rendezték el az atomokat úgy, hogy többségük alacsony energiaállapotú legyen. Az atomok taszították egymást, így biztosítva, hogy ne mozduljanak el a helyükről. Ezután a kutatócsoport negatívvá változtatta ezt a pozitív hőmérsékletet. Először vonzást idéztek elő az atomoknál, majd a lézerekkel megváltoztatták energiaszintjeiket, a többséget a magas tartományba helyezve át, így a völgyből egy energia-hegyet alkottak. Az eredmény egy fordított energia eloszlás lett, ami a negatív hőmérsékleteket jellemzi.

Az atomok nem veszthettek energiát "legurulva" erről a hegyről, mivel ehhez növelniük kellett volna a kinetikus energiájukat, erre azonban a vákuum miatt nem nyílt lehetőségük, illetve külső energiaforrás sem állt a rendelkezésükre. "Létrehoztunk egy rendszert rengeteg energiával, azonban a részecskék nem képesek újra elosztani energiáikat, ezért kénytelenek a hegy tetején maradni" - mondta Schneider.

Korábban is alkalmaztak hideg atomokat egyes szubatomi részecskék kölcsönhatásainak szimulálásához. Az új negatív hőmérséklettel azonban olyan szimulált kölcsönhatásokat hozhatnak létre, amikre pozitív hőmérsékleten nem volt lehetőség. "Egy új műszaki eszközt jelentenek a kvantum szimulációk területén" - magyarázta Schneider.

A negatív hőmérsékletnek a kozmológiában is lehet jelentősége. Elvileg a sötét energia, ami megmagyarázná a világegyetem gyorsuló tágulását, negatív nyomást fejt ki, ami arra utal, hogy negatív hőmérséklettel rendelkezik. Schneider jelenleg kozmológusokkal vitatja meg az elképzelést. "Elképesztő kísérleti munka" - mondta a mostani kísérlet mögött meghúzódó elméletet 2005-ben megfogalmazó Allard Mosk, a holland Twente Egyetem fizikusa.

A negatív hőmérsékletű rendszerek egymással és a pozitív energiájú rendszerekkel végbemenő kölcsönhatásainak alaposabb megismerésével soha nem látott hatékonyságú hőerőműveket építhetnénk, ettől azonban még nagyon messze vagyunk, vélekednek a kutatók. "Nem hiszem, hogy mindez azonnal új eszközökkel látna el minket, azonban mélyebb ismereteket kaphatunk arról, mi is a hőmérséklet valójában" - összegzett Mosk.